Calculadora da Lei dos Cossenos

A calculadora da lei dos cossenos da Omni pode ajudar você a resolver um grande número de problemas envolvendo triângulos. Você aprenderá o que é a lei dos cossenos (também conhecida como regra dos cossenos), a fórmula da lei dos cossenos e suas aplicações. Continue lendo para descobrir quando e como usar a lei dos cossenos e conferir as provas dessa lei. Graças a essa calculadora de triângulos, você poderá encontrar rapidamente as propriedades de qualquer triângulo arbitrário.

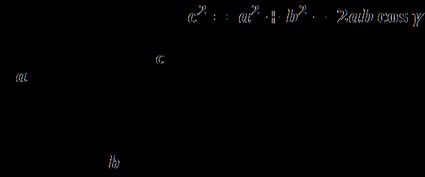
Mas caso você esteja se perguntando o que é a função cosseno, não deixe de acessar a nossa calculadora de cosseno 🇺🇸.

A lei dos cossenos estabelece as seguintes relações entre lados e ângulos de um triângulo:

a² = b² + c² - 2bc ⋅ cos(α)

b² = a² + c² - 2ac ⋅ cos(β)

c² = a² + b² - 2ab ⋅ cos(γ)

Em um triângulo retângulo, o ângulo gama, que é o ângulo entre os lados a e b, é igual a 90°. O cosseno de 90° = 0, portanto, nesse caso especial, a fórmula da lei dos cossenos é reduzida à conhecida equação do Teorema de Pitágoras, ou seja:

a² = b² + c² - 2bc ⋅ cos(90°)

a² = b² + c²

A lei dos cossenos (também conhecida como fórmula do cosseno ou regra do cosseno) descreve a relação entre os comprimentos dos lados de um triângulo e o cosseno de seus ângulos. Ela pode ser aplicada a todos os triângulos, não apenas aos triângulos retângulos. Essa lei generaliza o teorema de Pitágoras, pois permite calcular o comprimento de um dos lados, desde que você saiba o comprimento dos outros lados e o ângulo entre eles.

A lei apareceu no famoso livro Os elementos de Euclides, um tratado matemático que contém definições, postulados e teoremas de geometria. Euclides não a formulou da forma como a aprendemos hoje, pois o conceito de cosseno ainda não havia sido desenvolvido. A versão de Euclides para essa lei é:

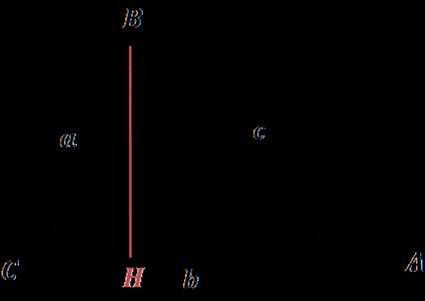
AB² = CA² + CB² − 2 ⋅ CA ⋅ CH (para ângulos agudos)

AB² = CA² + CB² + 2 ⋅ CA ⋅ CH (para ângulos obtusos)

No entanto, podemos reformular o teorema de Euclides facilmente para a versão atual da fórmula do cosseno:

CH = CB ⋅ cos(γ), então AB² = CA² + CB² - 2 ⋅ CA ⋅ (CB ⋅ cos(γ))

Mudando a notação, você obtém a expressão familiar:

c² = a² + b² - 2ab ⋅ cos(γ)

A primeira equação explícita da regra do cosseno foi apresentada pelo matemático persa d'Al-Kashi no século XV. No século XVI, a lei foi popularizada pelo famoso matemático francês Viète antes de receber sua forma final no século XIX.

Você pode manipular as fórmulas da lei dos cossenos para resolver alguns problemas envolvendo triângulos. Confira os seguintes exemplos de aplicação:

1. O terceiro lado de um triângulo, conhecendo dois lados e o ângulo entre eles (LAL):

   • a = √[b² + c² - 2bc ⋅ cos(α)]

   • b = √[a² + c² - 2ac ⋅ cos(β)]

   • c = √[a² + b² - 2ab ⋅ cos(γ)]

2. Os ângulos de um triângulo, conhecendo todos os três lados (LLL):

   • α = arccos [(b² + c² - a²)/(2bc)]

   • β = arccos [(a² + c² - b²)/(2ac)]

   • γ = arccos [(a² + b² - c²)/(2ab)]

3. O terceiro lado de um triângulo, conhecendo dois lados e um ângulo oposto a um deles (LLA):

   • a = b ⋅ cos(γ) ± √[c² - b² ⋅ sen²(γ)]

   • b = c ⋅ cos(α) ± √[a² - c² ⋅ sen²(α)]

   • c = a ⋅ cos(β) ± √[b² - a² ⋅ sen²(β)]

Lembre-se de que conhecer dois lados e um ângulo adjacente pode resultar em dois triângulos distintos, implicando em cenários onde as equações acima possuem uma ou nenhuma solução positiva para o comprimento de um dos lados. Para evitar esse tipo de inconsistência, decidimos implementar os cenários LAL e LLL nesta ferramenta, mas não o LLA.

A lei dos cossenos é uma das leis básicas da trigonometria e é amplamente utilizada em muitos problemas geométricos. Também aplicamos essa lei em muitas ferramentas da Omni, como, por exemplo, na:

• Calculadora de ângulos de um triângulo;
• Calculadora de área de triângulo;
• Calculadora do perímetro de um triângulo; e
• Calculadora de prisma triangular.

Além disso, você pode combinar a calculadora da lei dos cossenos com a calculadora da lei dos senos para resolver outros problemas, por exemplo, encontrar o lado do triângulo, dados dois dos ângulos e um lado (AAL e ALA).

Há muitas formas de provar a equação da lei dos cossenos. Você já leu sobre uma delas, ela vem diretamente da formulação da lei por Euclides e de uma aplicação do teorema de Pitágoras. Você pode escrever as outras provas da lei dos cossenos usando:

1. Trigonometria

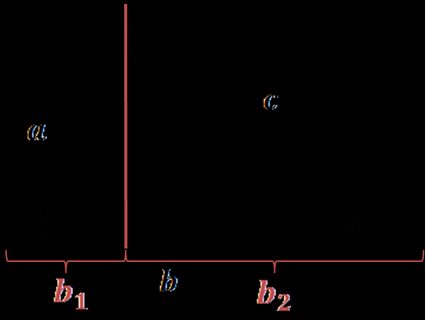
Neste caso, desenhe uma reta referente a altura do triângulo e divida o lado perpendicular a ela em duas partes:

b = b₁ + b₂

A partir das definições de seno e cosseno, b₁ pode ser expresso como a ⋅ cos(γ) e b₂ = c ⋅ cos(α). Portanto:

b = a ⋅ cos(γ) + c ⋅ cos(α) e, multiplicando-o por b, obtemos:

b² = ab ⋅ cos(γ) + bc ⋅ cos(α) (1)

Equações análogas podem ser derivadas para os outros dois lados:

a² = ac ⋅ cos(β) + ab ⋅ cos(γ) (2)

c² = bc ⋅ cos(α) + ac ⋅ cos(β) (3)

Para terminar a prova da lei dos cossenos, você precisa somar as equações (1) e (2) e subtrair (3), ou seja:

a² + b² - c² = ac ⋅ cos(β) + ab ⋅ cos(γ) + bc ⋅ cos(α) + ab ⋅ cos(γ) - bc ⋅ cos(α) - ac ⋅ cos(β)

A simplificação da equação acima fornece uma das formas da regra do cosseno:

a² + b² - c² = 2ab ⋅ cos(γ)

c² = a² + b² - 2ab ⋅ cos(γ)

Ao alterar a ordem em que são adicionadas e subtraídas as equações (1), (2) e (3), você pode derivar as outras fórmulas da lei do cosseno.

2. Fórmula da distância

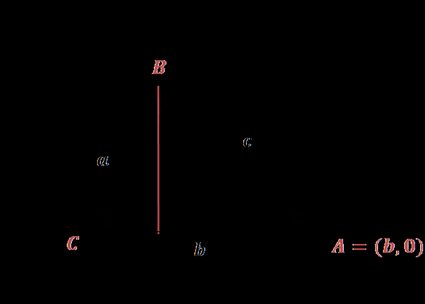
Considere os pontos C = (0,0), A = (b,0), como na figura ao lado.

Para encontrar as coordenadas de B, podemos usar as definições de seno e cosseno:

B = (a ⋅ cos(γ), a ⋅ sen(γ))

A partir da fórmula da distância, determinamos que:

c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a ⋅ cos(γ) - b)² + (a ⋅ sen(γ) - 0)²]

Assim:

c² = a² ⋅ cos(γ)² - 2ab ⋅ cos(γ) + b² + a² ⋅ sen(γ)²

c² = b² + a²(sen(γ)² + cos(γ)²) - 2ab ⋅ cos(γ)

Como a soma dos quadrados do seno e do cosseno é igual a 1, obtemos a fórmula final:

c² = a² + b² - 2ab ⋅ cos(γ)

3. Teorema de Ptolomeu

Outra prova da lei dos cossenos que é relativamente fácil de entender usa o teorema de Ptolomeu:

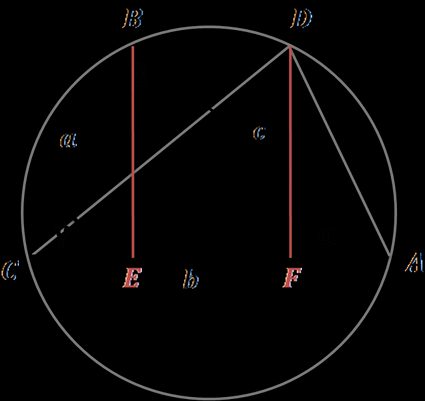
• Suponha que você tenha o triângulo ABC desenhado em uma circunferência, como na figura ao lado.

• Construa o triângulo congruente ADC, onde AD = BC e DC = BA

• As alturas dos pontos B e D dividem a base AC nos pontos E e F, respectivamente. Temos ainda que CE é igual a FA.

• Com base na definição de cosseno, podemos expressar CE como a ⋅ cos(γ).

• Assim, podemos escrever que BD = EF = AC - 2 ⋅ CE = b - 2 ⋅ a ⋅ cos(γ).

• Então, para nosso quadrilátero ADBC, podemos usar o Teorema de Ptolomeu, que informa a relação entre os quatro lados e as duas diagonais. O teorema afirma que, para quadriláteros cíclicos, a soma dos produtos dos lados opostos é igual ao produto das duas diagonais, assim, temos:

  BC ⋅ DA + CA ⋅ BD = AB ⋅ CD

  portanto, no nosso caso:

  a² + b ⋅ (b - 2 ⋅ a ⋅ cos(γ)) + a² = c²

• Após a simplificação, obtemos a fórmula final:

  c² = a² + b² - 2ab ⋅ cos(γ)

A grande vantagem dessas três provas é sua universalidade, elas funcionam para triângulos acutângulos, retângulos e obtusângulos.

4. Usando a lei dos senos
5. Usando a definição de produto escalar 🇺🇸
6. Comparação de áreas
7. Geometria do círculo

As duas últimas provas exigem a distinção entre diferentes tipos de triângulos. A prova baseada em uma definição de produto escalar é mostrada em outro artigo, e a prova que usa a lei dos senos é bastante complicada, portanto, decidimos não reproduzi-la aqui. Se você estiver curioso sobre outras formas de provar a lei dos cossenos, confira este artigo da Wikipedia.

1. Comece formulando o problema. Por exemplo, você pode conhecer dois lados do triângulo e o ângulo entre eles e está procurando o lado restante.

2. Insira os valores conhecidos nos campos apropriados desta calculadora. Lembre-se de verificar novamente a imagem do triângulo, para saber se você indicou os lados e os ângulos com os símbolos corretos.

3. Veja nossa calculadora de lei dos cossenos realizar todos os cálculos para você!

Se a sua tarefa for encontrar os ângulos de um triângulo dados os três lados, tudo o que você precisa fazer é usar as fórmulas da regra do cosseno abaixo:

α = arccos [(b² + c² - a²)/(2bc)]
β = arccos [(a² + c² - b²)/(2ac)]
γ = arccos [(a² + b² - c²)/(2ab)]

Vamos calcular um dos ângulos. Considere que a = 4 cm, b = 5 cm e c = 6 cm. Usaremos a primeira equação para encontrar α:

α = arccos [(b² + c² - a²)/(2bc)]

= arccos [(5² + 6² - 4²)/(2 ⋅ 5 ⋅ 6)]

= arccos [(25 + 36 - 16)/60]

= arccos [(45/60)] = arccos [0,75]

α = 41,41°

Você pode calcular o segundo ângulo a partir da segunda equação de forma análoga, e o terceiro ângulo você pode encontrar sabendo que a soma dos ângulos em um triângulo é igual a 180° (π).

Se você quiser economizar tempo, digite os comprimentos dos lados em nossa calculadora da lei dos cossenos. Nossa ferramenta é uma aposta segura! Basta que você siga os passos abaixo:

1. Escolha a opção apropriada para os valores fornecidos. Precisamos escolher a segunda opção, ou seja, LLL (3 lados).

2. Digite os dados conhecidos. Neste caso temos: a = 4 cm, b = 5 cm e c = 6 cm.

3. A calculadora mostra o resultado! No nosso exemplo, os ângulos são iguais a α = 41,41°, β = 55,77° e γ = 82,82°.

Depois dessa explicação, temos certeza de que você entende o que é a lei do cosseno e quando usá-la. Experimente a nossa ferramenta, resolva alguns exercícios e lembre-se de que a prática ajudará você a fixar o conteúdo.