Calculadora de Distância

Você já quis calcular a distância de um ponto a outro ou a distância entre duas cidades, por exemplo? Você já se perguntou qual é a definição de distância? Aqui você encontrará todas essas respostas, além de uma explicação detalhada de como calcular a distância entre dois objetos quaisquer no plano 2D. Como bônus, temos um tópico fascinante sobre como percebemos as distâncias. Confira também a calculadora de diferença percentual da Omni. Temos certeza de que você vai adorar!

Você prefere assistir a ler? Aprenda tudo o que você precisa em 90 segundos com este vídeo que fizemos para você:

Antes de falarmos sobre como calcular distâncias, provavelmente deveríamos esclarecer o que é uma distância. O significado mais comum é o espaço 1D entre dois pontos. Essa definição é uma maneira de dizer o que quase todos nós pensamos sobre distância intuitivamente, mas não é a única maneira de falar sobre distância. Você verá nas seções a seguir como o conceito de distância pode ser estendido para além do comprimento. Falaremos inclusive sobre a descoberta por trás da teoria da relatividade de Einstein!

Se mantivermos a definição geométrica de distância, ainda teremos de definir em que tipo de espaço estamos trabalhando (1D, 2D ou 3D). Na maioria dos casos, você provavelmente está falando de três dimensões ou menos, pois isso é tudo o que podemos imaginar sem que nossos cérebros explodam. Para esta calculadora, vamos nos concentrar apenas na distância 2D (com a 1D incluída como um caso especial). Se você estiver procurando a distância 3D entre 2 pontos, recomendamos que use a calculadora de distância tridimensional 🇺🇸 da Omni, criada especificamente para essa finalidade.

Para encontrar a distância entre dois pontos, a primeira coisa que você precisa é de dois pontos, obviamente. Esses pontos são descritos por suas coordenadas no espaço. Para cada ponto no espaço 2D, precisamos de duas coordenadas que sejam exclusivas desse ponto. Se você quiser encontrar a distância entre dois pontos no espaço 1D, ainda poderá usar essa calculadora simplesmente definindo uma das coordenadas como sendo a mesma para ambos os pontos. Como esse é um caso muito especial, a partir de agora falaremos apenas sobre distância em duas dimensões.

Se você quiser ser mais exato e preciso, a próxima etapa é definir o tipo de espaço em que está trabalhando. Não se assuste! Isso é mais fácil do que você pensa. Se você não sabe em que espaço está trabalhando ou se nem sabia que havia mais de um tipo de espaço, você provavelmente está trabalhando no espaço euclidiano. Já que esse é o espaço “padrão” no qual fazemos quase todas as operações geométricas e é o espaço que definimos para a calculadora operar. Vamos nos aprofundar um pouco mais no espaço euclidiano, o que é, quais propriedades ele tem e por que é tão importante?

O espaço euclidiano ou geometria euclidiana é o que todos nós normalmente pensamos ser o espaço 2D antes de recebermos qualquer treinamento matemático profundo em qualquer um desses aspectos. No espaço euclidiano, a soma dos ângulos de um triângulo é igual a 180º e os quadrados sempre têm todos os seus ângulos iguais a 90º. Isso é algo que todos nós tomamos como certo, mas isso não é verdade em todos os espaços. Também não devemos confundir o espaço euclidiano com espaços multidimensionais. O espaço euclidiano pode ter quantas dimensões você quiser, desde que haja um número finito delas, e elas ainda obedecem às regras euclidianas.

Não queremos entediá-lo com definições matemáticas sobre o que é um espaço e o que torna o espaço euclidiano único, pois isso seria muito complicado para explicar em uma simples calculadora de distância. Entretanto, podemos tentar dar alguns exemplos de outros espaços comumente usados, que podem ajudar você a entender por que o espaço euclidiano não é o único tipo de espaço. Além disso, você poderá entender por que não nos preocuparemos em calcular distâncias em outros espaços.

O primeiro exemplo que apresentamos pode ser um pouco obscuro, no entanto, é muito importante, que é o espaço de Minkowski. Esperamos que você possa nos desculpar, já que somos físicos. O motivo pelo qual o selecionamos é porque ele é muito comum na física, em particular, é usado na teoria da relatividade, na relatividade geral e até mesmo na teoria quântica de campos. Esse espaço é muito semelhante ao espaço euclidiano, mas difere dele em uma característica crucial: a adição do produto escalar.

Tanto o espaço euclidiano quanto o espaço de Minkowski são o que os matemáticos chamam de espaço plano. Isso significa que o próprio espaço tem propriedades planas; por exemplo, a distância mais curta entre dois pontos quaisquer é sempre uma linha reta entre eles (verifique a calculadora de interpolação linear 🇺🇸 da Omni). No entanto, há outros tipos de espaços matemáticos chamados espaços curvos nos quais o espaço é intrinsecamente curvo e a menor distância entre dois pontos não é uma linha reta.

Esse espaço curvo é difícil de imaginar em 3D, mas em 2D podemos imaginar que, em vez de termos uma área plana, temos um espaço 2D, por exemplo, curvado no formato da superfície de uma esfera. Nesse caso, coisas muito estranhas acontecem. A distância mais curta de um ponto a outro não é uma linha reta, pois qualquer linha nesse espaço é curva devido à curvatura intrínseca do espaço. Outra característica muito estranha desse espaço é que algumas retas paralelas 🇺🇸 de fato se encontram em algum ponto. Você pode tentar entender isso pensando nas chamadas linhas de longitude que dividem a Terra em vários fusos horários e se cruzam nos polos.

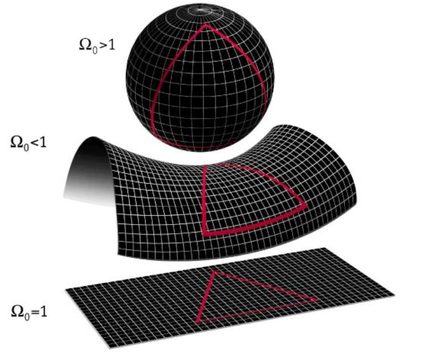
É importante observar que isso é conceitualmente MUITO diferente de uma mudança de coordenadas. Quando pegamos as coordenadas $x, y, z$ padrão e as convertemos em coordenadas polares, cilíndricas ou mesmo esféricas, ainda assim estaremos no espaço euclidiano. Quando falamos de espaço curvo, estamos falando de um espaço muito diferente em termos de suas propriedades intrínsecas. Em coordenadas esféricas, você ainda pode ter uma linha reta e a distância ainda é medida em uma linha reta, mesmo que isso seja muito difícil de expressar em números.

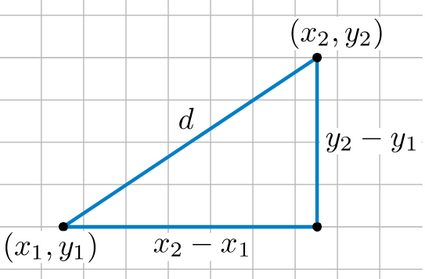
Voltando ao espaço euclidiano, agora podemos apresentar a você a fórmula da distância que prometemos no início. A fórmula da distância é:

Essa fórmula está relacionada ao teorema de Pitágoras, que afirma que $a^2+b^2=c^2$. Aqui, $a$ e $b$ são os catetos de um triângulo retângulo e $c$ é a hipotenusa. Suponha que dois pontos, $(x_1, y_1)$ e $(x_2, y_2)$, sejam as coordenadas dos pontos finais da hipotenusa. Então, $(x_2 - x_1)^2$ na equação da distância corresponde a $a^2$ e $(y_2 - y_1)^2$ corresponde a $b^2$. Como $c = \sqrt{a^2 + b^2}$, você pode ver por que isso é apenas uma extensão do teorema de Pitágoras.

A fórmula da distância que acabamos de ver é a fórmula da distância euclidiana padrão, mas se você pensar bem, ela pode parecer um pouco limitada. Muitas vezes não queremos encontrar apenas a distância entre dois pontos. Às vezes, queremos calcular a distância de um ponto a uma reta ou a um círculo. Nesses casos, primeiro precisamos definir qual ponto dessa reta ou circunferência usaremos para o cálculo da distância e, em seguida, usar a fórmula de distância que vimos acima.

É aqui que o conceito de reta perpendicular se torna crucial. Você pode checar o conceito e alguns exemplos na calculadora de retas perpendiculares 🇺🇸 da Omni. A distância entre um ponto e um objeto contínuo é definida por meio da perpendicularidade. Do ponto de vista geométrico, a primeira etapa para medir a distância de um ponto a outro é criar uma linha reta entre os dois pontos e, em seguida, medir o comprimento desse segmento. Quando medimos a distância de um ponto a uma reta, a pergunta se torna "qual das muitas retas possíveis devo traçar?". Nesse caso, a resposta é: A reta do ponto que é perpendicular à primeira reta. Essa distância será zero no caso em que o ponto for uma parte da reta. Para esses casos 1D, só podemos considerar a distância entre os pontos, uma vez que a reta representa todo o espaço 1D.

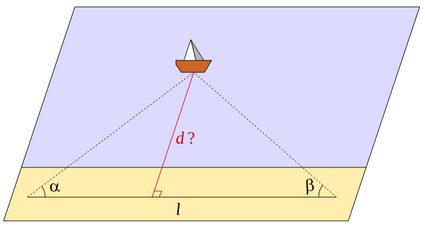
Isso impõe restrições sobre como calcular distâncias em algumas instâncias geométricas interessantes. Por exemplo, poderíamos redefinir o conceito de altura de um triângulo para ser simplesmente a distância de um vértice até o lado oposto do triângulo. Nesse caso, a área do triângulo também é redefinida em termos de distância, já que a área é uma função da altura do triângulo.

Dêmos uma olhada em alguns exemplos no espaço 2D. Para calcular a distância entre um ponto e uma linha reta, você pode seguir o passo a passo (calcular o segmento perpendicular à linha desde a reta até o ponto e calcular seu comprimento) ou pode simplesmente usar esta “prática” equação:

onde a reta é dada por $Ax+By+C = 0$ e o ponto é definido por $(x_1, y_1)$.

O único problema aqui é que uma linha reta é geralmente dada como $y=mx+b$, portanto, precisaríamos converter essa equação para a forma mostrada anteriormente:

Assim, podemos ver que $A=m$, $B=-1$ e $C=b$. Isso deixa a equação anterior com os seguintes valores:

Para saber a distância entre duas retas, basta calcular o comprimento do segmento que vai de uma à outra e é perpendicular a ambas. Mais uma vez, há uma fórmula simples para nos ajudar:

se as retas forem $A_1x+B_1y+C_1=0$ e $A_2x+B_2y+C_2=0$. Podemos convertê-las para a forma da equação reduzida da reta, obtendo:

para as retas $y=m_1x+b_1$ e $y=m_2x+b_2$.

Observe que ambas as retas precisam ser paralelas, pois, caso contrário, elas se tocariam em algum ponto e sua distância seria $d=0$. Essa é a razão pela qual as fórmulas omitem a maioria dos subscritos, pois para as retas paralelas: $A_1=A_2=A$ e $B_1=B_2=B$, enquanto na forma de equação reduzida da reta as retas paralelas são aquelas para as quais $m_1=m_2=m$.

Como mencionamos anteriormente, distância pode significar muitas coisas, e é por isso que fornecemos algumas opções diferentes para você nessa calculadora. Você pode calcular a distância entre um ponto e uma reta, a distância entre duas retas (elas sempre precisam ser paralelas) ou a distância entre pontos no espaço. Quando se trata de calcular as distâncias entre dois pontos, você tem a opção de fazer isso em 1, 2, 3 ou até 4 dimensões. Sim, 4 dimensões parece assustador, mas você não precisa usar essa opção. E você sempre pode aprender mais sobre isso lendo algum artigo interessante e brincando com a calculadora. Temos certeza que você não quebrará a internet ou o universo.

Também adicionamos a possibilidade de definir 3 pontos diferentes no espaço, a partir dos quais você obterá os 3 pares de distâncias entre eles; portanto, se você tiver mais de dois pontos, isso economizará seu tempo. O número de dimensões em que você estiver trabalhando determinará o número de coordenadas que descrevem um ponto, e é por isso que, à medida que você aumentar o número de dimensões, a calculadora solicitará mais valores de entrada.

Embora o uso da calculadora seja muito simples, ainda assim decidimos incluir uma solução passo a passo. Dessa forma, você pode se familiarizar com a fórmula da distância e como usá-la (como se estivéssemos na década de 1950 e a internet ainda não existisse). Agora dêmos uma olhada em um exemplo prático: como encontrar a distância entre dois pontos em 2D.

Suponha que você tenha duas coordenadas, $(3, 5)$ e $(9, 15)$, e queira calcular a distância entre elas. Para calcular a distância 2D entre esses dois pontos, siga estas etapas:

1. Insira os valores na fórmula: $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
2. Subtraia os valores entre parênteses.
3. Eleve ao quadrado as duas quantidades entre parênteses.
4. Some os resultados.
5. Tire a raiz quadrada.
6. Use a calculadora de distância da Omni para verificar seus resultados.

Trabalhando com o exemplo manualmente, você obtém:

que é igual a aproximadamente $11,66$. Observe que, ao tirar a raiz quadrada, você obterá um resultado positivo e um negativo, mas como está lidando com distância, apenas o resultado positivo interessa. A calculadora realizará esses cálculos passo a passo para fornecer o resultado nos formatos exato e aproximado.

Vamos dar uma olhada em uma das aplicações da calculadora de distância. Suponha que você esteja viajando entre as cidades A e B e que a única parada seja na cidade C, com uma rota de A a B perpendicular à rota de B a C. Podemos determinar a distância de A a B e, conhecendo o preço da gasolina, determinar o custo do combustível, o combustível usado e o custo por pessoa durante a viagem. A calculadora de combustível, também disponível no nosso site, pode facilitar isso para você.

A dificuldade aqui é calcular as distâncias entre as cidades com precisão. Uma linha reta (como a que usamos nesta calculadora) pode ser uma boa aproximação, mas pode ser bastante incorreta se a rota que você está tomando não for direta, mas tiver algum desvio, talvez para evitar montanhas ou passar por outra cidade. Nesse caso, basta usar o Google Maps ou qualquer outra ferramenta que calcule a distância ao longo de um caminho e não apenas a distância de um ponto a outro em linha reta.

Nossa calculadora fornece medições e previsões adequadas para distâncias entre objetos, mas não necessariamente para o comprimento de um caminho. Com isso em mente, ainda há vários cenários em que você pode estar interessado na distância entre objetos, independentemente do caminho que teria de percorrer. Um exemplo disso é a distância entre objetos astronômicos.

Quando olhamos para uma distância dentro da Terra, é difícil ir longe sem esbarrar em alguns problemas, desde a curvatura intrínseca desse espaço (devido ao fato de a curvatura da Terra ser diferente de zero) até o limite na distância máxima entre dois pontos na Terra. É por isso, e também porque existe um universo inteiro além da Terra, que as distâncias no universo são de grande interesse para muitas pessoas. Como não temos meios adequados para viagens interplanetárias, muito menos para viagens interestelares, vamos nos concentrar por enquanto na distância euclidiana real de alguns objetos celestes. Por exemplo, a distância da Terra ao Sol ou a distância da Terra à Lua.

Essas distâncias estão além do imaginável para nossos cérebros. Temos dificuldade para compreender o tamanho de nosso planeta, sem falar no vasto e infinito universo. Isso é tão difícil que precisamos usar notação científica ou anos-luz como unidade de distância para comprimentos tão longos. As viagens mais longas que você pode fazer na Terra têm apenas alguns milhares de quilômetros, enquanto a distância da Terra à Lua, o objeto astronômico mais próximo de nós, é de 384.000 km. Além disso, a distância até nossa estrela mais próxima, ou seja, a distância da Terra ao Sol, é de 150.000.000 km ou pouco mais de 8 minutos-luz.

Quando você compara essas distâncias com a distância até nossa segunda estrela mais próxima (Alpha Centauri), que é de 4 anos-luz, de repente elas começam a parecer muito menores. Se você quiser fazer uma comparação ainda mais simples, podemos pensar em um voo de São Paulo a Sydney (Austrália), que normalmente leva mais de 20 horas e cerca de 13.000 km, e compará-lo com o tamanho do universo observável, que é de cerca de 46.600.000.000 anos-luz**!

Aqui, nós inadvertidamente levantamos um ponto fascinante, que é o fato de medirmos as distâncias não em comprimento, mas em tempo. Assim, estendemos a noção de distância para além de seu sentido geométrico. Exploraremos essa possibilidade na próxima seção ao falarmos sobre a importância e a utilidade da distância além do sentido puramente geométrico. Esse é um caminho muito interessante a ser seguido e é inspirado principalmente pela necessidade filosófica de estender todos os conceitos em um significado universal, bem como pela teoria física óbvia a ser mencionada, ao falar sobre permutações do espaço e do tempo, ou qualquer outra variável que possa ser medida.

Normalmente, o conceito de distância se refere à distância geométrica euclidiana e está vinculado ao comprimento. Entretanto, você pode estender a definição de distância como apenas a diferença entre duas coisas, e então um mundo de possibilidades se abre. De repente, você pode decidir qual é a melhor maneira de medir a distância entre duas coisas e colocá-la em termos da quantidade. Um passo muito simples é pensar na distância entre dois números, que não é nada mais do que a diferença 1D entre esses números. Para obtê-la, basta subtrair um do outro e o resultado será a diferença, ou seja, a distância.

Poderíamos saltar dessa distância numérica para, por exemplo, a diferença ou distância em termos de diferença percentual, o que, em alguns casos, pode proporcionar uma maneira melhor de comparação. Esse ainda é apenas um nível de abstração no qual simplesmente removemos as unidades de medida. Mas e se você usasse unidades completamente diferentes?

Ao ampliar o conceito de distância para significar algo mais próximo de diferença, podemos calcular a diferença entre duas temperaturas ou outra quantidade relacionada, como pressão. Mas não precisamos chegar a extremos, vamos ver como dois pontos podem ser separados por uma distância diferente, dependendo das suposições feitas. Voltando ao exemplo da distância dirigida, poderíamos medir a distância da viagem em tempo, em vez de comprimento. Nesse caso, precisamos de uma suposição para permitir essa transposição, por exemplo, uma mudança no meio de transporte.

Há uma grande diferença entre o tempo gasto para percorrer 10 km de avião e o tempo gasto dirigindo um carro. Às vezes, porém, a suposição é clara e implicitamente aceita, como quando medimos a distância de um raio em tempo, que depois convertemos em comprimento. Isso traz à tona um ponto interessante: o fator de conversão entre distâncias em tempo e comprimento é o que chamamos de “velocidade” ou “rapidez” (lembre-se de que não são exatamente a mesma coisa). A verdade é que essa velocidade não precisa ser constante, como exemplificado por movimentos acelerados. Alguns exemplos são o movimento de um objeto em queda livre, que está sob força gravitacional. Outros exemplos são a força de frenagem, também conhecida como força de arrasto, ou ainda a força de um impacto, como em acidentes de carro.

Outro lugar em que você pode encontrar unidades estranhas de distância é na física do estado sólido, em que a distância que uma partícula percorre dentro de um material é frequentemente expressa como uma média de interações ou colisões. Essa distância está vinculada ao comprimento usando o caminho livre médio, que é a distância média (em comprimento) que uma partícula percorre entre as interações. Se quisermos ser ainda mais diferente, podemos pensar na distância entre o valor presente e o valor futuro de algo, como um carro, por exemplo.

No entanto, não queremos fazer o cérebro de ninguém explodir, portanto, por favor, não pense muito sobre isso. Basta que você pegue esta calculadora e a use para calcular a distância baseada em comprimento no espaço 2D. Você sempre pode voltar a essa visão filosófica sobre distâncias se ficar entediado!

Para encontrar a distância entre dois pontos, usaremos a fórmula da distância: √[(x₂ - x₁)² + (y₂ - y₁)²]:

1. Obtenha as coordenadas de ambos os pontos no espaço.
2. Subtraia as coordenadas x de um ponto e outro e faça o mesmo com os componentes y.
3. Eleve os dois resultados ao quadrado separadamente.
4. Some os valores que você obteve na etapa anterior.
5. Encontre a raiz quadrada do resultado acima.

Se achar que isso é muito trabalhoso, você pode simplesmente usar a calculadora de distância da Omni

A distância não é um vetor. A distância entre pontos é uma quantidade escalar, o que significa que ela é definida apenas por seu valor. No entanto, o deslocamento é um vetor com valor e direção. Portanto, a distância entre A e B é a mesma que a distância de B a A, mas o deslocamento é diferente dependendo da ordem.

Click é um termo em inglês, muito utilizado para substituir o termo quilômetro, e equivale a 0,62 milhas. Na verdade, é escrito com "k" (Klick), pois é derivado da palavra quilômetro. É comumente usado por militares e motociclistas.

A fórmula da distância é: √[(x₂ - x₁)² + (y₂ - y₁)²]. Isso funciona para quaisquer dois pontos no espaço 2D com coordenadas (x₁, y₁) para o primeiro ponto e (x₂, y₂) para o segundo ponto. Você pode memorizá-lo facilmente se perceber que é o teorema de Pitágoras e a distância é a hipotenusa, e os comprimentos dos catetos são a diferença entre os componentes x e y dos pontos.

A distância de um vetor é sua magnitude. Se você conhece seus componentes:

1. Pegue cada um dos componentes do vetor e eleve-os ao quadrado.
2. Some-os.
3. Encontre a raiz quadrada do resultado anterior.
4. Bom trabalho!

Se você souber sua representação polar, ela será um número e um ângulo. Esse número é a magnitude do vetor, que é sua distância.

A unidade SI de distância é o metro, abreviado como "m". Um metro equivale a aproximadamente 3,28 pés. Outras unidades comuns no Sistema Internacional de unidades são o centímetro (um centésimo de metro, ou 0,39 polegadas) e o quilômetro (mil metros ou 0,62 milhas), entre outras.

A distância de A a B é o comprimento da linha reta que vai de A a B. A distância de B a A é a mesma que a distância de A a B porque a distância é escalar

A distância é uma medida no espaço unidimensional. A distância entre dois pontos é o comprimento mais curto do espaço 1D entre eles. Se você dividir a distância pelo tempo, obterá a velocidade, que tem dimensões de espaço ao longo do tempo.

Um ano-luz é uma medida de distância. É 9,461×10¹² quilômetros, que é a distância percorrida por um raio de luz em um vácuo perfeito no período de um ano.

Com a velocidade e o tempo de movimento de um objeto, você pode calcular a distância:

1. Certifique-se de que a velocidade e o tempo tenham unidades compatíveis (km/h e horas, m/s e segundos...).
2. Se não forem, converta-os para as unidades necessárias.
3. Multiplique a velocidade pelo tempo.
4. O resultado deve ser a distância percorrida na unidade de comprimento que você estava usando!