Kalkulator wysokości trójkąta
Jeśli szukasz łatwego w obsłudze narzędzia do obliczania wysokości w dowolnym trójkącie, jesteś we właściwym miejscu — Omni kalkulator wysokości trójkąta jest narzędziem dla ciebie.
Niezależnie od tego, czy szukasz wzorów na wysokość trójkąta dla szczególnych typów trójkąta, takich jak trójkąty prostokątne, równoboczne lub równoramienne, czy też interesuje cię dowolne trójkąty, nasz kalkulator jest sprawdzonym rozwiązaniem — może obliczyć nie tylko wysokość trójkąta, ale też także jego boki, kąty, obwód i pole powierzchni. Nie czekaj dłużej, spróbuj!
Jeśli nadal zastanawiasz się nad wzorem na wysokość trójkąta równobocznego lub nie wiesz, jak obliczyć wysokość bez znajomości pola powierzchni, odpowiedź znajdziesz poniżej.
Czym jest wysokość trójkąta?
Każdy bok trójkąta może być jego podstawą, a z każdego wierzchołka możesz narysować prostą prostopadłą do podstawy — będzie to wysokość trójkąta. Każdy trójkąt ma zatem trzy wysokości. Rysowanie wysokości jest też nazywane opuszczaniem wysokości z danego wierzchołka.
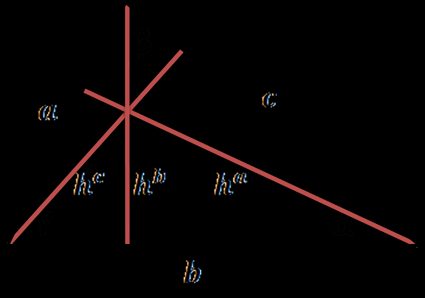
Jak obliczyć wysokość trójkąta? Wzory
Istnieje wiele sposobów na obliczanie wysokości trójkąta. Najpopularniejszym jest wykorzystanie pola powierzchni trójkąta, ale są też inne wzory:
-
Dane jest pole trójkąta.
Dobrze znane równanie na pole trójkąta można przekształcić we wzór na wysokość trójkąta:
-
, gdzie jest podstawą, jest wysokością;
-
Zatem .
Ale jak znaleźć wysokość trójkąta bez znajomości pola? Najpopularniejsze sytuacje to:
-
-
Dane są boki trójkąta
Korzystając z równania zwanego wzorem Herona, możesz obliczyć pole znając boki trójkąta. Następnie, gdy już znasz pole, możesz użyć podanego wyżej równania, aby dowiedzieć się, jaka jest wysokość trójkąta:
Wzór Herona:
Zatem:
Możesz dowiedzieć się więcej o tym równaniu w naszym kalkulatorze wzoru Herona 🇺🇸.
-
Dane są dwa boki i kąt między nimi
Użyj trygonometrii lub innego wzoru do wyznaczenia pola trójkąta:
(lub lub , w zależności od tego, które boki są znane):
Jeśli badany trójkąt jest jakimś szczególnym typem trójkąta, to zainteresują cię kolejne wzory na wysokość. Uproszczone wersje ogólnych równań są łatwiejsze do zapamiętania i zastosowania.
Jak znaleźć wysokość trójkąta równobocznego?
Trójkąt równoboczny to trójkąt, którego wszystkie trzy boki są równej długości, a wszystkie trzy kąty są równe . Wszystkie trzy wysokości mają taką samą długość, którą można obliczyć na podstawie wzoru:
- , gdzie jest bokiem trójkąta.
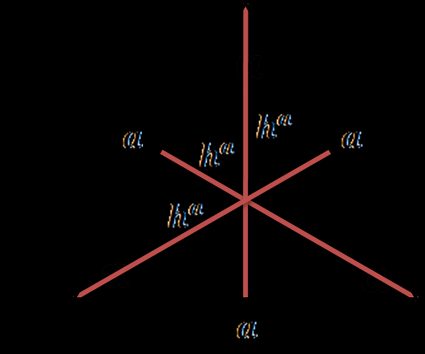
W trójkącie równobocznym wysokości, dwusieczne kątów, środkowe i symetralne boków pokrywają się.
Jeśli interesują cię wzory na pole i obwód, odwiedź nasz kalkulator trójkąta równobocznego .
Jak znaleźć wysokość trójkąta równoramiennego?
Trójkąt równoramienny to trójkąt o dwóch bokach równej długości. Wysokości opuszczone na ramiona są równej długości, ale wysokość opuszczona na podstawę może mieć inną długość. Wzór na wysokość opuszczoną na podstawę jest następujący:
-
, gdzie jest ramieniem trójkąta, a jest podstawą. Wzór ten wyprowadzamy z twierdzenia Pitagorasa.
-
Wysokości opuszczone na ramiona można obliczyć następująco:
Wzór na pole powierzchni:
Trygonometria:
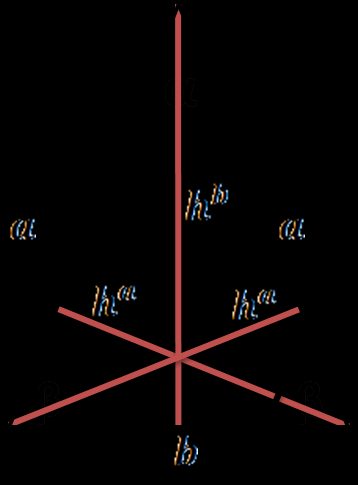
Aby poznać wzory na pole powierzchni i obwód tego typu trójkąta, odwiedź nasz kalkulator trójkąta równoramiennego.
Jak znaleźć wysokość trójkąta prostokątnego?
Trójkąt prostokątny to trójkąt o jednym kącie równym . Dwie wysokości są łatwe do znalezienia, ponieważ dwa boki trójkąta są prostopadłe: jeśli jeden z nich potraktujemy jako podstawę, to drugi będzie wysokością. Trzecią wysokość trójkąta można obliczyć ze wzoru:

Jeśli interesują cię wzory na pole i obwód tego trójkąta, zajrzyj do naszego kalkulatora trójkąta prostokątnego.
Jak znaleźć wysokość trójkąta za pomocą Omni kalkulatora wysokości trójkąta?
Jesteśmy niemal pewni, że po przeczytaniu naszych wyjaśnień już rozumiesz, jak znaleźć wysokość trójkąta bez znajomości pola i że potrafisz powiedzieć, czym w ogóle jest wysokość trójkąta. Przyjrzyjmy się jeszcze prostemu przykładowi, aby zaprezentować elastyczność naszego narzędzia:
- Wybierz typ trójkąta. Załóżmy, że chcemy obliczyć wysokość trójkąta różnobocznego, więc nie zmieniamy domyślnej opcji.
- Wprowadź znane wartości. Mogą to być trzy boki lub dwa boki i kąt. Pozostańmy przy pierwszej opcji: , , .
- Kalkulator wysokości trójkąta wyświetlił wszystkie trzy wysokości — są one równe , , oraz . Co więcej, kalkulator pokazał nam też wszystkie kąty trójkąta, jego pole i obwód!
Czyż to nie wspaniałe?
FAQs
Jak znaleźć wysokość trójkąta, jeśli wszystkie boki są równe?
Aby określić wysokość trójkąta równobocznego:
- Zapisz długość boku trójkąta.
- Pomnóż ją przez
√3 ≈ 1,73. - Podziel wynik przez
2. - To wszystko! Wynik jest wysokością twojego trójkąta!
Czy wszystkie wysokości trójkąta są równe?
Ogólnie nie, każda wysokość trójkąta może mieć inną długość. Jednakże, jeśli wszystkie trzy wysokości mają równe długości, to ten trójkąt jest równoboczny, czyli wszystkie jego boki są również równe (ale nie są równe wysokościom!).
Jak znaleźć wysokość trójkąta o podanych kątach?
Nie można określić wysokości trójkąta, biorąc pod uwagę tylko jego kąty wewnętrzne. Dzieje się tak, bo istnieje nieskończenie wiele trójkątów o tych samych kątach, a wysokości w każdym z tych nich mają inną długość!
Jak znaleźć wysokość trójkąta prostokątnego?
Każdy z prostopadłych boków (przyprostokątnych) w trójkącie prostokątnym jest jego wysokością. Aby obliczyć trzecią wysokość h3, skorzystaj ze wzoru na pole powierzchni:
½ ⋅ Przyprostokątna1 ⋅ Przyprostokątna2 = Pole = ½ ⋅ Przeciwprostokątna ⋅ h3
W rezultacie:
h3 = Przyprostokątna1 ⋅ Przyprostokątna2 / Przeciwprostokątna
Jaka jest najmniejsza wysokość trójkąta 3 4 5?
Odpowiedzią jest 2,4. Aby uzyskać ten wynik, zwróć uwagę, że pole powierzchni wynosi Pole = ½ ⋅ 3 ⋅ 4 = 6.
Wiemy też, że Pole = ½ ⋅ Przeciwprostokątna ⋅ Najkrótsza wysokość.
Ponieważ Przeciwprostokątna = 5 i Pole = 6, otrzymujemy Najkrótsza wysokość = 2 ⋅ Pole / Przeciwprostokątna = 2 ⋅ 6 / 5 = 2,4.