Kalkulator trójkąta prostokątnego

Kalkulator trójkąta prostokątnego pomoże ci znaleźć długości boków lub pole powierzchni każdego trójkąta prostokątnego. Z naszym narzędziem nauczysz się również jak znaleźć pole powierzchni trójkąta prostokątnego oraz dowiesz się o praktycznych zastosowaniach trójkątów prostokątnych.

Na początek wyjaśnijmy, czym jest trójkąt prostokątny. Definicja jest bardzo prosta i może nawet wydawać się oczywista dla tych, którzy już ją znają — trójkąt prostokątny to trójkąt, w którym jeden i tylko jeden z kątów ma dokładnie 90°. Pozostałe dwa kąty są oczywiście mniejsze niż kąt prosty, ponieważ suma wszystkich kątów w trójkącie wynosi zawsze 180°.

W trójkącie prostokątnym definiujemy boki w szczególny sposób. Bok przeciwny do kąta prostego jest zawsze najdłuższy w trójkącie i nazywany jest przeciwprostokątną (ponieważ znajduje się naprzeciw kąta prostego). Pozostałe dwa boki nazywane są przyprostokątnymi (ponieważ są umiejscowione przy kącie prostym). Związek między przeciwprostokątną a przyprostokątnymi nie jest skomplikowany, o czym przekonacie się dalej, gdy omówimy twierdzenie Pitagorasa.

Jeśli potrzebujesz obliczyć długość przeciwprostokątnej, możesz to zrobić z tym kalkulatorem trójkąta prostokątnego. Jednak możesz też użyć, opracowanego przez nas w Omni, dedykowanego narzędzia: kalkulatora przeciwprostokątnej. Przeciwprostokątna jest bokiem przeciwnym do kąta prostego, którego długość możesz odnaleźć za pomocą twierdzenia Pitagorasa. W trójkącie prostokątnym o przyprostokątnych a i b oraz o przeciwprostokątnej c, twierdzenie Pitagorasa mówi, że: a² + b² = c².

Aby znaleźć c, należy spierwiastkować obie strony, aby otrzymać c = √(b²+a²). Takie rozszerzenie twierdzenia Pitagorasa możemy nazwać wzorem na przeciwprostokątną. Doskonałym narzędziem do obliczania przeciwprostokątnej jest również kalkulator twierdzenia Pitagorasa.

Spójrzmy teraz na praktyczny przykład tego, co trzeba zrobić, aby obliczyć przeciwprostokątną trójkąta prostokątnego bez użycia specjalnego kalkulatora dostępnego w Omni:

1. Ustal wartości a i b.
2. Podnieś je do kwadratu: a² i b².
3. Zsumuj podniesione do kwadratu wartości: a² + b².
4. Oblicz pierwiastek kwadratowy z otrzymanego wyniku.
5. Pierwiastkowanie da dwa wyniki — dodatni i ujemy. Jako że chcemy znaleźć długość, zignoruj wynik ujemny.
6. Otrzymana wartość jest długością przeciwprostokątnej c.

Jak wyglądałby ten proces gdybyśmy używali jednego z kalkulatorów z Omni?

1. Wprowadź do kalkulatora wartości a i b.
2. Natychmiast otrzymasz wartość c.
3. Dodatkowo, dowiesz się jakie pole powierzchni ma trójkąt.

Wiemy już, że używając kalkulatora trójkąta prostokątnego, obliczenie pola powierzchni jest bardzo łatwe. W Omni Calculator stworzyliśmy również kalkulator specjalnie do tego zaprojektowany: kalkulator pola powierzchni trójkąta prostokątnego 🇺🇸. Sprawdźmy teraz, jak obliczyć pole trójkąta prostokątnego bez takiego narzędzia.

Metoda na znalezienie pola trójkąta prostokątnego jest dość prosta. Wszystko, czego potrzebujesz to długości podstawy i wysokości. W trójkącie prostokątnym podstawa i wysokość to dwa boki, które tworzą kąt prosty. Ponieważ pomnożenie tych dwóch wartości dałoby pole odpowiedniego prostokąta, a trójkąt jest jego połową, wzór brzmi:

pole powierzchni = ½ × podstawa × wysokość.

Jeśli nie znasz długości podstawy lub wysokości, możesz je odnaleźć, korzystając z twierdzenia Pitagorasa. Aby sprawdzić swoje obliczenia lub obliczyć pole trójkątów o dłuższych, lub dziesiętnych długościach boków, wypróbuj kalkulator trójkątów prostokątnych.

Co jeszcze można obliczyć znając właściwości trójkątów prostokątnych? Boki trójkąta mają pewien gradient lub nachylenie. Wzór na nachylenie to:

Nachylenie = (y₂ - y₁)/(x₂ - x₁).

Na przykład, jeśli mamy współrzędne (1,-6) i (4,8) to nachylenie odcinka wynosi (8 + 6)/(4 - 1) = 14/3. Łatwym sposobem na określenie, czy trójkąt jest prosty, gdy znasz tylko jego współrzędne, jest sprawdzenie, czy pomnożone nachylenia dwóch dowolnych linii są równe -1.

Przy rozwiązywaniu zadań dotyczących trójkątów, często mamy do czynienia z różnymi miarami kątów. Istnieje łatwy sposób na konwersję kątów z radianów na stopnie i stopni na radiany:

• Jeśli kąt jest w radianach, żeby otrzymać stopnie, pomnóż go razy 180/π.
• Jeśli kąt jest w stopniach, żeby otrzymać radiany, pomnóż go razy π/180.

Czasami możesz spotkać się z problemem, w którym brakuje dwóch lub nawet trzech długości boków. W takich przypadkach kalkulator trójkąta prostego, kalkulator przeciwprostokątnej, czy wzór na pole trójkąta prostokątnego nie pomogą. Musisz użyć funkcji trygonometrycznych, aby znaleźć brakujące parametry.

Trójkąt prostokątny jest tylko jednym z wielu wyróżniających się trójkątów. Trójkąty mogą mieć jedną lub więcej specjalnych cech, które czynią je wyjątkowymi. Na przykład, jak widzieliśmy, trójkąt prostokątny ma kąt prosty oraz przeciwprostokątną, co czyni go wyjątkowym rodzajem trójkąta. Oprócz trójkąta prostokątnego istnieją inne specjalne trójkąty o interesujących cechach.

Jednym z takich trójkątów jest trójkąt równoboczny, którego charakteryzują trzy równe boki i kąty (wszystkie kąty mają po 60°). To sprawia, że wykonanie kalkulatora trójkąta równobocznego jest bardzo proste, ponieważ nie trzeba znać dużej ilości parametrów.

Innym ze szczególnych trójkątów jest trójkąt równoramienny, który ma 2 boki równej długości, a co za tym idzie dwa kąty o tej samej wielkości. W przeciwieństwie do trójkąta równobocznego trójkąty równoramienne mają bardziej zmienne kształty.

Istnieje jeszcze wiele innych specjalnych trójkątów. Jednak teraz, wróćmy do trójkątów prostokątnych i ich szczególnym przypadków, które oprócz tego, że są trójkątami prostokątnymi, mają inne unikalne właściwości, które czynią je interesującymi.

Tak zwany trójkąt „45 45 90” jest chyba najbardziej wyróżniający się wśród wszystkich specjalnych trójkątów prostokątnych. Jest to trójkąt prostokątny, który dodatkowo jest trójkątem równoramiennym. Obie przyprostokątne takiego trójkąta są tej samej długości, a ponadto ma on tę cechę, że dwa z jego kątów są dokładnie o połowę mniejsze od kąta prostego.

Taki trójkąt można otrzymać, gdy podzielimy kwadrat przez jego przekątną. Wtedy obie przyprostokątne (boki kwadratu) są równej długości. Dla tych, którzy chcą dowiedzieć się więcej o tym najspecjalniejszym ze specjalnych trójkątów prostokątnych, polecamy zajrzeć do kalkulatora trójkąta 45 45 90.

Innym fascynującym trójkątem z grupy specjalnych trójkątów prostych jest tzw. trójkąt „30 60 90”. Jego nazwa pochodzi od tego, że ma jeden kąt prosty (90°), jeden kąt o mierze 30°, oraz ostatni o mierze 60°. Kąty te są szczególne ze względu na wartości ich funkcji trygonometrycznych (cosinus, sinus, tangens itp.). Konsekwencje tego można zobaczyć i zrozumieć za pomocą kalkulatora trójkąta 30 60 90, ale dla tych, którzy są zbyt leniwi, by kliknąć link, przypomnimy niektóre z nich tutaj. Zakładając, że krótszy bok ma długość a:

1. Druga przyprostokątna jest równa a√3;
2. Przeciwprostokątna jest równa 2a;
3. Pole powierzchni jest równe (a²√3)/2; oraz
4. Obwód jest równy a(3 + √3).

Na pierwszy rzut oka może się wydawać, że trójkąt prostokątny i równoległobok nie mają ze sobą nic wspólnego. Jak narzędzie do znajdywania parametrów trójkątów może pomóc w zrozumieniu równoległoboku? W rzeczywistości każdy równoległobok można rozłożyć na 2 lub więcej trójkątów prostych. Na przykład, spójrzmy na prostokąt:

Wyobraź sobie dowolny prostokąt. Narysuj ślad na jednej z przekątnych tego prostokąta. Jeśli rozdzielimy prostokąt przekątną, to otrzymamy dwa trójkąty prostokątne. Patrząc na te trójkąty, nie trzeba używać kalkulatora trójkątów prostokątnych, aby przekonać się, że oba są równe, a ich pola takie same. Oznacza to, że pole prostokąta jest dwukrotnie większe niż pole każdego z tych trójkątów.

Uzyskamy dodatkowe potwierdzenie tej teorii, jeśli zastanowimy się nad równaniami opisującymi te figury. Pole prostokąta o bokach a i b wynosi dokładnie a ∙ b. Natomiast, dla trójkąta prostokątnego, pole wynosi podstawa ∙ wysokość / 2, co w tym przypadku oznaczałoby a ∙ b / 2. To pokazuje nam, że pole wyciętego trójkąta jest dwa razy mniejsze niż pole prostokąta.

To samo możemy zaobserwować dla kwadratów. Dla innych równoległoboków jest to nieco bardziej skomplikowane — równoległobok może obejmować nawet 4 trójkąty proste o różnych rozmiarach. Mimo to, przy odrobinie wprawy, możesz wykorzystać ten sam pomysł i obliczyć pole równoległoboku, używając trójkątów prostokątnych. A jeśli zależy ci na czasie, możesz użyć naszego kalkulatora.

Geometria i wielokąty, a zwłaszcza trójkąty, są nierozłączne. Własności niektórych trójkątów, takich jak trójkąty prostokątne, są często interesujące i szokujące, nie tylko dla matematyków. Przyjrzymy się teraz interesującym zestawom liczb ściśle związanych z trójkątami prostokątnymi, które uwielbiają matematycy.

Te zbiory liczb nazywane są trójkami pitagorejskimi. Są to zbiory 3 liczb całkowitych (nazwijmy je a, b i c) spełniających twierdzenie Pitagorasa: a² + b² = c². To znaczy, że można z nich stworzyć trójkąt prostokątny o bokach o długościach a, b i c. Ilość zestawów liczb, które posiadają tę cechę jest ograniczona, ale matematycy znajdują radość w poszukiwaniu nowych.

Takie zbiory liczb mają pewne interesujące właściwości, wykorzystywane między innymi w kryptografii. Biorąc pod uwagę zastosowania, jakie można znaleźć dla takich zestawów liczb, matematycy wyszli nawet poza trójki, używając czterech, pięciu... czy więcej zestawów liczb, które spełniają podobną relację, w której suma kwadratów wszystkich liczb z wyjątkiem jednej, daje kwadrat liczby, która pozostała.

Z trójkami pitagorejskimi związane jest też niesławne wielkie twierdzenie Fermata, w którym niemal legendarny matematyk kryptolog Pierre Fermat stwierdził, że nie może istnieć zbiór trzech liczb całkowitych, który spełniałby relację: aⁿ + bⁿ = cⁿ dla n większych od 2. To przypuszczenie zostało udowodnione w 1995 roku, ponad 300 lat po sformułowaniu i jest uważane za jeden z najważniejszych problemów matematycznych stulecia.

Już dużo opowiedzieliśmy o trójkątach, zwłaszcza o trójkątach prostokątnych, i ich zastosowaniach w matematyce i geometrii. To, o czym jeszcze nie mówiliśmy, to o użyteczności trójkątów prostokątnych do obliczania zjawisk z codziennego życia. Może się wydawać, że zastosowania poza geometrią będą ograniczone, ale przyjrzyjmy się zjawisku cieni.

Tak, cienie. Ciemny obrys rzucany przez obiekt, gdy jest on oświetlony. Jeśli spojrzysz na kształt utworzony przez cień, obiekt i ziemię, zauważysz, że tworzą one trójkąt prostokątny! Przynajmniej w przypadku, gdy obiekt jest idealnie pionowy, a ziemia pozioma. Wtedy, możemy użyć kalkulatora trójkątów prostokątnych, aby znaleźć różne informacje o obiektach oświetlanych przez słońce. Zobaczmy, jak to zrobić.

Wyobraź sobie, że chcesz poznać wysokość budynku. Nie możesz go zmierzyć bezpośrednio, bo jest zbyt wysoki, by zmierzyć go taśmą mierniczą. To, co możesz zrobić, to zmierzyć długość cienia na ulicy. Następnie, przy pomocy dowolnego narzędzia do pomiaru kątów i kartki papieru, możesz wyznaczyć kąt pomiędzy rzucanym cieniem a ziemią. Wiedząc, że kąt między budynkiem a ziemią wynosi 90°, możesz obliczyć wysokość budynku.

Używając tej techniki, możesz mierzyć wysokość różnych obiektów, o ile jest jasny słoneczny dzień lub inne, stabilne światła oświetlające obiekt. Była to bardzo powszechna technika pomiarowa w dawnych czasach. Prawdopodobnie najciekawszym i najbardziej zdumiewającym zastosowaniem trójkątów prostokątnych jest przypadek Eratostenesa, któremu udało się wykorzystać trójkąty prostokątne i cienie do zmierzenia promienia Ziemi. Jak tego dokonał?

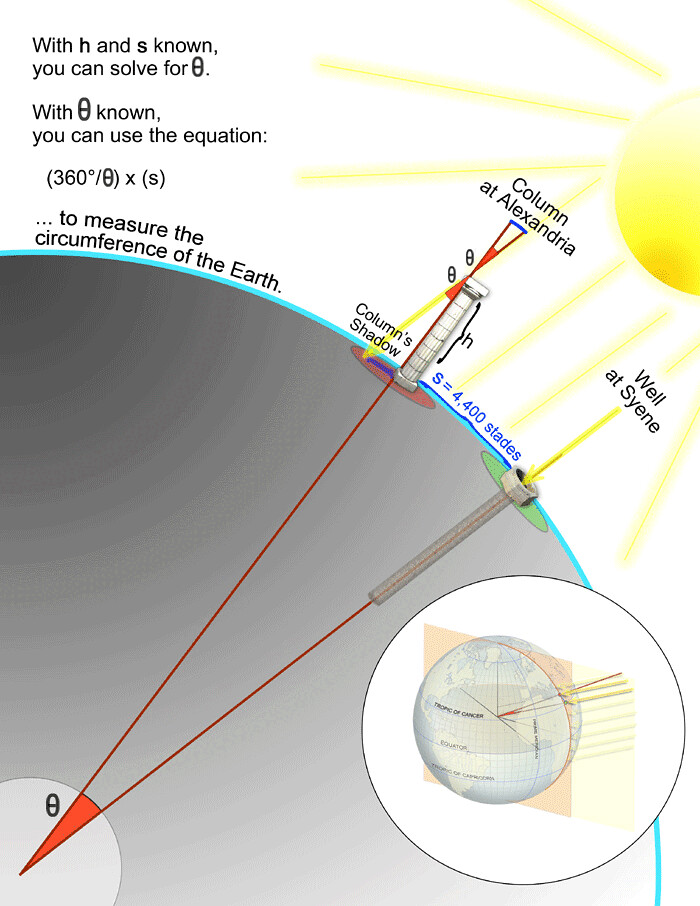
Eratostenes zauważył, że w czasie letniego przesilenia w pewnym miejscu na Ziemi, w studniach nie było w południe cienia, tzn. słońce świeciło na nie prosto w dół. Zauważywszy to, ustawił słup o znanej wysokości w określonej odległości od tej studni i zmierzył wielkość cienia tworzonego przez słup w południe w dzień przesilenia. Następnie używając trójkątów prostokątnych i trygonometrii, był w stanie określić kąt idący od środka Ziemi między studnią a słupem, a także promień Ziemi, na podstawie znanej odległości między tymi punktami.

Dokładność jego pomiaru była dość zdumiewająca, biorąc pod uwagę dosyć niedokładne narzędzia, do których miał dostęp. Teraz można by było powtórzyć jego osiągnięcie o wiele łatwiej, na przykład, korzystając z kalkulatorów Omni, które stworzyliśmy dla ciebie.