Omni Calculator logo
Ostatnia aktualizacja:

Kalkulator pola powierzchni trójkąta prostokątnego

Nowy

Spis treści

Wzory na pole trójkąta prostokątnegoPole trójkąta równoramiennego prostegoJak korzystać z kalkulatora pola trójkąta prostokątnegoFAQs

Jeśli zastanawiasz się jak znaleźć pole trójkąta prostokątnego, to jesteś we właściwym miejscu — ten kalkulator pola trójkąta prostokątnego jest narzędziem dla ciebie.

Niezależnie od tego, czy szukasz równania na boki trójkąta, ramię i przeciwprostokątną, czy bok i kąt, nie zawiedziesz się — ten kalkulator ma je wszystkie.

Przewiń w dół, aby dowiedzieć się więcej o wzorach na pole trójkąta prostokątnego lub po prostu wypróbuj nasz kalkulator!

Wzory na pole trójkąta prostokątnego

🙋 Jeśli właśnie zauważyłeś/aś, że twój trójkąt nie jest trójkątem prostokątnym, sprawdź nasz ogólny kalkulator pola trójkąta.

Trójkąt prostokątny z zaznaczonymi wysokościami

Podstawowe równanie jest przekształconą wersją standardowego wzoru na wysokość trójkąta (a⋅h/2a \cdot h / 2). Ponieważ ramiona trójkąta prostokątnego są do siebie prostopadłe, jedno ramię jest traktowane jako podstawa, a drugie jako wysokość trójkąta prostokątnego:

pole=a⋅b2\text{pole}=\frac{a\cdot b}{2}

Czasami nie jest to takie oczywiste — masz podane inne wartości, a nie dwa ramiona. Co wtedy?

  1. Jeśli masz jedno ramie i przeciwprostokątną, użyj twierdzenia Pitagorasa, aby znaleźć brakujące ramię:
a2+b2=c2\qquad a^2+b^2=c^2

Następnie oblicz pierwiastek kwadratowy 🇺🇸 przekształconego równania:

Biorąc pod uwagę aa i cc stwierdzamy, że b=c2−a2b = \sqrt{c^2 - a^2}:

pole=a⋅c2−a22\qquad\text{pole}=a\cdot\frac{\sqrt{c^2-a^2}}{2}

Biorąc pod uwagę bb i cc obliczamy, że a=c2−b2a = \sqrt{c^2 - b^2}:

pole=b⋅c2−b22\qquad \text{pole} = b\cdot\frac{\sqrt{c^2-b^2}}{2}
  1. Jeśli znasz jeden kąt i przeciwprostokątną, możesz użyć kalkulatora twierdzenia sinusów na takim przykładzie:
a=c⋅sin⁡(α)\qquad a=c\cdot\sin(\alpha)

Stąd:

b=c⋅sin⁡(β)=c⋅sin⁡(90°−α)=c⋅cos⁡(α)\qquad \begin{split} b&=c\cdot\sin(\beta)\\&=c\cdot\sin(90\degree-\alpha)\\ &=c\cdot\cos(\alpha) \end{split}

Tak więc:

pole=c2⋅sin⁡(α)⋅cos⁡(α)2\qquad \text{pole}=c^2\cdot\sin(\alpha)\cdot\frac{\cos(\alpha)}{2}
  1. Biorąc pod uwagę jeden kąt i jedno ramię, znajdź pole używając np. funkcji trygonometrycznych:
ab=tan⁡(α)\qquad\frac{a}{b}=\tan(\alpha)

oraz:

ba=tan⁡(β)\qquad\frac{b}{a}=\tan(\beta)

Stwierdzamy:

pole=b⋅tan⁡(α)⋅b2=b2⋅tan⁡(α)2\qquad \begin{split} \text{pole}&=b\cdot\tan(\alpha)\cdot\frac{b}{2}\\ \\[1.5em] &=b^2\cdot\frac{\tan(\alpha)}{2} \end{split}

Lub:

pole=a⋅a⋅tan⁡(β)2=a2⋅tan⁡(β)2\qquad \begin{split} \text{pole}&=a\cdot a\cdot \frac{\tan(\beta)}{2}\\[1em] &=a^2\cdot\frac{\tan(\beta)}{2} \end{split}

🙋 Chcesz dowiedzieć się więcej o trójkątach prostokątnych? Odwiedź nasz kalkulator trójkątów prostokątnych!

Pole trójkąta równoramiennego prostego

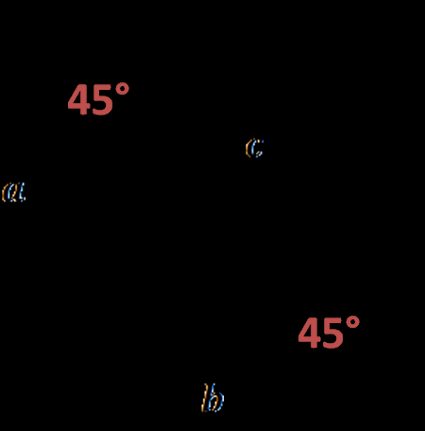
trójkąt równoramienny prosty

Trójkąt równoramienny to specjalnym trójkątem prostokątnym, czasami nazywany trójkątem 45-45-90 (jest tak wyjątkowy, że stworzyliśmy narzędzie tylko dla niego, kalkulator trójkątów 45 45 90). W takim trójkącie prostokątnym ramiona są równej długości (przeciwprostokątna zawsze musi być najdłuższym z boków trójkąta prostokątnego):

a=ba=b

Jedna ramię to podstawa, a druga to wysokość — między nimi jest kąt prosty. Zatem pole trójkąta równoramiennego prostokątnego wynosi:

pole=a22\text{pole}=\frac{a^2}{2}

Jak korzystać z kalkulatora pola trójkąta prostokątnego

Pokażmy obliczenia krok po kroku:

  1. Wybierz jedną opcję, w zależności od tego, co masz podane. Załóżmy, że znamy jedno ramię i kąt, więc zmieniamy wybór na podany kąt i jeden bok.

  2. Wprowadź wartości. Na przykład wiemy, że α=40°\alpha = 40\degree i bb to 17 cali17\ \text{cali}.

  3. Obejrzyj nasz kalkulator pola trójkąta prostokątnego wykonujący wszystkie obliczenia za ciebie! Pole wybranego trójkąta to 121,25 cali2121,25\ \text{cali}^2.

FAQs

Jak znaleźć pole trójkąta prostokątnego o danych bokach?

Metoda zależy od tego, które boki znasz:

  • Jeśli znasz dwa ramiona, użyj wzoru pole = a ⋅ b / 2, gdzie a i b są ramionami.

  • Jeśli znasz jedno ramię a i przeciwprostokątną c, to użyj wzoru: pole = a × √(c² - a²) / 2.

Jakie jest pole trójkąta prostokątnego o przeciwprostokątnej 5 cm i kącie 45°?

Pole wynosi 6,25. Otrzymujemy tę odpowiedź stosując wzór pole = c² ⋅ sin(α) ⋅ cos(α) / 2 z c = 5 i α = 45°. Twierdzenie matematyczne użyte do wyprowadzenia tego wzoru nazywane jest prawem sinusów.

Skąd mam wiedzieć, czy jest to trójkąt prostokątny?

Jeśli masz trzy boki trójkąta i chcesz wiedzieć, czy ten trójkąt jest prostokątny, sprawdź, czy prawdziwe jest twierdzenie Pitagorasa: a² + b² = c², gdzie c to najdłuższy bok, a a i b to dwa pozostałe boki.

Jak nazywamy boki trójkąta prostokątnego?

Dwa boki prostopadłe do siebie nazywane są ramionami. Bok przeciwległy do kąta prostego (innymi słowy, najdłuższy bok) to przeciwprostokątna.

Trójkąt prostokątny o bokach a, b, c.

© Omni Calculator

Check out 19 similar triangle calculators 🔺
30 60 90 triangle45 45 90 triangleCircumscribed circle...16 more