Kalkulator pola bryły

Omni kalkulator pola powierzchni pomoże ci znaleźć pole powierzchni najczęściej spotykanych trójwymiarowych brył. Jeśli kiedykolwiek zastanawiałeś/aś się, jak obliczyć pole powierzchni lub jakie jest pole powierzchni bocznej danej bryły, ten kalkulator jest dla ciebie. Pole powierzchni ma gigantyczną listę zastosowań w każdej dziedzinie, na przykład w aerodynamice

W tym artykule znajdziesz wzory na pole powierzchni kuli, sześcianu, walca, stożka, ostrosłupa i graniastosłupa prostokątnego/trójkątnego. Wyjaśnimy również, jak obliczyć pole powierzchni kuli na przykładzie.

Pole powierzchni jest całkowitą powierzchnią pokrywającą obiekt od zewnątrz. Innymi słowy, jest to całkowite pole powierzchni obiektu 3D.

Czasami powierzchnia może być podzielona na sumę powierzchni podstawy i powierzchni bocznej. Powierzchnia boczna to powierzchnia wszystkich boków obiektu, z wyłączeniem jego podstaw. Podział ten jest stosowany w przypadku kształtów, w których istnieje oczywiste rozróżnienie między podstawą a pozostałymi częściami — np. w przypadku walca, stożka, ostrosłupa lub graniastosłupa trójkątnego. Rzadko stosuje się go do brył, co do których nie jesteśmy pewni, które powierzchnie powinny być traktowane jako podstawy (jak w przypadku sześcianu lub pudełka), a także nie używamy go dla gładkich powierzchni, takich jak kula.

Nasz kalkulator pola powierzchni może obliczyć pole powierzchni siedmiu różnych brył. Wzór zależy od rodzaju bryły geometrycznej.

• Pole powierzchni kuli: P = 4πr², gdzie r oznacza promień kuli.

• Pole powierzchni sześcianu: P = 6a², gdzie a oznacza długość boku.

• Pole powierzchni walca: P = 2πr² + 2πrh, gdzie r to promień, a h to wysokość walca.

• Pole powierzchni stożka: P = πr² + πr√(r² + h²), gdzie r to promień, a h określa wysokość stożka.

• Pole powierzchni graniastosłupa prostokątnego (pudełka): P = 2(ab + bc + ac), gdzie a, b i c są długościami trzech boków prostopadłościanu.

• Pole powierzchni graniastosłupa trójkątnego: P = 0,5 ⋅ √((a + b + c) ⋅ (-a + b + c) ⋅ (a - b + c) ⋅ (a + b - c)) + h ⋅ (a + b + c), gdzie a, b i c to długości trzech boków podstawy graniastosłupa trójkątnego, a h stanowi wysokość (długość) graniastosłupa.

• Pole powierzchni ostrosłupa: P = l ⋅ √(l² + 4 ⋅ h²) + l², gdzie l to długość boku kwadratowej podstawy, a h to wysokość ostrosłupa.

Ale skąd pochodzą te wzory? Jak znaleźć pole powierzchni podstawowych kształtów 3D? Czytaj dalej, aby się dowiedzieć!

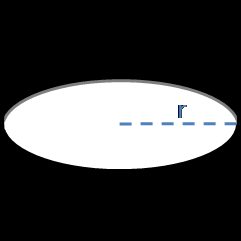
Aby obliczyć pole powierzchni kuli, jedyne co musisz wprowadzić to jej promień lub średnicę.

• P = 4 ⋅ π ⋅ r², gdzie r to promień.

Ponieważ wiemy, że średnica kuli jest równa dwóm promieniom d = 2r, możemy przekształcić równanie do innej postaci:

• P = 4 ⋅ π ⋅ (d / 2)² = π ⋅ d², gdzie d to średnica kuli.

Wyprowadzenie tego wzoru na pole powierzchni wymaga całkowania.

Aby obliczyć pole powierzchni walca, potrzebujesz dwóch wartości: promienia (lub średnicę) podstawy i wysokości walca. Ogólne równanie jest standardowe — pole podstawy (właściwie: pola dwóch podstaw) plus pole powierzchni bocznej. W naszym przypadku podstawą jest okrąg.

• P = 2πr² + 2πrh

Skąd pochodzi ten wzór? Równanie na pole powierzchni walca możesz zapisać jako:

• P = P(bok) + 2 ⋅ P(podstawa)

Łatwo jest znaleźć pole podstawy — pamiętamy dobrze znany wzór na pole koła: P(podstawa) = π ⋅ r². Ale jaki jest kształt pola powierzchni bocznej? Spróbuj sobie wyobrazić, że rozwijamy jego bok na płaskiej powierzchni. Potrafisz sobie wyobrazić powstałą figurę? To prostokąt! Jedna długość boku to wysokość walca, a druga to rozłożony obwód okręgu podstawy.

• P(podstawa) = π ⋅ r²
• P(boczna) = h ⋅ (2 ⋅ π ⋅ r)

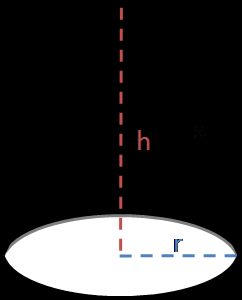
Możemy podzielić powierzchnię stożka na dwie części:

• P = P(bok) + P(podstawa), ponieważ mamy tylko jedną podstawę, w przeciwieństwie do walca.

Podstawa jest ponownie polem koła P(podstawa) = π ⋅ r², ale pochodzenie powierzchni bocznej może nie być tak oczywiste:

• P(bok) = π ⋅ r ⋅ √(r² + h²)

Przyjrzyjmy się temu równaniu krok po kroku:

1. Rozwiń powierzchnię boczną na płasko. Jest to wycinek kołowy, który odpowiada części okręgu o promieniu s (s jest długością tworzącej stożka).

2. Dla okręgu o promieniu s obwód jest równy 2 ⋅ π ⋅ s. Długość obwodu okręgu stanowiącego podstawę naszego stożka jest równa 2 ⋅ π ⋅ r.

3. Pole powierzchni wycinka — który jest naszą boczną powierzchnią — obliczymy wzorem:

• P(bok) = (s ⋅ (długość łuku)) / 2 = (s ⋅ 2 ⋅ π ⋅ r) / 2 = π ⋅ r ⋅ s

  Wzór można uzyskać z proporcji, ponieważ stosunek powierzchni kształtów jest taki sam jak stosunek długości łuku do obwodu:

  (pole wycinka) / (pole dużego okręgu) = (długość łuku) / (obwód dużego okręgu) więc:

  (pole wycinka) / (π ⋅ s²) = (2 ⋅ π ⋅ r) / (2 ⋅ π ⋅ s)

  (powierzchnia wycinka) = (π ⋅ s²) ⋅ (2 ⋅ π ⋅ r) / (2 ⋅ π ⋅ s)

• P(bok) = π ⋅ r ⋅ s

  Aby znaleźć brakujący człon tego stosunku, możesz również wypróbować nasz kalkulator stosunku 🇺🇸!

4. Zazwyczaj nie mamy podanej wartości s, ale h, która jest wysokością stożka, Ale dla nas to żaden problem! Możemy łatwo przekształcić wzór, używając twierdzenia Pitagorasa:

• r² + h²= s², więc biorąc pierwiastek kwadratowy otrzymujemy s = √(r² + h²)

  Zatem wzór na pole powierzchni bocznej wygląda następująco:

• P(bok) = π ⋅ r ⋅ √(r² + h²)

5. Na koniec dodaj pole podstawy i części bocznej, aby znaleźć ostateczny wzór na pole powierzchni stożka:

• P = P(bok) + P(podstawa) = π ⋅ r ⋅ s + π ⋅ r² biorąc pod uwagę r i s lub
• P = π ⋅ r ⋅ √(r² + h²) + π ⋅ r² biorąc pod uwagę r i h.

Pole powierzchni sześcianu 🇺🇸 jest bardzo proste w obliczeniu: każdy z boków jest kwadratem! Ponieważ każdy sześcian ma sześć identycznych kwadratowych ścian, pole powierzchni jest równe:

• P = 6 ⋅ (pole powierzchni jednej ściany)

Ponieważ pole kwadratu jest iloczynem długości jego boków, ostateczny wzór na pole powierzchni sześcianu to:

• P = 6 ⋅ l², gdzie l to bok kwadratu

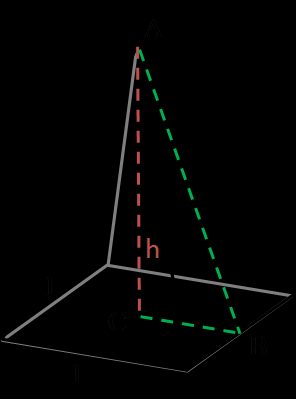
Ostrosłup to bryła 3D o jednej podstawie i trójkątnych ścianach bocznych. Kiedy słyszysz ostrosłup, zwykle zakłada się, że jest to zwykły ostrosłup czworokątny z kwadratem w podstawie. Ale w zależności od kształtu podstawy, może to być również ostrosłup sześciokątny lub prostokątny. Regularny oznacza, że ma regularną podstawę wielokąta i jest ostrosłupem prawidłowym (wierzchołek bezpośrednio nad środkiem podstawy), a kwadratowy — oznacza, że ma ten kształt jako podstawę. Jest to opcja, której użyliśmy jako ostrosłup w naszym kalkulatorze powierzchni.

Wzór na pole powierzchni ostrosłupa to:

• P = l ⋅ √(l² + 4 ⋅ h²) + l², gdzie l to bok podstawy, a h to wysokość ostrosłupa

Ponownie, możemy podzielić równanie na:

P = P(podstawa) + P(bok) = P(podstawa) + 4 ⋅ P(bok)

Podstawa ma kształt kwadratu, więc P(podstawa) = l². Aby obliczyć pole powierzchni bocznej, zacznijmy od pola powierzchni jednej ściany trójkąta:

1. Aby znaleźć wysokość trójkąta, będziemy potrzebować wzoru na przeciwprostokątną więc:

   c = √(a² + b²)

2. Oblicz przeciwprostokątną trójkąta ABC (która jest jednocześnie wysokością ściany trójkąta):

   c = √(h² + (l/2)²) = √(h² + l²/4)

3. Pole trójkąta (w naszym przypadku jest to trójkąt równoramienny) można obliczyć jako:

   P = wysokość ⋅ podstawa / 2 więc

   P(bok) = √(h² + l²/4) ⋅ l / 2

4. Ostateczny wzór na pole powierzchni ostrosłupa to:

   P = l² + 4 ⋅ √(h² + l²/4) ⋅ l / 2 = l² + 2 ⋅ l ⋅ √(h² + l²/4)

   P = l² + l ⋅ √(4 ⋅ h² + l²)

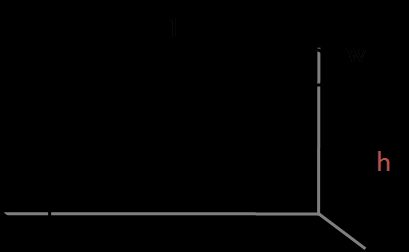
Aby obliczyć pole powierzchni prostopadłościanu, wystarczy obliczyć pola powierzchni jego boków:

• P = 2 ⋅ (P1 + P2 + P3)

gdzie:

• P1 = l ⋅ w
• P2 = w ⋅ h
• P3 = l ⋅ h

Zatem ostateczny wzór to:

• P = 2 ⋅ (l ⋅ w + w ⋅ h + l ⋅ h)

Aby zrozumieć, skąd bierze się wzór na pole powierzchni graniastosłupa trójkątnego, przyjrzyjmy się temu wyprowadzeniu:

1. Boczna część pola powierzchni jest w tym przypadku łatwa do obliczenia. Jak widać na rysunku, graniastosłup składa się z trzech prostokątów o jednej wspólnej długości boku:

   P(bok) = a ⋅ h + b ⋅ h + c ⋅ h = h ⋅ (a + b + c)

   co możemy również zapisać w skrócie jako:

   P(bok) = h ⋅ Obw, gdzie Obw jest obwodem jednego z trójkątów (podstaw)

2. Następnie znajdź pole podstawy trójkąta. Możesz to zrobić na wiele sposobów, w zależności od tego, co masz do dyspozycji. W naszym kalkulatorze zaimplementowaliśmy obliczenia oparte na wzorze Herona 🇺🇸 — jest on używany, gdy masz podane trzy boki trójkąta (SSS).

   P(podstawa) = 0,25 ⋅ √((a + b + c) ⋅ (-a + b + c) ⋅ (a - b + c) ⋅ (a + b - c)))

3. Ostateczny wzór na pole powierzchni graniastosłupa trójkątnego to:

   P = P(bok) + 2 ⋅ P(podstawa)

   A = h ⋅ (a + b + c) + 0,5 ⋅ √((a + b + c) ⋅ (-a + b + c) ⋅ (a - b + c) ⋅ (a + b - c))

Możesz obliczyć powierzchnię dowolnej bryły, na przykład swojego ciała — nie musi to być prosty kształt geometryczny! Jeśli jesteś ciekaw, jaka jest zewnętrzna powierzchnia ludzkiego ciała, sprawdź Omni kalkulator powierzchni ciała.

Jeśli chcesz znaleźć pole powierzchni kuli, musisz wykonać następujące kroki:

1. Określ promień kuli. Możemy przyjąć promień 10 cm.

2. Wprowadź tę wartość do wzoru:

   P = 4πr²

3. Oblicz wynik:

   P = 4π ⋅ 10² = 1256 cm²

4. Możesz również użyć kalkulatora powierzchni online, aby znaleźć promień kuli, jeśli znasz jej powierzchnię.

Jednostkami powierzchni są zawsze kwadratowe jednostki długości. Na przykład, możesz wyrazić ją w cm², in², ft², m², ale także w akrach i hektarach.

Jeśli chcesz znaleźć objętość dowolnej z tych brył, skorzystaj z naszego kalkulatora objętości.

Aby przeliczyć pole powierzchni sześcianu na długość jego boku, wykonaj następujące kroki:

1. Zapisz pole powierzchni sześcianu.
2. Podziel je przez sześć. Otrzymany wynik to powierzchnia jednej ściany.
3. Weź pierwiastek kwadratowy z liczby z kroku 2.
4. Jest to długość każdego boku twojej kostki. Dobra robota!

Wyznacz promień kuli na podstawie pola jej powierzchni:

1. Zapisz pole powierzchni kuli.
2. Podziel je przez 4π ≈ 12,566.
3. Weź pierwiastek kwadratowy: √(Powierzchnia / 4π).
4. To wszystko; właśnie obliczyłeś/aś promień! Możesz zweryfikować swój wynik za pomocą kalkulatora powierzchni brył.

Odpowiedź brzmi: 50,2655 centymetrów kwadratowych. Aby wyprowadzić ten wynik, przypomnij sobie, że wzór na pole powierzchni walca to:

Powierzchnia = 2πr(r + h)

Podstawiając r = h = 2, otrzymujemy Powierzchnia = 16π ≈ 50,2655. Pamiętaj o jednostkach! Ponieważ zarówno r, jak i h są w cm, powierzchnia jest w cm kwadratowych.