Convolution Calculator

With Omni's convolution calculator, you can quickly compute the result of convolving two sequences of data. Not yet familiar with this math operation? Scroll down to learn with us! We'll answer the following questions:

• What is convolution?
• How to calculate convolution?
• What is the role of convolution in probability theory?

We'll also go together through an example of computing the convolution of two data sets.

Convolution is a mathematical operation on two sequences (or, more generally, on two functions) that produces a third sequence (or function). Traditionally, we denote the convolution by the star ∗, and so convolving sequences a and b is denoted as a∗b. The result of this operation is called the convolution as well.

The applications of convolution range from pure math (e.g., probability theory and differential equations) through statistics to down-to-earth applications like acoustics, geophysics, signal processing, and computer vision.

Let's discuss how we define convolution.

Consider the two sequences $\vec{a} = \{a_n\}_{n =0}^\infty$ and $\vec{b} = \{b_n\}_{n=0}^\infty$. The use of $\infty$ here simply means that their lengths can be arbitrarily long. Note that we start counting the sequences' terms at $0$, like programmers do. We define the convolution of $\vec{a}$ and $\vec{b}$ as the sequence $\vec{c} = \{c_n\}_{n =0}^\infty$, where

The convolution formula above may look intimidating at first, but it is actually really simple! Explicitly, for the first few terms, we have:

See the pattern? To get $c_n$ (the $n$-th term of the convolution), we compute the products of terms whose indices sum to $n$. Consider $c_2$ — for this term, we need the products of terms whose indices sum to $2$. These are $a_0b_2$, $a_1b_1$, and $a_2b_0$, because $0+2 = 1+1 = 2+0 = 2$! Clever, isn't it?

As we now know what convolution is and what formula has to be used, let's see how to calculate the convolution of two data sets with the help of our tool.

Using this convolution calculator is really simple:

1. Input the data up to fifteen terms per sequence — additional fields will appear as you go.
2. The calculator will summarize your input at the bottom of the calculator. Make sure there's no typos.
3. The result of the convolution will appear at the same place.

Example

Let's go together through an example. We will compute the convolution of [1, 2, 3] with [4, 5, 6]. Let's first compute by hand, using the convolution formula we've discussed in the previous section:

• c₀ = 1 × 4 = 4
• c₁ = 1 × 5 + 2 × 4 = 13
• c₂ = 1 × 6 + 2 × 5 + 3 × 4 = 28
• c₃ = 2 × 6 + 3 × 5 = 27
• c₄ = 3 × 6 = 18

Entering these values into Omni's convolution calc, we see that our calculations are correct. Great!

The convolution of two sequences that we discussed above is, in fact, a special case of a more general math operation: convolving two functions.

Namely, for two real functions $f$ and $g$, their convolution $f * g$ is another function, whose value at $x$ is defined as

From the point of view of signal processing, $f$ describes the signal and $g$ is a filter applied to this signal. The role of the filter may be, e.g., to sharpen or blur the signal, depending on our needs.

The integral formula for convolving two functions promotes the geometric interpretation of the convolution, which is a bit less conspicuous when one looks at the discrete version alone.

First, note that by using $-t$ under the function $g$, we reflect it across the vertical axis. Then, by introducing the time-offset $x$, we slide $g$ horizontally.

Now, for a fixed value of $x$, we integrate the product of $f(t)$ and $g(x-t)$, that is, we compute the area under the function $f(t)$ but weighted by the function $g(x-t)$, i.e., by $g(-t)$ shifted by $x$. And as the value of $x$ changes (let's say it increases), i.e., as $g(-t)$ slides horizontally (from left to right), different parts of the signal $f(t)$ get emphasized by the weighting.

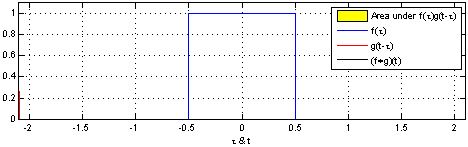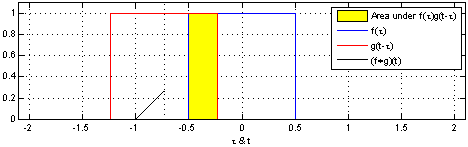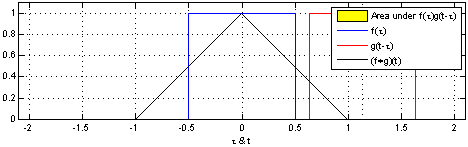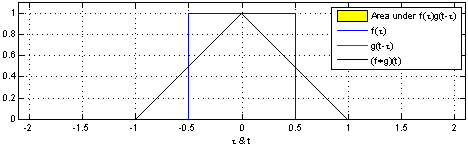
In the picture below, you can see how this procedure works in the particular case of both $f$ and $g$ as the characteristic functions of the interval $[-\frac 12, \frac 12]$, or more visually intuitive, as single periods of square waves. Let us point out that here, the weighting is trivial (constant), so the value of convolution for the argument $x$ is exactly equal to the yellow area at time $x$. Look carefully how the value of the convolution (black line) increases from zero (before the two functions touch) to the maximal value (when they coincide) and then decreases again, hitting zero exactly at the moment of $g$ bidding its final farewell to $f$.

Yes, convolution is commutative, meaning that the order does not matter and that f∗g=g∗f. Moreover, it is associative as well as distributive, i.e. f∗(g∗h)=(f∗g)∗h and f∗(g+h)=(f∗g)+(f∗h).

The unit element of convolution is the sequence with one at the initial position and zeroes elsewhere: {1, 0, 0, 0,...}. We call it a unit sample sequence, discrete-time impulse, or a (discrete) Dirac delta impulse.

To compute the convolution of two sequences (vectors):

1. First multiply the first term of each sequence with one another. This is the first term of the convolution.
2. To get the n-th term of the result:
   • Compute the products a₀b_n, a₁b_n-1, etc., up to a_nb₀. Note that the indices change simultaneously: the first one increases, while the second one decreases.
   • Add together all the terms computed above.
3. Repeat Step 2 for as many terms as you need.
4. Alternatively, use an online convolution calculator.

The well-known theorem in probability says that if we have two independent random variables with probability density functions (PDFs), then the PDF of their sum arises as the convolution of the PDFs of these variables.