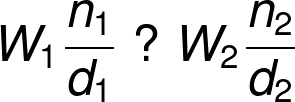Comparing Fractions Calculator

Use this comparing fractions calculator when you are struggling to compare fractions – be they simple fractions, improper fractions, mixed numbers, or even whole numbers. Your fractions don't need to have the same denominator; the tool works perfectly even when comparing fractions with unlike denominators. Like to learn the rules of how to compare fractions? Look no further! 🔍

We'll explain in detail how comparing fractions with the same denominator works, as well as comparing fractions with the same numerator.

There are two popular methods that you can use to compare fractions:

1. Decimal method – where you convert each fraction to a decimal. It's easy when you have a simple pocket calculator or our fraction to decimal converter, so we won't go into details here; and
2. Same denominator method – which we describe thoroughly below, as there's a high chance you're searching for this method 😉

So, in the same denominator method, a few cases may occur:

• Comparing fractions with the same denominator – that's the most straightforward case, of course 😀

• Comparing fractions with the same numerator – also, not a tricky problem 🙂

• Comparing fractions with unlike denominators – may be the most problematic, as you need to find the common denominator or least common denominator. However, it's still a piece of cake, trust us! 🍰

In the paragraphs below, we describe in detail how to compare fractions in each of those cases. Scroll down and find some real-life examples – the battle for each and every pizza slice.

Comparing fractions with the same denominator is the easiest option. If two of your fractions have the same denominator (bottom number), the greater fraction will be the one with a larger numerator (top number). So, for example:

because $4$ is greater than $3$; and

because $3$ is smaller than $6$.

Think of it this way:

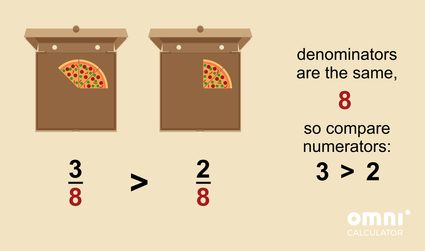
For sure, it's Michael! Three slices 🍕🍕🍕 are definitely more than two slices 🍕🍕, right?

So, what happens if two fractions have the same numerator? Then, the greater fraction is the one with the smaller denominator, e.g.

Coming back to the pizza analogy:

Emily didn't like the idea that Michael took more pizza slices. So, she told everyone that, next time, everybody should take the same number of slices – but her foxy plan was that the slices are not equal in size😈. She cut one pizza to $8$ slices – and gave Michael $3$ slices, and she cut the other pizza to $4$ slices and took $3$ slices for herself. Who has more pizza? The answer is $3/8 <3/4$.

Emily took three bigger slices, so she definitely has more pizza than Michael!

Getting to the heart of the matter – how to compare fractions with unlike denominators, e.g. $3/8$ and $1/6$? There are two methods to make the denominator the same:

1. Common denominator method, where you multiply the top and bottom part of the fraction by the denominator of the other fraction:

2. Least common denominator method (LCD), where you calculate the LCM of the denominators and then the equivalent fractions (for a refresh, visit the equivalent fractions calculator) of both fractions with the LCM as the denominator:

The methods are pretty similar, and you can use whichever you prefer.

Let's go back to our pizza story:

Michael gets a bit offended by Emily's foul game. The next time they met, he asked Emily directly which one she prefers – having $3$ slices out of $8$, or $1$ slice out of $3$? By quick calculations in her head, she has chosen the first option. Was it a good choice?

Thus:

Yes, it was! The difference is not so huge in this case, but the more pizza, the better! 😋

In the above sections, we described cases where you compare simple fractions.
But what happens if you want to compare, e.g., mixed fractions or improper fractions? For sure, you can use our amazing comparing fractions calculator, it can deal with such problems 😎 But do not worry, we'll explain it here too:

1. Comparing with mixed numbers

   When comparing two mixed fractions, sometimes you know immediately which mixed number is bigger – if the whole part is bigger, then the mixed number will be bigger, too:

If the whole number is the same, compare the fraction next to the whole number, as we did in the previous paragraph:

Thus:

2. Comparing with improper fractions

   Comparing two improper fractions works precisely the same as if they were simple fractions!

   If you want to compare mixed fractions to improper fractions – make the fractions of the same type. For this purpose, you can use two of our tools:

   • The improper fraction to mixed number calculator; or
   • The mixed number to improper fraction calculator.

To sum up, the universal solution is:

1. Find a common denominator of your fractions. If one of the fractions is a mixed number, convert it to an improper fraction.

2. Transform the fractions in such a way that they'll have the same common denominator.

3. Compare the top numbers – the fraction with the greater numerator is the greater fraction

We're pretty sure you're a young, intelligent person, and you found out how the comparing fractions calculator works just by playing around with it. But to make things crystal clear 💎, we'll show you how to use our tool step by step.

Let's choose a more complicated case – let's compare fractions with unlike denominators. Additionally, one fraction is a mixed number, and the other is an improper fraction: $1\tfrac{5}{6}$ and $20/11$.

1. Choose the fraction form. As one of our fractions is a mixed number, choose that option.

2. Input the first fraction. For our example, the whole number is $1$, the numerator equals $5$, and the denominator is $6$.

3. Enter the second fraction. We'll leave the 'whole number' box empty, putting $20$ as the numerator and $11$ as the denominator.

4. Tadaa!✨ The comparing fractions calculator shows the result:

What is more, it shows the reasoning behind this result:

• It converts the mixed number to improper fraction: $1\tfrac{5}{6} = 11/6$; and

• Displays the equivalent fractions with the same denominator: $121/66 > 120/66$

Isn't it amazing? 😍