Calcolatore per il Teorema del Coseno

Il calcolatore per il teorema del coseno può aiutarti a risolvere un gran numero di problemi relativi ai triangoli. Scoprirai cos'è il teorema del coseno (noto anche come legge del coseno), la formula del teorema del coseno e le sue applicazioni. Scorri in basso per scoprire quando e come usare il teorema del coseno e scopri le prove di questa legge. Grazie a questo calcolatore per triangoli, potrai trovare rapidamente le proprietà di qualsiasi triangolo.

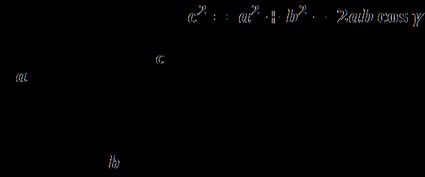
Ma se ti stai chiedendo cosa cavolo sia il coseno, dai un'occhiata al nostro calcolatore del coseno 🇺🇸.

Il teorema del coseno stabilisce che, per un triangolo con lati e angoli indicati con i simboli illustrati sopra,

a² = b² + c² - 2bc × cos(α);

b² = a² + c² - 2ac × cos(β); e

c² = a² + b² - 2ab × cos(γ).

Per un triangolo rettangolo, l'angolo gamma, ovvero l'angolo tra i cateti a e b, è uguale a 90°. Il coseno di 90° = 0, quindi in questo caso speciale la formula del teorema del coseno si riduce alla nota equazione del teorema di Pitagora:

a² = b² + c² - 2bc × cos(90°)

a² = b² + c².

Il teorema del coseno (alternativamente legge del coseno o regola del coseno) descrive la relazione tra le lunghezze dei lati di un triangolo e il coseno dei suoi angoli. Può essere applicata a tutti i triangoli, non solo a quelli rettangoli. Questa legge generalizza il teorema di Pitagora, in quanto permette di calcolare la lunghezza di uno dei lati, dato che si conosce la lunghezza degli altri due lati e l'angolo tra di essi.

La legge apparve ne Gli Elementi di Euclide, un trattato di matematica contenente definizioni, postulati e teoremi di geometria. Euclide non la formulò nel modo in cui la impariamo oggi, poiché il concetto di coseno non era ancora stato sviluppato.

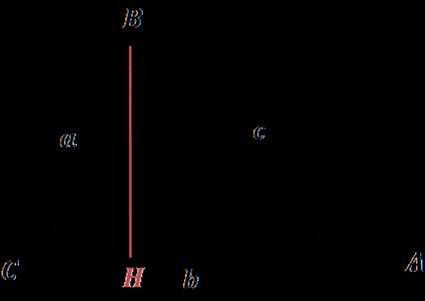
AB² = CA² + CB² - 2 × CA × CH (per gli angoli acuti), e

AB² = CA² + CB² + 2 × CA × CH (per gli angoli ottusi)

Tuttavia, possiamo riformulare facilmente il teorema di Euclide nella forma attuale della formula del coseno:

CH = CB × cos(γ), quindi AB² = CA² + CB² - 2 × CA × (CB × cos(γ))

Cambiando notazione, otteniamo la nota espressione:

c² = a² + b² - 2ab × cos(γ)

La prima equazione esplicita della regola del coseno fu presentata dal matematico persiano d'Al-Kashi nel XV secolo. Nel XVI secolo, il teorema fu reso popolare dal famoso matematico francese Viète prima di ricevere la sua forma definitiva nel XIX secolo.

Puoi trasformare queste formule della legge del coseno per risolvere alcuni problemi relativi ai triangoli. Puoi usarle per trovare:

1. Il terzo lato di un triangolo, conoscendo due lati e l'angolo tra di essi:

   • a = √[b² + c² - 2bc × cos(α)],

   • b = √[a² + c² - 2ac × cos(β)], e

   • c = √[a² + b² - 2ab × cos(γ)];

2. Gli angoli di un triangolo, conoscendo tutti e tre i lati:

   • α = arccos [(b² + c² - a²)/(2bc)],

   • β = arccos [(a² + c² - b²)/(2ac)], e

   • γ = arccos [(a² + b² - c²)/(2ab)];

3. Il terzo lato di un triangolo, conoscendo due lati e l'angolo opposto a uno di essi:

   • a = b × cos(γ) ± √[c² - b² × sin²(γ)],

   • b = c × cos(α) ± √[a² - c² × sin²(α)], e

   • c = a × cos(β) ± √[b² - a² × sin²(β)].

Ricorda che conoscendo due lati e un angolo adiacente puoi ottenere due possibili triangoli distinti (o una o zero soluzioni positive, a seconda dei dati forniti). Ecco perché abbiamo deciso di implementare il calcolo dei due lati e l'angolo tra di essi e dei tre lati in questo strumento, ma non dei due lati e l'angolo opposto a uno di essi.

La legge dei coseni è una delle leggi fondamentali ed è ampiamente utilizzata per molti problemi geometrici. Sfruttiamo questa legge anche in molti strumenti di Omni, per citarne solo alcuni:

• Calcolatore per l'angolo del triangolo;
• Calcolatore per l'area del triangolo;
• Calcolatore per il perimetro del triangolo 🇺🇸;
• Calcolatore per il prisma a base triangolare.

Inoltre, puoi combinare il calcolatore per il teorema del coseno con la legge dei seni per risolvere altri problemi, ad esempio trovare il lato del triangolo dati due angoli e un lato.

Ci sono molti modi per dimostrare la legge del coseno. Ne hai già letto uno: deriva direttamente dalla formulazione della legge di Euclide e da un'applicazione del teorema di Pitagora. Puoi scrivere le altre prove della legge del coseno utilizzando:

1. Trigonometria

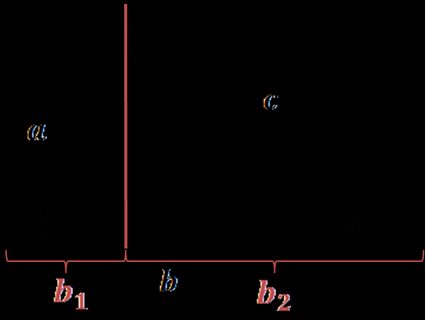
Traccia una linea per l'altezza del triangolo e dividi il lato perpendicolare ad essa in due parti:

b = b₁ + b₂

Dalle definizioni di seno e coseno, b₁ può essere espresso come a × cos(γ) e b₂ = c × cos(α). Quindi:

b = a × cos(γ) + c × cos(α) e moltiplicando per b otteniamo:

b² = ab × cos(γ) + bc × cos(α) (1)

Si possono ricavare equazioni analoghe per gli altri due lati:

a² = ac × cos(β) + ab × cos(γ) (2)

c² = bc × cos(α) + ac × cos(β) (3)

Per concludere la prova della legge dei coseni, devi sommare le equazioni (1) e (2) e sottrarre (3):

a² + b² - c² = ac × cos(β) + ab × cos(γ) + bc × cos(α) + ab × cos(γ) - bc × cos(α) - ac × cos(β)

La riduzione e la semplificazione dell'equazione forniscono una delle forme della regola del coseno:

a² + b² - c² = 2ab × cos(γ)

c² = a² + b² - 2ab × cos(γ)

Cambiando l'ordine in cui vengono sommati e sottratti, puoi ricavare le altre formule della legge del coseno.

2. Formula della distanza

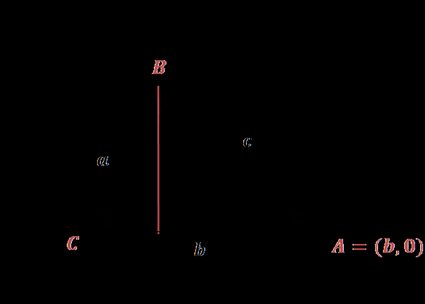
Sia C = (0,0), A = (b,0), come nell'immagine.

Per trovare le coordinate di B, possiamo utilizzare la definizione di seno e coseno:

B = (a × cos(γ), a × sin(γ))

Dalla formula della distanza, possiamo trovare che:

c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a × cos(γ) - b)² + (a × sin(γ) - 0)²]

Quindi:

c² = a² × cos(γ)² - 2ab × cos(γ) + b² + a² × sin(γ)²

c² = b² + a²(sin(γ)² + cos(γ)²) - 2ab × cos(γ)

Poiché la somma dei quadrati di seno e coseno è uguale a 1, otteniamo la formula finale:

c² = a² + b² - 2ab × cos(γ)

3. Teorema di Tolomeo

Un'altra prova della legge dei coseni relativamente facile da capire utilizza il teorema di Tolomeo:

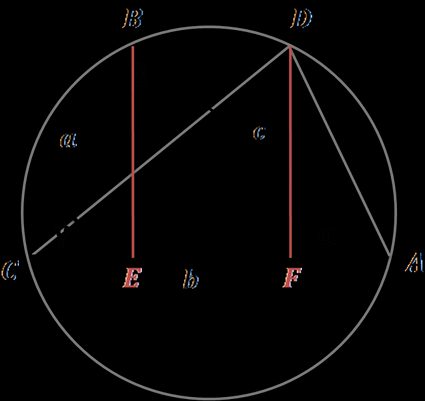
• Supponiamo di avere il triangolo ABC disegnato nella sua circonferenza, come nell'immagine;

• Disegna il triangolo congruente ADC, dove AD = BC e DC = BA;

• Le altezze dei punti B e D dividono la base AC rispettivamente nei punti E ed F. CE è uguale a FA;

• Dalla definizione di coseno, possiamo esprimere CE come a × cos(γ);

• Quindi, possiamo scrivere che BD = EF = AC - 2 × CE = b - 2 × a × cos(γ); e

• Quindi, per il nostro quadrilatero ADBC, possiamo utilizzare il teorema di Tolomeo, che spiega la relazione tra i quattro lati e le due diagonali. Il teorema afferma che per i quadrilateri ciclici, la somma dei prodotti dei lati opposti è uguale al prodotto delle due diagonali:

  BC × DA + CA × BD = AB × CD

  quindi nel nostro caso:

  a² + b × (b - 2 × a × cos(γ)) + a² = c²

• Dopo la riduzione, otteniamo la formula finale:

  c² = a² + b² - 2ab × cos(γ)

Il grande vantaggio di queste tre prove è la loro universalità: funzionano per triangoli acuti, retti e ottusi.

4. Utilizzando la legge dei seni;
5. Utilizzando la definizione di prodotto scalare 🇺🇸;
6. Confronto di aree; e
7. Geometria del cerchio.

Le ultime due prove richiedono la distinzione tra diversi casi di triangoli. Quella basata sulla definizione di prodotto scalare è riportata in un altro articolo, mentre la prova che utilizza la legge dei seni è piuttosto complicata, quindi abbiamo deciso di non riprodurla qui. Se conoscere le prove della legge del coseno ti incuriosisce, dai un'occhiata alla spiegazione di Wikipedia.

1. Inizia formulando il problema: per esempio, puoi conoscere due lati del triangolo e l'angolo che li separa e stai cercando il lato rimanente;

2. Inserisci i valori noti nei campi appropriati di questo calcolatore per triangoli. Ricorda di ricontrollare con il risultato precedente se hai indicato i lati e gli angoli con i simboli corretti; e

3. Guarda il nostro calcolatore per il teorema del coseno che esegue tutti i calcoli per te!

Se il tuo compito è quello di trovare gli angoli di un triangolo dati tutti e tre i lati, non devi fare altro che utilizzare le formule della regola del coseno trasformato:

α = arccos [(b² + c² - a²)/(2bc)];
β = arccos [(a² + c² - b²)/(2ac)]; e
γ = arccos [(a² + b² - c²)/(2ab)].

Calcoliamo uno degli angoli. Supponiamo che a = 4 cm, b = 5 cm e c = 6 cm. Utilizzeremo la prima equazione per trovare α:

α = arccos [(b² + c² - a²)/(2bc)]

= arccos [(5² + 6² - 4²)/(2 × 5 × 6)]

= arccos [(25 + 36 - 16)/60]

= arccos [(45/60)] = arccos [0,75]

α = 41,41°

Puoi calcolare il secondo angolo dalla seconda equazione in modo analogico, mentre il terzo angolo lo puoi trovare sapendo che la somma degli angoli di un triangolo è uguale a 180° (π).

Se vuoi risparmiare tempo, digita le lunghezze dei lati nel nostro calcolatore per il teorema del coseno: il nostro strumento è una scommessa sicura! Segui questi semplici passaggi:

1. Scegli l'opzione in base ai valori indicati. Dobbiamo scegliere la seconda opzione — 3 lati.

2. Inserisci i valori noti: digita i lati: a = 4 cm, b = 5 cm e c = 6 cm.

3. Il calcolatore visualizza il risultato! Nel nostro caso gli angoli sono pari a α = 41,41°, β = 55,77° e γ = 82,82°.

Dopo questa spiegazione, siamo sicuri che hai capito cos'è la legge del coseno e quando usarla. Prova questo strumento, risolvi alcuni esercizi e ricorda che la pratica rende permanenti!