Calcolatore per la Distanza

Hai mai voluto calcolare la distanza da un punto a un altro o la distanza tra città? Ti sei mai chiesto qual è la definizione di distanza? Abbiamo tutte queste risposte e molto altro ancora, compresa una spiegazione dettagliata di come calcolare la distanza tra due oggetti qualsiasi nello spazio 2D. Come bonus, abbiamo un affascinante argomento su come percepiamo le distanze (come, ad esempio, la differenza percentuale); siamo sicuri che ti piacerà!

Preferisci guardare piuttosto che leggere? Impara tutto quello che ti serve in 90 secondi con questo video che abbiamo creato per te:

Prima di parlare di come calcolare la distanza, dovremmo chiarire cos'è una distanza. Il significato più comune è lo spazio monodimensionale tra due punti. Questa definizione è un modo per dire ciò che quasi tutti noi pensiamo della distanza in modo intuitivo, ma non è l'unico modo. Nelle sezioni seguenti vedrai come il concetto di distanza può essere esteso oltre la lunghezza, in più sensi, segnando la svolta alla base della teoria della relatività di Einstein.

Se ci atteniamo alla definizione geometrica di distanza, dobbiamo ancora definire in che tipo di spazio stiamo lavorando. Nella maggior parte dei casi, probabilmente si parla di tre dimensioni o meno, poiché è tutto ciò che possiamo immaginare senza far esplodere il nostro cervello. Per questo calcolatore, ci concentreremo solo sulla distanza 2D (con quella monodimensionale inclusa come caso speciale). Se stai cercando la distanza 3D tra 2 punti, ti invitiamo a utilizzare il nostro calcolatore per la distanza 3D 🇺🇸 creato appositamente per questo scopo.

Per trovare la distanza tra due punti, la prima cosa di cui hai bisogno sono due punti, ovviamente. Questi punti sono descritti dalle loro coordinate nello spazio. Per ogni punto nello spazio 2D, abbiamo bisogno di due coordinate uniche per quel punto. Se vuoi trovare la distanza tra due punti in uno spazio monodimensionale, puoi comunque utilizzare questo calcolatore semplicemente impostando una delle coordinate come la stessa per entrambi i punti. Poiché questo è un caso molto particolare, d'ora in poi parleremo solo di distanza in due dimensioni.

Il passo successivo, se vuoi essere matematicamente, accurato e preciso, è definire il tipo di spazio in cui stai lavorando. No, aspetta, non scappare! È più facile di quanto pensi. Se non sai in quale spazio stai lavorando o se non sei a conoscenza che esista più di un tipo di spazio, molto probabilmente stai lavorando nello spazio euclideo. Questo è infatti lo spazio "predefinito" in cui svolgiamo quasi tutte le operazioni geometriche ed è quello che abbiamo impostato per il calcolatore per operare. Vediamo di approfondire un po' lo spazio euclideo — cos'è, quali proprietà ha e perché è così importante?

Lo spazio euclideo o geometria euclidea è ciò che di solito pensiamo sia 2D prima di ricevere una formazione matematica approfondita su questi aspetti. Nello spazio euclideo, la somma degli angoli di un triangolo è uguale a 180º e i quadrati hanno tutti gli angoli uguali a 90º; sempre. Questo è un dato che diamo tutti per scontato, ma non è vero in tutti gli spazi. Inoltre, non confondiamo lo spazio euclideo con gli spazi multidimensionali. Lo spazio euclideo può avere tutte le dimensioni che vuoi, purché siano in numero finito, e rispettino comunque le regole euclidee.

Non vogliamo annoiarti con definizioni matematiche di cosa sia uno spazio e di cosa renda unico lo spazio euclideo, perché sarebbe troppo complicato da spiegare in un semplice calcolatore per la distanza. Tuttavia, possiamo provare a fornirti alcuni esempi di altri spazi comunemente utilizzati che potrebbero aiutarti a capire perché lo spazio euclideo non è l'unico spazio. Inoltre, speriamo che tu capisca perché non ci preoccuperemo di calcolare le distanze in altri spazi.

Il primo esempio che ti presentiamo è un po' oscuro, ma speriamo che tu possa scusarci, visto che siamo fisici, per aver iniziato con un tipo di spazio molto importante — Lo spazio di Minkowski. Il motivo per cui abbiamo scelto questo tipo di spazio è che è molto comune in fisica, in particolare viene utilizzato nella teoria della relatività, nella relatività generale e anche nella teoria quantistica relativistica dei campi. Questo spazio è molto simile allo spazio euclideo, ma si differenzia da esso per una caratteristica fondamentale; l'aggiunta del prodotto di punti, chiamato anche prodotto interno (da non confondere con il prodotto incrociato).

Sia lo spazio euclideo sia quello di Minkowski sono ciò che i matematici chiamano spazio piano. Ciò significa che lo spazio stesso ha proprietà piane; ad esempio, la distanza più breve tra due punti qualsiasi è sempre una linea retta tra di essi (controlla il calcolatore per l'interpolazione lineare 🇺🇸). Esistono però altri tipi di spazi matematici chiamati spazi curvi in cui lo spazio è intrinsecamente curvo e la distanza più breve tra due punti non è una linea retta.

Questo spazio curvo è difficile da immaginare in 3D, ma per il 2D possiamo immaginare che invece di avere un'area piana, abbiamo uno spazio 2D, ad esempio, curvato a forma di superficie di una sfera. In questo caso, accadono cose molto strane. La distanza più breve da un punto all'altro non è una linea retta, perché qualsiasi linea in questo spazio è curva a causa della curvatura intrinseca dello spazio. Un'altra caratteristica molto strana di questo spazio è che alcune rette parallele 🇺🇸 si incontrano effettivamente in un punto. Puoi provare a capirlo pensando alle cosiddette linee di longitudine che dividono la Terra in molti fusi orari e si incrociano ai poli.

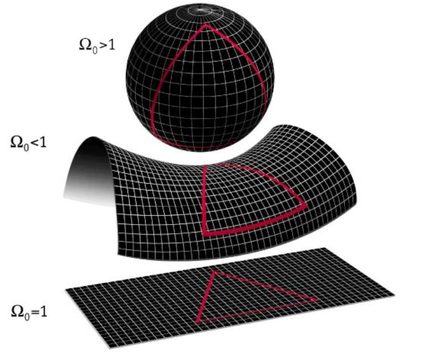
È importante notare che questo è concettualmente MOLTO diverso da un cambio di coordinate. Quando prendiamo le coordinate standard $x, y, z$ e le convertiamo in coordinate polari, cilindriche o addirittura sferiche, ci troviamo ancora nello spazio euclideo. Quando parliamo di spazio curvo, stiamo parlando di uno spazio molto diverso in termini di proprietà intrinseche. In coordinate sferiche, è ancora possibile avere una linea retta e la distanza è ancora misurata in linea retta, anche se sarebbe molto difficile da esprimere in numeri.

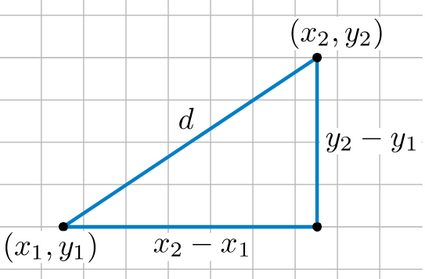
Tornando allo spazio euclideo, possiamo ora presentarti la formula della distanza che ti abbiamo promesso all'inizio. La formula della distanza è

che si riferisce al Teorema di Pitagora, il quale afferma che $a^2+b^2=c^2$. In questo caso, $a$ e $b$ sono i cateti di un triangolo rettangolo e $c$ è l'ipotenusa. Supponiamo che due punti, $(x_1, y_1)$ e $(x_2, y_2)$, siano coordinate agli estremi dell'ipotenusa. Allora $(x_2 - x_1)^2$ nell'equazione della distanza corrisponde a $a^2$ e $(y_2 - y_1)^2$ corrisponde a $b^2$. Dato che $c = \sqrt{a^2 + b^2}$, puoi capire perché si tratta di un'estensione del teorema di Pitagora.

La formula della distanza che abbiamo appena visto è la formula standard della distanza euclidea, ma se ci pensi, può sembrare un po' limitata. Spesso non vogliamo trovare solo la distanza tra due punti. A volte vogliamo calcolare la distanza di un punto da una linea o da un cerchio. In questi casi, dobbiamo prima definire quale punto della linea o della circonferenza utilizzeremo per il calcolo della distanza e poi utilizzare la formula della distanza che abbiamo visto poco sopra.

È qui che il concetto di linea perpendicolare 🇺🇸 diventa fondamentale. La distanza tra un punto e un oggetto continuo è definita dalla perpendicolarità. Da un punto di vista geometrico, il primo passo per misurare la distanza tra un punto e un altro è quello di creare una linea retta tra i due punti e poi misurare la lunghezza di quel segmento. Quando misuriamo la distanza tra un punto e una retta, la domanda diventa "Quale delle tante rette possibili devo tracciare?". In questo caso la risposta è; la linea dal punto che è perpendicolare alla prima linea. Questa distanza sarà pari a zero nel caso in cui il punto sia una parte della retta. Per questi casi monodimensionali, possiamo considerare solo la distanza tra i punti, poiché la linea rappresenta l'intero spazio monodimensionale.

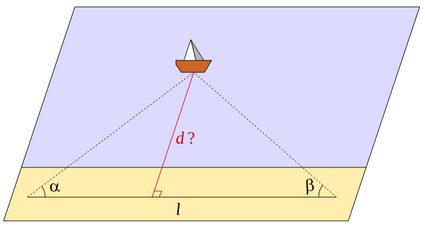
Questo impone restrizioni su come calcolare le distanze in alcune istanze geometriche interessanti. Ad esempio, potremmo ridefinire il concetto di altezza di un triangolo in modo che sia semplicemente la distanza tra un vertice e il lato opposto del triangolo. In questo caso, anche l'area del triangolo viene ridefinita in termini di distanza, poiché l'area è una funzione dell'altezza del triangolo.

Vediamo un paio di esempi nello spazio 2D. Per calcolare la distanza tra un punto e una retta, potremmo procedere passo dopo passo (calcolare il segmento perpendicolare alla retta che va dalla retta al punto e calcolarne la lunghezza) oppure potremmo semplicemente utilizzare questa equazione a portata di mano:

dove la linea è data da $Ax+By+C = 0$ e il punto è definito da $(x_1, y_1)$.

L'unico problema è che una linea retta è generalmente data da $y=mx+b$, quindi dovremmo convertire questa equazione nella forma mostrata in precedenza:

quindi possiamo vedere che $A=m$, $B=-1$ e $C=b$. L'equazione precedente presenta quindi i seguenti valori:

Per la distanza tra due rette, dobbiamo solo calcolare la lunghezza del segmento che va da una all'altra ed è perpendicolare ad entrambe. Anche in questo caso, c'è una semplice formula che ci aiuta:

se le rette sono $A_1x+B_1y+C_1=0$ e $A_2x+B_2y+C_2=0$. Possiamo anche convertire in forma di pendenza-intercetta e ottenere:

per le linee $y=m_1x+b_1$ e $y=m_2x+b_2$.

Da notare che entrambe le rette devono essere parallele, altrimenti si toccherebbero in qualche punto e la loro distanza sarebbe $d=0$. Questo è il motivo per cui le formule omettono la maggior parte dei pedici in quanto per le rette parallele: $A_1=A_2=A$ e $B_1=B_2=B$ mentre nella forma dell'intercetta della pendenza le rette parallele sono quelle per le quali $m_1=m_2=m$.

Come abbiamo già detto, la distanza può avere molti significati, ecco perché in questo calcolatore ti abbiamo fornito diverse opzioni. Puoi calcolare la distanza tra un punto e una linea retta, la distanza tra due linee rette (che devono sempre essere parallele) o la distanza tra punti nello spazio. Quando si tratta di calcolare le distanze tra due punti, hai la possibilità di farlo in 1, 2, 3 o 4 dimensioni. Lo sappiamo, lo sappiamo, 4 dimensioni fanno paura, ma non è necessario utilizzare questa opzione. E puoi sempre saperne di più leggendo alcune belle risorse e sperimentando con il calcolatore. Ti promettiamo che non distruggerà l'Internet o l'universo.

Abbiamo anche aggiunto la possibilità di definire 3 punti diversi nello spazio, dai quali si otterranno le 3 coppie di distanze tra di essi, quindi, se hai più di due punti, questo ti farà risparmiare tempo. Il numero di dimensioni in cui lavori determinerà il numero di coordinate che descrivono un punto; per questo motivo, man mano che aumenti il numero di dimensioni, il calcolatore ti chiederà di inserire più valori.

Anche se l'utilizzo del calcolatore è molto semplice, abbiamo deciso di includere una soluzione passo-passo. In questo modo potrai imparare a conoscere la formula della distanza e a usarla (come se fossimo negli anni '50 e Internet non esistesse ancora). Ora diamo un'occhiata a un esempio pratico — come trovare la distanza tra due punti in 2D.

Supponiamo di avere due coordinate, $(3, 5)$ e $(9, 15)$, e di voler calcolare la distanza tra di esse. Per calcolare la distanza 2D tra questi due punti, segui i seguenti passaggi:

1. Inserisci i valori nella formula: $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$;
2. Nella formula, sottrai i valori tra le parentesi;
3. Eleva al quadrato entrambe le quantità tra le parentesi;
4. Aggiungi i risultati;
5. Prendi la radice quadrata; e
6. Usa il calcolatore per verificare i risultati.

Svolgendo l'esempio a mano, si ottiene:

che è pari a circa $11,\!66$. Tieni presente che quando si svolge la radice quadrata, si otterrà un risultato positivo e uno negativo, ma dato che si tratta di distanza, ti interessa solo il risultato positivo. Il calcolatore svolgerà i calcoli passo dopo passo per darti il risultato in formato esatto e in quello approssimativo.

Vediamo una delle applicazioni del calcolatore per la distanza. Supponiamo che tu stia viaggiando tra le città A e B e che l'unica fermata sia nella città C, con un percorso da A a B perpendicolare al percorso da B a C. Possiamo determinare la distanza da A a B e poi, conoscendo il prezzo del gas, determinare il costo del carburante, il carburante utilizzato e il costo per persona durante il viaggio. Il calcolatore per il gas, che puoi trovare sul nostro sito, può facilitarti questo compito.

La difficoltà sta nel calcolare con precisione le distanze tra le città. Una linea retta (come quella che utilizziamo in questo calcolatore) può essere una buona approssimazione, ma può essere piuttosto sbagliata se il percorso che stai facendo non è diretto ma prevede qualche deviazione, magari per evitare le montagne o per passare da un'altra città. In questo caso, usa Google Maps o qualsiasi altro strumento che calcoli la distanza lungo un percorso e non solo la distanza da un punto all'altro in linea d'aria.

Il nostro calcolatore può fornire misurazioni e previsioni corrette per le distanze tra gli oggetti, non per la lunghezza di un percorso. Tenendo presente questo, ci sono ancora molti scenari in cui potresti essere interessato alla distanza tra gli oggetti, indipendentemente dal percorso che dovresti fare. Uno di questi esempi è la distanza tra oggetti astronomici.

Quando consideriamo una distanza all'interno della nostra Terra, è difficile andare lontano senza imbattersi in alcuni problemi, dalla curvatura intrinseca di questo spazio (dovuta al fatto che la curvatura della Terra non è nulla) alla distanza massima limitata tra due punti della Terra. Per questo motivo, e anche perché c'è un intero universo oltre la nostra Terra, le distanze nell'universo sono di grande interesse per molte persone. Dato che non disponiamo di mezzi adeguati per i viaggi interplanetari, per non parlare di quelli interstellari, concentriamoci per ora sulla distanza euclidea effettiva di alcuni oggetti celesti. Ad esempio, la distanza tra la Terra e il Sole o la distanza tra la Terra e la Luna.

Queste distanze sono al di là dell'immaginabile per i nostri cervelli di scimmia. Facciamo fatica a comprendere le dimensioni del nostro pianeta, per non parlare del vasto e infinito universo. È così difficile che dobbiamo usare la notazione scientifica o gli anni luce come unità di distanza per queste lunghezze. I viaggi più lunghi che si possono fare sulla Terra sono appena un paio di migliaia di chilometri, mentre la distanza tra la Terra e la Luna, il corpo astronomico più vicino a noi, è di 384 000 km. Inoltre, la distanza dalla nostra stella più vicina, ovvero la distanza dalla Terra al Sole, è di 150 000 000 km o poco più di 8 minuti luce.

Se si confrontano queste distanze con la distanza della nostra seconda stella più vicina (Alpha Centauri), che è di 4 anni luce, improvvisamente iniziano a sembrare molto più piccole. Se vogliamo fare un paragone ancora più ridicolo, possiamo sempre pensare a un volo da New York a Sydney, che in genere impiega più di 20 ore e si trova a soli 16 000 km, e confrontarlo con le dimensioni dell'universo osservabile, che è di circa 46 600 000 000 anni luce!

In questo caso, abbiamo inavvertitamente scoperto un'osservazione affascinante, ovvero che non misuriamo le distanze in lunghezza ma in tempo. In questo modo, estendiamo la nozione di distanza oltre il suo senso geometrico. Esploreremo questa possibilità nella prossima sezione quando parleremo dell'importanza e dell'utilità della distanza al di là del senso puramente geometrico. Si tratta di una via molto interessante da seguire ed è ispirata principalmente dalla necessità filosofica di estendere ogni concetto in modo che abbia un significato universale, oltre che dall'ovvia teoria fisica da citare, quando si parla di permutazioni dello spazio e del tempo, o di qualsiasi altra variabile che possa essere misurata.

In genere, il concetto di distanza si riferisce alla distanza geometrica euclidea ed è legato alla lunghezza. Tuttavia, è possibile estendere la definizione di distanza per indicare semplicemente la differenza tra due cose, e allora si apre un mondo di possibilità. Improvvisamente si può decidere qual è il modo migliore per misurare la distanza tra due cose e metterla in termini di quantità più utile. Un passo molto semplice da fare è pensare alla distanza tra due numeri, che non è altro che la differenza monodimensionale tra questi numeri. Per ottenerla, basta sottrarre uno dall'altro e il risultato sarà la differenza, ovvero la distanza.

Potremmo passare da questa distanza numerica a, ad esempio, la differenza o la distanza in termini di differenza percentuale, che in alcuni casi potrebbe fornire un metodo di confronto migliore. Questo è ancora solo un livello di astrazione in cui eliminiamo semplicemente le unità di misura. Ma cosa succederebbe se utilizzassimo unità di misura completamente diverse?

Estendendo il concetto di distanza a qualcosa di più vicino alla differenza, possiamo calcolare la differenza tra due temperature o altre grandezze correlate come la pressione. Ma non c'è bisogno di estremizzare, vediamo come due punti possono essere separati da una distanza diversa, a seconda delle ipotesi fatte. Tornando all'esempio della distanza in auto, potremmo misurare la distanza del viaggio in tempo, invece che in lunghezza. In questo caso, abbiamo bisogno di un'ipotesi per consentire questa traduzione; il mezzo di trasporto.

C'è una grande differenza tra il tempo impiegato per percorrere 10 km in aereo e il tempo impiegato in auto. A volte, però, l'ipotesi è chiara e implicitamente condivisa, come quando misuriamo la distanza in tempo che poi convertiamo in lunghezza. Questo porta a un punto interessante — il fattore di conversione tra distanze temporali e lunghezze è quello che chiamiamo "velocità media" o "velocità" (ricordiamo che non sono esattamente la stessa cosa). A dire il vero, questa velocità media non deve essere costante, come dimostrano i moti accelerati come quello di una caduta libera sotto la forza gravitazionale o quello che collega il tempo di arresto e la distanza di arresto attraverso la forza di rottura e la resistenza o, in casi molto estremi, attraverso la forza di un incidente stradale.

Un'altra istanza in cui si possono trovare strane unità di distanza è la fisica dello stato solido, dove la distanza percorsa da una particella all'interno di un materiale è spesso espressa come una media di interazioni o collisioni. Questa distanza è legata alla lunghezza utilizzando il percorso libero medio, che è la distanza media (in lunghezza) percorsa da una particella tra le interazioni. Se vogliamo essere ancora più stravaganti, possiamo pensare alla distanza tra il valore attuale e il valore futuro di qualcosa come un'automobile.

Non vogliamo però far esplodere il cervello di nessuno, quindi per favore non pensarci troppo. Prendi questo calcolatore e usalo per la distanza basata sulla lunghezza nello spazio 2D. Puoi sempre tornare a questa visione filosofica delle distanze se ti annoi!

Per trovare la distanza tra due punti utilizzeremo la formula della distanza; √[(x₂ - x₁)² + (y₂ - y₁)²]:

1. Ottieni le coordinate di entrambi i punti nello spazio;
2. Sottrai le coordinate x di un punto dall'altro, lo stesso vale per le componenti y;
3. Eleva al quadrato i due risultati separatamente;
4. Somma i valori ottenuti nel passaggio precedente; e
5. Trova la radice quadrata del risultato precedente.

Se pensi che questo sia uno sforzo eccessivo, puoi semplicemente utilizzare il calcolatore per la distanza di Omni.

La distanza non è un vettore. La distanza tra punti è una quantità scalare, cioè è definita solo dal suo valore. Tuttavia, lo spostamento è un vettore con verso e direzione. Quindi la distanza tra A e B è la stessa di quella tra B e A, ma lo spostamento è diverso a seconda del loro ordine.

Click è un termine gergale che indica un chilometro, ovvero 0,62 miglia. In realtà si scrive con la "k" (Klick) perché deriva dalla parola chilometro. È comunemente usato dai militari e dai motociclisti.

La formula della distanza è: √[(x₂ - x₁)² + (y₂ - y₁)²]. Questo funziona per due punti nello spazio 2D con coordinate (x₁, y₁) per il primo punto e (x₂, y₂) per il secondo punto. Puoi memorizzarlo facilmente se noti che si tratta del teorema di Pitagora e che la distanza è l'ipotenusa e le lunghezze dei cateti sono la differenza tra le componenti x e y dei punti.

La distanza di un vettore è la sua magnitudine. Se conosci le sue componenti:

1. Prendi ciascuna delle componenti del vettore e elevale al quadrato;
2. Somma il tutto;
3. Trova la radice quadrata del risultato precedente; e
4. Buon lavoro!

Se conosci la sua rappresentazione polare, sarà un numero e un angolo. Questo numero è la grandezza del vettore, ovvero la sua distanza.

L'unità di misura SI della distanza è il metro, abbreviato in "m". Altre unità comuni nel Sistema Internazionale sono il centimetro (un centesimo di metro, o 0,39 pollici) e il chilometro (mille metri o 0,62 miglia), tra le altre.

La distanza da A a B è la lunghezza della linea retta che va da A a B. La distanza da B ad A è uguale alla distanza da A a B perché la distanza è uno scalare

La distanza è una misura dello spazio monodimensionale. La distanza tra due punti è la lunghezza più breve dello spazio monodimensionale che li separa. Se si divide la distanza per il tempo si ottiene la velocità media, che ha dimensioni di spazio nel tempo.

L'anno luce è una misura di distanza. È pari a 9,461×10¹² chilometri, ovvero la distanza percorsa da un raggio di luce in un vuoto perfetto nell'arco di un anno.

Dalla velocità e dal tempo di spostamento di un oggetto puoi calcolare la distanza:

1. Assicurati che la velocità media e il tempo abbiano unità di misura compatibili (miglia all'ora e ore, metri al secondo e secondi);
2. Se non lo sono, convertili nelle unità necessarie;
3. Moltiplica la velocità per il tempo; e
4. Il risultato dovrebbe essere la distanza percorsa in qualsiasi unità di misura della velocità media!