Calculadora de Log (Logaritmo)

Esta calculadora de log (calculadora de logaritmo) da Omni permite que você calcule o logaritmo de um número (real positivo) com uma base escolhida (positiva definida e diferente de 1). Esta ferramenta irá resolver seu problema, independentemente se você quer calcular um logaritmo natural, um log de base 2 ou um log de base 10.

Continue lendo para entender melhor a função logarítmica e as propriedades do logaritmo. No texto, você poderá encontrar algumas informações interessantes, como o porquê dos logaritmos serem essenciais em nossas vidas e onde eles são aplicados. Após ler tudo, resolver exercícios de logaritmos será uma moleza!

Se você também estiver procurando outras calculadoras matemáticas úteis, não hesite em dar uma olhada na calculadora de raiz cúbica da Omni, que permite calcular não apenas a raiz cúbica, mas também raízes de qualquer grau.

Prefere assistir um vídeo ao invés de ler? Aprenda tudo o que você precisa em 90 segundos com este vídeo que fizemos para você:

Uma função logarítmica é o inverso da função exponencial. Para mais detalhes sobre a função exponencial veja a calculadora de função exponencial da Omni. Em essência, se a elevado à potência y resulta em x, então o logaritmo de x com base a é igual a y. Na forma de equação, aʸ = x é equivalente a logₐ(x) = y.

Em outras palavras, o logaritmo de x, ou logₐ(x), mostra qual é a potência que precisamos elevar a (ou, se x for maior que 1, quantas vezes a precisa ser multiplicado por ele mesmo), para produzir o valor x. A partir dessa abordagem, também podemos representar o logaritmo da seguinte forma:

$\mathrm{a^{{log}_a(x)}} =\mathrm x$

Agora a próxima vez que alguém perguntar “o que é um logaritmo?” esperamos que você possa responder num piscar de olhos! Na próxima seção, você poderá ler sobre as duas formas de representação utilizadas com mais frequência.

Você pode escolher vários números como base para logaritmos. Contudo, duas bases específicas são usadas com tanta frequência que os matemáticos deram nomes exclusivos a elas, o logaritmo natural (também conhecido como logaritmo neperiano) e o logaritmo comum.

Logaritmo natural

Se quiser calcular o logaritmo neperiano de um número, você precisará escolher uma base que seja aproximadamente igual a 2,718281. Convencionalmente, esse número é simbolizado por e, nomeado em homenagem a Leonard Euler, que definiu seu valor em 1731. Da mesma forma, o logaritmo pode ser representado como logₑx, que é tradicionalmente denotado com o símbolo ln(x). Você também pode ver a notação log(x), que se refere à mesma função, principalmente em finanças e economia. Portanto, y = logₑx = ln(x) que é equivalente a x = eʸ = exp(y).

Uma maneira prática de entender a função do logaritmo neperiano é colocá-la no contexto de juros compostos. Você pode calcular esses juros com a calculadora de juros compostos da Omni. Esses são os juros calculados sobre o juro principal e os juros acumulados.

A fórmula para os juros compostos anuais é a seguinte:

A = P(1 + r/m)ᵐᵗ

onde:

• A – É o valor do investimento após t anos;
• P – Representa o valor inicial;
• r – É a taxa de juros anual (em decimais);
• m – Representa o número de vezes que os juros são compostos por ano ou a frequência da composição; e
• t – Refere-se ao número de anos.

Vamos supor que você deposite algum dinheiro por um ano em um banco onde a composição ocorre com frequência, portanto m é um número grande. É fácil ver a rapidez com que o valor de m está aumentando se você comparar as frequências anual (m=1), mensal (m=12), diária (m=365) ou horária (m=8.760). Vamos imaginar que seu dinheiro é recalculado a cada minuto ou segundo. Neste caso, m se torna um número consideravelmente alto.

Agora, vamos verificar como a frequência da composição crescente afeta seu dinheiro inicial:

Você pode notar que, embora a frequência de composição atinja um número excepcionalmente alto, o valor de (1 + r/m)ᵐ (que é o multiplicador do seu depósito inicial) não aumenta muito. Em vez disso, ele tende para um valor estável, isto porque, ele está se aproximando de um valor único já mencionado acima, e ≈ 2,718281.

Como as taxas de crescimento geralmente seguem um padrão semelhante ao do exemplo acima, a economia também depende muito dos logaritmos naturais. Duas variáveis comuns envolvem o logaritmo natural: o crescimento do PIB 🇺🇸 e a elasticidade de preço da demanda.

Logaritmo comum

A outra forma popular de logaritmo é o logaritmo comum com base 10, log₁₀x, que é convencionalmente denotado como lg(x). Ele também é conhecido como logaritmo decimal, logaritmo decádico, logaritmo padrão ou logaritmo briggsiano, em homenagem a Henry Briggs, um matemático inglês que desenvolveu seu uso. Por vezes, ele também é denominado de log 10, embora este termo possa ser confuso, pois também pode se referir ao log₁₀10.

Como o nome sugere, é a forma de logaritmo usada com mais frequência. Ela é aplicada, por exemplo, em nossa calculadora de dB. As tabelas de logaritmos que tinham como objetivo facilitar o cálculo nos tempos antigos, também apresentavam logaritmos comuns.

A tabela abaixo representa alguns logaritmos comuns e naturais de números frequentes.

Se você tiver um exercício de logaritmo que envolve o cálculo de um logaritmo com uma base arbitrária, mas puder acessar apenas uma calculadora de logaritmo natural ou uma calculadora de base log 10, será necessário aplicar as seguintes regras:

• logₐ(x) = ln(x) / ln(a)
• logₐ(x) = lg(x) / lg(a)

Suponhamos que você queira usar esta calculadora de log para resolver um exercício de logaritmo que envolve o cálculo de um log de base 2. Para calcular o logaritmo de qualquer número, basta você seguir estas etapas simples:

1. Decida o número do qual você deseja encontrar o logaritmo. Digamos que seja 100.
2. Decida qual é a base que você quer usar, por exemplo, 2.
3. Encontre o logaritmo com base 10 do número 100, lg(100) = 2.
4. Encontre o logaritmo com base 10 do número 2, lg(2) = 0,30103.
5. Divida esses valores um pelo outro: lg(100)/lg(2) = 2 / 0,30103 = 6,644.
6. Você também pode pular as etapas 3 a 5 e inserir o número e a base diretamente na calculadora de log da Omni.

As evidências sugerem que a noção de logaritmos já estava presente na Índia no século VIII. Entretanto, o conceito mais amplo de logaritmo apareceu pela primeira vez no livro intitulado Mirifici logarithmorum canonis descriptio (A construção do maravilhoso método dos logaritmos), impresso em 1614. Esse livro foi o resultado de 20 anos de pesquisas do matemático escocês John Napier, com o objetivo de facilitar o cálculo dos logaritmos e aplicá-los em astronomia e física.

A primeira parte do livro explica de forma precisa a teoria, áreas de aplicação e propriedades do logaritmo. A segunda parte do livro possui noventa páginas de tabelas com exemplos de cálculos logarítmicos. Napier também enuncia as limitações de seu trabalho e fornece analogias, exemplos, avisos, lembretes e conclusões. Portanto, o livro funciona como um manual de instruções. No entanto, ele não detalha como a ferramenta foi criada.

Para nossa geração, pode não ser fácil, à primeira vista, apreciar a invenção do logaritmo, pois costumamos usar calculadoras, como esta calculadora de log, e computadores modernos. Entretanto, no século XVII, essa foi uma descoberta que afetou profundamente a vida das pessoas. A resolução de problemas matemáticos antes do surgimento dos logaritmos podia levar horas, dias ou até anos.

O primeiro avanço explícito que os logaritmos trouxeram foi o aprimoramento dos cálculos por meio da conversão da multiplicação e da divisão em adição e subtração. O único esforço adicional era procurar logaritmos e antilogaritmos em tabelas.

O novo procedimento de computação via logaritmos foi fundamental no campo da astronomia. As atividades científicas de Napier coincidiram com a era de novos desenvolvimentos na astrofísica. Como resultado, muitos astrônomos estavam lutando com cálculos intermináveis para detectar a posição dos planetas usando a teoria do sistema solar de Copérnico. Johannes Kepler, na época trabalhando em suas famosas leis de movimentos planetários, estava entre eles.

Graças ao esforço de Napier, ele pôde reduzir substancialmente sua carga de trabalho, que antes exigia cerca de mil páginas de cálculos, permitindo-lhe dedicar mais tempo a especulações filosóficas.

O famoso matemático britânico Henry Briggs percebeu rapidamente a capacidade da nova invenção: ele se mudou para a Escócia para conhecer Napier, para que pudessem começar a buscar possíveis avanços juntos.

Como resultado, após modificações no trabalho original, em 1617, eles formularam a primeira tabela de logaritmos baseada em potências de 10. Em 1624, após a morte de Napier, Briggs publicou seu livro, Arithmetica logarithmic, que apresentava tabelas de logaritmos para 30 mil números naturais com 14 casas decimais. Essa forma de logaritmos é considerada hoje como logaritmos comuns (Katrici, 2007).

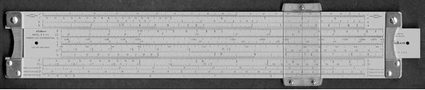
A crescente popularidade desse novo instrumento matemático estimulou outras explorações. Em 1620, Edmund Gunter apresentou a linha de cálculo do logaritmo, um dispositivo físico usado para multiplicações e divisões.

A versão inicial da ferramenta, que exigia um compasso para medição, foi desenvolvida por William Oughtred por volta de 1622. Ele projetou a regra de cálculo convencional, um dispositivo com duas réguas que deslizam uma ao lado da outra.

Dessa forma, ele criou uma nova abordagem para facilitar ainda mais a computação da lei do logaritmo. As réguas de cálculo se tornaram um dispositivo de computação padrão em profissões que exigiam aritmética. Arquitetos, engenheiros, cientistas e até mesmo astronautas contaram com seu auxílio até o advento da Revolução Digital. Albert Einstein utilizou uma dessas réguas, e as tripulações das missões Apollo também levaram réguas de cálculo para o espaço.

Em comparação com a versão inicial dos computadores, a régua de cálculo tinha muitas vantagens:

• Pequena o suficiente para ser guardada no bolso;
• Não requer uma fonte de energia;
• Relativamente barata;
• Mecanicamente confiável;
• Simples de funcionar; e
• Pode resolver diversos problemas numéricos.

Hoje em dia, os computadores modernos e as calculadoras científicas substituíram as práticas antigas. Ainda assim, entender os conceitos por trás dos logaritmos podem ajudar você a desenvolver suas habilidades matemáticas. Os logaritmos ainda têm vários usos práticos em muitos campos.

O fato dos logaritmos relacionarem a progressão aritmética com a progressão geométrica, sugere que certos fenômenos do mundo real podem formar um padrão logarítmico. De fato, há muitos exemplos na natureza e em nossa vida prática que podem ser atribuídos ao logaritmo mágico.

Por exemplo, os fenômenos naturais a seguir mostram uma espiral logarítmica:

• Concha de um nautilóide.

• Galáxias

• Ciclones

Além disso, há outros fenômenos medidos em escala logarítmica:

• Dureza mineral, Escala de Mohs;
• Intensidades de sons, Decibéis (dB);
• Intensidade do vento, Escala Beaufort;
• Terremotos, Escala Richter; e
• Acidez, pH.

Você sabia que o logaritmo ajuda a calcular o valor da figura de ruído 🇺🇸? Essa é uma medida significativa em áreas de estudo de redução e controle de ruído.

Antes do final da década de 1970, quando as calculadoras de bolso se tornaram acessíveis ao público em geral, a realização de cálculos, especialmente com frações, exigia um esforço manual considerável. Para aliviar esse trabalho tedioso, a aplicação de logaritmos tinha uma função prática.

Para utilizar suas vantagens técnicas, ter familiaridade com as propriedades do logaritmo é essencial. Provavelmente, você já conhece essas regras, mas, para te lembrar, a tabela abaixo as exibe de forma detalhada.

Para demonstrar como isso era útil nos tempos pré-calculadora, vamos supor que você precise calcular o produto de 5,89 ⋅ 4,73 sem nenhum dispositivo eletrônico. Você poderia fazer isso simplesmente multiplicando os números no papel, no entanto, isso levaria um pouco de tempo. Em vez disso, você pode usar a regra do logaritmo com tabelas de log e obter uma aproximação relativamente boa do resultado.

Se você tivesse uma tabela de logaritmos, poderia verificar rapidamente o logaritmo desses números (ou usar a Internet para encontrar uma tabela carregada eletronicamente), mas vamos trapacear um pouco e usar a calculadora de log da Omni para essa finalidade, resultando em:

$\text{lg}(5,\!89) ≅ 0,\!7701153$ e $\text{lg}(4,\!73) ≅ 0,\!674861$

Ao aplicar a primeira regra, podemos escrever a seguinte equação:

$\text{lg}(5,\!89 \cdot 4,\!73) =\text{lg}(5,\!89) + \text{lg}(4,\!73) ≅ 0,\!770115 + 0,\!6748611$

$\text{lg}(5,\!89 \cdot 4,\!73) ≅ 1,\!4449761$

Ainda não sabemos qual é o resultado exato, portanto, tomamos o expoente de ambos os lados da equação acima e consideramos uma manipulação adicional no lado direito, nos levando a:

$5,\!89 \cdot 4,\!73 ≅ 10^{1,\!4449761} = 10^{0,\!4449761} \cdot 10^1$

Agora, o que você precisa fazer é verificar quanto vale 10^0,4449761 em uma tabela antilog ou, alternativamente, verificar em nossa calculadora de antilog. Qual é o antilogaritmo de 0,4449761 na base 10? 2,785968.

Reescrevendo a equação:

$5,\!89 \cdot 4,\!73 ≅ 2,\!785968 \cdot 10^1 = 27,\!85968$

Provavelmente, o procedimento acima parece ser mais complexo em comparação com a simples digitação em uma calculadora de bolso ou o uso de qualquer aplicativo capaz de reproduzi-lo, como a nossa calculadora de log. Para mostrar como o poder dos logaritmos pode ajudar você mesmo em nossos tempos modernos, vamos considerar uma operação fatorial 🇺🇸 de 100, que é o produto de todos os inteiros de 1 a 100, dada por:

$100! = 1 \times 2 \times 3 \times 4 \times ⋯ \times 99 \times100$

Se você estivesse tentando resolver esse problema com uma calculadora de bolso comum, provavelmente não conseguiria, pois o resultado é um número enorme com muitos dígitos.

Mas com a ajuda dos logaritmos, você pode reescrever (com alguns arredondamentos) a operação como:

$\text{lg100!} = \text{lg1} + \text{lg2} + \text{lg3} + ⋯ + \text{lg100} = 0 + 0,\!30103 + 0,\!47712 + ⋯ + 2 ≅ 157,\!97$

$100! ≅ 10^{0,\!97} \cdot 10^{157} = 9,\!3325 \cdot 10^{157}$

Bem melhor, não é?