Omni Calculator logo
Última atualização:

Calculadora de Trajetória de Projétil

Novo

Índice

Definição de trajetóriaFórmula de trajetóriaCalculadora de trajetória de projétil: como usarPerguntas frequentes

Use a calculadora de trajetória de projétil da Omni para encontrar a trajetória de voo de um projétil. Digite três valores: velocidade, ângulo e altura inicial, e a ferramenta fornecerá a equação da trajetória e sua forma. Continue lendo se você quiser verificar a definição da trajetória, bem como um exemplo simples de aplicação.

Enquanto você estiver aqui, não deixe de conferir também nossa calculadora de movimento de projétil.

Definição de trajetória

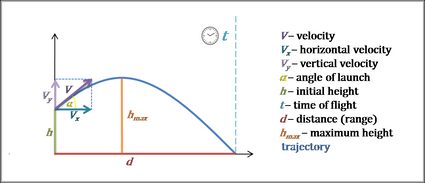
Trajetória, também chamada de trajetória de voo, é o caminho seguido por um objeto em movimento sob a ação da gravidade. Normalmente, usamos o termo quando falamos de projéteis ou satélites (onde a trajetória que se repete regularmente é chamada de órbita). Se você lançar um objeto por uma distância curta, uma parábola é uma boa aproximação do formato da trajetória.

Alguns exemplos de movimentos de projéteis são:

  • Disco de hóquei no gelo, bola de beisebol ou bola de golfe em voo ⚾.
  • Uma bala disparada de uma arma 🔫.
  • Um jato de água de uma fonte ⛲.
  • Gotas de sangue. (Por quê? Verifique nossa calculadora de ângulo de impacto 🇺🇸).
  • Um objeto lançado desde uma mesa/avião/edifício/ponte ✈️.

Fórmula de trajetória

Agora que você conhece a definição de trajetória, verifiquemos como é a equação da trajetória.

Imagem do movimento do projétil. Estão destacadas a velocidade, o ângulo de lançamento, a altura inicial, o tempo de voo, a distância e a altura máxima.
Imagem do movimento do projétil. Estão destacadas a velocidade (velocity), a velocidade horizontal (horizontal velocity), a velocidade vertical (vertical velocity), o ângulo de lançamento (angle of launch), a altura inicial (initial height), o tempo de voo (time of flight), a distância (distance) e a altura máxima (maximum height).

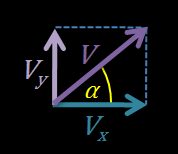
1. Vamos começar com as equações de movimento:

x=Vx⋅t\qquad x = V_x \cdot t
y=h+Vy⋅t−g⋅t22\qquad y = h +V_y \cdot t - \frac{g\cdot t^2}{2}

2. Podemos ver que os vetores V0V_0, VxV_x e VyV_y formam um triângulo retângulo, assim, escrevemos:

Velocidade e seus componentes horizontal e vertical

  • A componente horizontal da velocidade VxV_x é igual a V0⋅cos⁡(α)V_0\cdot \cos(\alpha).

  • A componente vertical da velocidade Vy=V0⋅sen(α)V_y= V_0\cdot {\rm sen}(\alpha).

3. Em seguida, combinamos as equações dos componentes de movimento e velocidade em uma única fórmula:

x=Vx⋅tt=xVx\qquad \begin{split} x &= V_x\cdot t\\ t & = \frac{x}{V_x} \end{split}

Portanto:

y=h+Vy⋅t−g⋅t22y=h+Vy⋅xVx−g⋅(xVx)22y=h+x⋅V0⋅sen(α)V0⋅cos⁡(α)−g⋅12⋅(xV0⋅cos⁡(α)) ⁣2\begin{split} y &= h +V_y \cdot t - \frac{g\cdot t^2}{2}\\[1.5em] y &= h +V_y \cdot \frac{x}{V_x} - \frac{g\cdot( \frac{x}{V_x})^2}{2}\\[1.5em] y &= h+x\cdot \frac{V_0\cdot {\rm sen}(\alpha)}{V_0\cdot \cos(\alpha)}\\[1.5em] &\quad-g\cdot\frac{1}{2}\cdot\left(\frac{x}{V_0\cdot\cos(\alpha)}\right)^{\!2} \end{split}

E, como sabemos, a razão do seno sobre o cosseno é a definição de tangente. Portanto, a versão final da equação da trajetória é:

y=h+x⋅tg(α)−g⋅x22⋅V02⋅cos⁡2(α)\begin{split} y &= h+x\cdot tg(\alpha)\\[1.5em] &-g\cdot \frac{x^2}{2\cdot V_0^2 \cdot\cos^2(\alpha)} \end{split}

Se você tiver interesse em diferentes aspectos do movimento de projéteis, confira outras ferramentas da Omni:

Calculadora de trajetória de projétil: como usar

Vamos verificar a trajetória da água de uma fonte:

Fonte de água. Exemplo de trajetória no movimento de projéteis
  1. Digite a velocidade. Suponha que ela seja igual a 1,5 m/s1{,}5\ \mathrm{m/s}.
  2. Digite o ângulo. Por exemplo, 60°60\degree.
  3. Escolha a altura inicial. Vamos escolher 13 cm13\ \mathrm{cm}.
  4. E pronto! A calculadora de trajetória de projétil exibe a fórmula e a trajetória de voo!

É possível que exista uma diferença na escala dos eixos, de modo que o ângulo não parece o que deveria ser no gráfico. Lembre-se de que, em todos os cálculos, a resistência do ar é desprezada.

Perguntas frequentes

Como encontrar o ângulo máximo no movimento do projétil?

Para encontrar o ângulo que maximiza a distância horizontal no movimento do projétil, siga as próximas etapas:

  1. Pegue a expressão para a distância horizontal percorrida: x = sen(2θ) ⋅ v²/g.
  2. Tome a derivada da expressão em relação ao ângulo: 2 ⋅ cos(2θ) ⋅ v²/g.
  3. Iguale o resultado do passo 2 a 0 e resolva para θ: o ângulo que dá 0 é 2θ = π/2; portanto, θ = π/4 = 45°.

Qual é a trajetória de um projétil lançado a 30° e 10 m/s?

Supondo um lançamento com altura inicial zero, a trajetória do projétil segue esta equação:

y = (x ⋅ tg(30°)) + (g ⋅ x²)/(2 ⋅ 10² ⋅ cos²(30°))

Qual é a forma da trajetória de um projétil?

A trajetória seguida por um projétil é uma parábola, portanto, uma equação quadrática na coordenada horizontal. Esse movimento é uma consequência da ação da força da gravidade: uma desaceleração na direção vertical transfere uma dependência quadrática do movimento vertical.

Como calcular a altura máxima de um projétil com θ = 40° e v₀=5 m/s?

Para calcular:

  1. Comece com a equação para o movimento vertical do projétil: y = vᵧ ⋅ t - g ⋅ t² / 2, onde vᵧ é a velocidade vertical inicial igual a vᵧ = v₀ ⋅ sen(θ) = 5 ⋅ sen(40°) = 3,21 m/s.

  2. Calcule o tempo necessário para atingir a altura máxima: ele corresponde ao tempo em que vᵧ = 0, e é igual a t = vᵧ/g = 3,21 / 9,81 = 0,327 s.

  3. Substitua os valores na equação:
    y = 3,21 ⋅ 0,327 - 9,81 ⋅ (0,327)² /2 = 0,525 m.

Fórmula da trajetória:

y = h + xtan(α) - gx²/2V₀²cos²(α)

Gráfico da trajetória de um projétil em movimento.
Check out 27 similar kinematics calculators — how things move ⏱️
Arrow speedBallistic coefficientCar jump distance...24 more