Calculadora de Altura Máxima - Movimento de Projétil

A calculadora de altura máxima é uma ferramenta Omni para encontrar a posição vertical máxima de um objeto lançado em movimento de projétil. Se você precisa da fórmula de altura máxima para um objeto lançado diretamente do solo ou a partir de alguma elevação inicial, nós temos o que você deseja. Se você continua se perguntando como encontrar a altura máxima de um projétil, leia os dois parágrafos abaixo e tudo ficará claro.

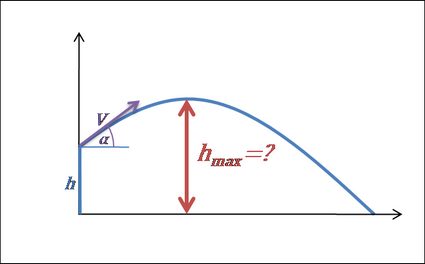
A altura máxima do objeto é a posição vertical mais alta ao longo de sua trajetória. O objeto está voando para cima antes de atingir o ponto mais alto. Em seguida, está caindo a partir desse ponto. Isso significa que, no ponto mais alto do movimento do projétil, a velocidade vertical é igual a $0$ ($v_y = 0$), resultando em:

A partir dessa equação, você pode encontrar o tempo $t_{\mathrm{h}}$ necessário para atingir a altura máxima $h_{\mathrm{max}}$:

A fórmula que descreve a posição vertical é a seguinte:

Portanto, considerando $y = h_{\mathrm{max}}$ e $t = t_{\mathrm{h}}$, podemos juntar essas duas equações, resultando em:

O que ocorre se lançarmos um projétil de alguma altura inicial $h$? Não se preocupe! O procedimento é muito fácil, tudo o que você precisa fazer é adicionar essa elevação inicial na equação para a altura máxima!

Vamos discutir alguns casos especiais com a alteração do ângulo de lançamento:

• Se $\alpha = 90\degree$, então, a fórmula se simplifica para:

Neste caso, o tempo de voo é o mais longo.

Se, além disso, $v_y = 0$, então, temos o caso de um objeto em queda livre, que detalhamos na calculadora de queda livre da Omni. Além disso, se você quiser entender um lançamento mais realista, não deixe de acessar a nossa calculadora de queda livre com resistência do ar 🇺🇸.

• Se $\alpha = 45\degree$, então, a equação pode ser escrita como:

Nesse caso, o alcance é máximo se você fizer o lançamento do solo ($h = 0$).

• Caso você considere $\alpha = 0\degree$, a velocidade vertical será igual a $0$ ($v_y = 0$). Nesse cenário, podemos calcular o movimento horizontal do projétil. Como o seno de $0\degree$ é $0$, a segunda parte da equação desaparece e você obtém:

A altura inicial da qual estamos lançando o objeto é a altura máxima no movimento do projétil.

O movimento de um projétil é um problema clássico da física e foi analisado em todos os aspectos possíveis. O fato de podermos reproduzi-lo e observá-lo facilmente foi um fator que contribuiu para isso. Decidimos criar um conjunto de ferramentas relacionadas ao movimento de um projétil, como a:

• Calculadora de movimento de projétil para uma análise abrangente do problema;

• Calculadora de trajetória para analisar o problema como uma função geométrica; e

• Assim como um conjunto de ferramentas específicas, como a:

  • Calculadora de alcance de projétil 🇺🇸;
  • Calculadora de tempo de voo - movimento de projétil 🇺🇸; e
  • Calculadora de movimento horizontal de projétil (para $\alpha=0$).

Observe como esta calculadora de altura máxima é fácil de usar:

1. Escolha a velocidade do projétil. Vamos digitar $9\ \mathrm{m/s}$.

2. Digite o ângulo. Suponha que estejamos chutando uma bola ⚽ em um ângulo de $70\degree$.

3. Opcionalmente, digite a altura inicial. No nosso caso, nossa posição inicial é o chão, portanto, digite $0$. A bola pode passar por cima de uma cerca de $4\ \mathrm{m}$?

4. E pronto, a calculadora de altura máxima exibe a resposta! A altura máxima da bola será $3{,}65\ \mathrm{m}$. Portanto, ela não voará sobre a barreira mencionada. Para atingir o seu objetivo, você pode aumentar a velocidade de lançamento ou o ângulo.

Lembre-se de que neste caso, não levamos em conta a resistência do ar!