Calculadora de Movimento de Projétil

A calculadora de movimento de projétil da Omni é uma ferramenta que ajuda você a analisar o movimento de projéteis em trajetórias parabólicas. Com ela, você pode encontrar o tempo de voo, as componentes da velocidade, o alcance do projétil e a altura máxima de voo. Continue lendo se você quiser entender o que é movimento de um projétil, familiarizar-se com a definição de movimento de projéteis e determinar os valores mencionados acima usando as equações de movimento de projéteis.

Prefere assistir um vídeo a ler? Aprenda tudo o que precisa em 90 segundos com este vídeo que fizemos para você:

Imagine um arqueiro lançando uma flecha no ar. Ela começa a se mover para cima e para frente, com uma certa inclinação em relação ao solo. Quanto mais ela voa, mais lenta é sua subida e, finalmente, ela começa a descer, movendo-se agora para baixo e para frente e, finalmente, atingindo o solo novamente. Se você pudesse traçar seu caminho, ele seria uma curva chamada trajetória parabólica. Qualquer objeto que se mova dessa forma caracteriza o movimento de projétil. A propósito, a Omni também tem a calculadora de velocidade de flecha, que analisa o movimento de flechas, experimente!

Apenas uma força atua em um projétil: a força da gravidade. A resistência do ar é sempre omitida. Se você desenhasse um diagrama de corpo livre desse objeto, só precisaria desenhar um vetor descendente e denotá-lo como "gravidade". Se houvesse qualquer outra força agindo sobre o corpo, então, pela definição de movimento de projétil, ele não seria um projétil.

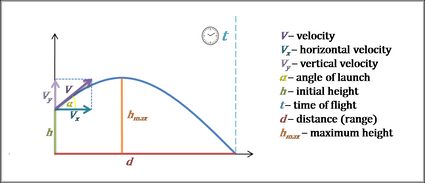
O movimento de projéteis é bastante lógico. Vamos supor que você saiba a velocidade inicial do objeto $V$, o ângulo de lançamento $\alpha$ e a altura inicial $h$. Nossa calculadora de movimento de projéteis segue essas etapas para que você encontre todos os parâmetros restantes:

1. Calcule as componentes do vetor velocidade.

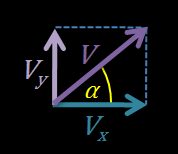
• A componente horizontal da velocidade $V_\mathrm x$ é igual a $V \cdot \cos\alpha$.
• A componente vertical da velocidade $V_\mathrm y$ é igual a $V \cdot \mathrm{sen}\,\alpha$.
• Os três vetores: $V$, $V_\mathrm x$ e $V_\mathrm y$ formam um triângulo retângulo.

Se a componente vertical da velocidade for igual a 0, então temos o movimento horizontal do projétil. Se, por outro lado, α = 90°, então, temos uma queda livre. Nós também abordamos esses cenários na calculadora de movimento horizontal de projétil e na calculadora de queda livre da Omni.

2. Escreva as equações de movimento.

Distância

• A distância horizontal percorrida pode ser expressa como $x = V_\mathrm x \cdot t$, onde $t$ é o tempo.
• A distância vertical do solo é descrita pela fórmula $y = h + V_\mathrm{y0} \cdot t - g \cdot t^2 / 2$, onde $g$ é a aceleração da gravidade e $V_\mathrm{y0}$ é a velocidade vertical inicial.

Velocidade

• A velocidade horizontal é igual a $V_\mathrm x$.
• A velocidade vertical pode ser expressa como $V_\mathrm y = V_\mathrm{y0} - g \cdot t$.

Aceleração

• A aceleração horizontal é igual a 0.
• A aceleração vertical é igual a $-g$ (porque somente a gravidade atua sobre o projétil).

3. Calcule o tempo de voo.

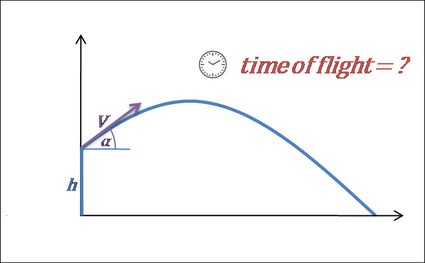
• O voo termina quando o projétil atinge o solo. Podemos dizer que isso acontece quando a distância vertical do solo é igual a 0. No caso em que a altura inicial é 0, a fórmula pode ser escrita como: $V_\mathrm{y0}\cdot t - g \cdot t^2 / 2 = 0$. Então, a partir dessa equação, descobrimos que o tempo de voo é:

• No entanto, se estivermos jogando o objeto de alguma elevação, a fórmula não será tão simples quanto antes, e teremos uma equação quadrática para resolver: $h + V_\mathrm{y0} \cdot t - g \cdot t^2 / 2 = 0$. Após resolvermos essa equação, obtemos:

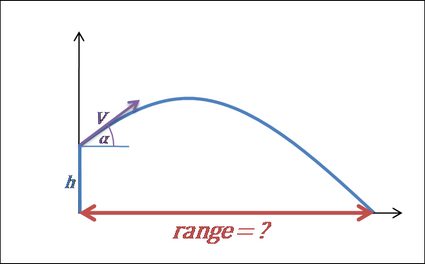
4. Calcule o alcance do projétil.

• O alcance do projétil é a distância horizontal total percorrida durante o tempo de voo. Novamente, se estivermos lançando o objeto do solo (altura inicial = 0), poderemos escrever a fórmula como $d = V_\mathrm x \cdot t = V_\mathrm x \cdot 2 \cdot V_\mathrm{y0} / g$. Ela também pode ser transformada na forma: $d = V^2_0 \cdot \mathrm{sen}\,(2\alpha) / g$

• As coisas ficam mais complicadas se considerarmos uma elevação inicial diferente de 0. Neste caso, precisamos substituir o tempo de voo $t$ na fórmula do alcance:

• O alcance é especialmente importante na balística. Falamos sobre isso com mais detalhes na calculadora de coeficiente balístico 🇺🇸 da Omni.

5. Calcule a altura máxima.

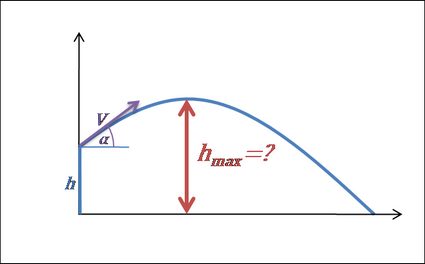
• Quando o projétil atinge a altura máxima, ele para de se mover para cima e começa a cair. Isso significa que sua componente vertical da velocidade muda de positiva para negativa, além de ser igual a 0 por um breve instante de tempo $t(V_\mathrm y=0)$.
• Se $V_\mathrm {y0} - g \cdot t(V_\mathrm y=0) = 0$, então, podemos reescrever esta equação como $t(V_\mathrm y=0) = V_\mathrm{y0} / g$.
• Agora, basta encontrarmos a distância vertical do solo naquele momento:

• Felizmente, no caso do lançamento de um projétil de alguma altura inicial $h$, precisamos simplesmente adicionar esse valor à fórmula final:

Ufa, foram muitos cálculos! Vamos resumir tudo isso escrevendo as equações de movimento de projéteis mais essenciais:

1. Lançamento do objeto a partir do solo (altura inicial h = 0):

• Componente horizontal da velocidade: $V_\mathrm x = V_0 \cdot \cos \alpha$
• Componente vertical da velocidade: $V_\mathrm y = V_0 \cdot \mathrm{sen}\, \alpha - g\cdot t$
• Tempo de voo: $t = 2 \cdot V_\mathrm{y0} / g$
• Alcance do projétil: $d = 2 \cdot V_\mathrm x \cdot V_\mathrm{y0} / g$
• Altura máxima: $h_\mathrm{max} = V^2_\mathrm{y0} / (2 g)$

2. Lançamento do objeto de alguma elevação (altura inicial h > 0):

• Componente horizontal da velocidade : $V_\mathrm x = V_0 \cdot \cos \alpha$
• Componente vertical da velocidade: $V_\mathrm y = V _0 \cdot \mathrm{sen}\, \alpha - g\cdot t$
• Tempo de voo: $t = \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 \cdot g \cdot h}\right] / g$
• Alcance do projétil: $d = V_\mathrm x \cdot \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 \cdot g \cdot h}\right] / g$
• Altura máxima: $h_\mathrm{max} = h + V^2_ \mathrm{y0} / (2 g)$

Com a nossa calculadora de movimento de projéteis, você certamente economizará muito tempo. Ela também pode funcionar "ao contrário". Por exemplo, insira o tempo de voo, a distância e a altura inicial e veja como ela faz todos os cálculos para você!

Não deixe de conferir também a calculadora de parábola da Omni, para saber mais sobre essa curva do ponto de vista matemático.