Calculadora de Valor Crítico

Bem-vindo à calculadora de valor crítico da Omni! Aqui, você pode determinar rapidamente o(s) valor(es) crítico(s) para testes bicaudais, bem como para testes unicaudais. Ela funciona para as distribuições mais comuns em testes estatísticos: a distribuição normal padrão N(0,1) (que é quando você tem um escore-z), t-Student, qui-quadrado e distribuição F.

O que é um valor crítico? Qual é a fórmula do valor crítico? Role para baixo, pois fornecemos a você a definição de valor crítico e explicamos como calcular valores críticos para usá-los na construção de regiões de rejeição (também conhecidas como regiões críticas).

No teste de hipóteses, os valores críticos são uma das duas abordagens que permitem que você decida se deve manter ou rejeitar a hipótese nula. A outra abordagem é calcular o valor-p (por exemplo, usando a calculadora de valor-p da Omni).

A abordagem do valor crítico consiste em verificar se o valor da estatística de teste gerada pela sua amostra pertence à chamada região de rejeição ou região crítica, sendo esta a região onde é altamente improvável que a estatística de teste se encontre. Um valor crítico é um valor de corte (ou dois valores de corte no caso de um teste bicaudal) que constitui o limite da(s) região(ões) de rejeição. Em outras palavras, os valores críticos dividem a escala da estatística do seu teste na região de rejeição e na região de não rejeição.

Depois que você tiver encontrado a região de rejeição, verifique se o valor da estatística de teste gerado pela sua amostra pertence a ela:

• Em caso afirmativo, isso significa que você pode rejeitar a hipótese nula e aceitar a hipótese alternativa; e
• Se não, então não há evidência suficiente para que você rejeite H₀.

Mas como calcular os valores críticos? Em primeiro lugar, você precisa definir um nível de significância, $\alpha$, que quantifica a probabilidade de rejeitar a hipótese nula quando ela estiver realmente correta. A escolha de α é arbitrária. Na prática, geralmente usamos um valor de 0,05 ou 0,01. Os valores críticos também dependem da hipótese alternativa que você escolher para o teste, abordada na próxima seção intitulada "Definição de valor crítico".

Para determinar os valores críticos, você precisa conhecer a distribuição da estatística de teste sob a suposição de que a hipótese nula seja válida. Os valores críticos são então pontos com a propriedade de que a probabilidade de sua estatística de teste assumir valores pelo menos tão extremos quanto esses valores críticos, é igual ao nível de significância α. Uau, uma definição e tanto, não é mesmo? Não se preocupe, explicaremos a você o que tudo isso significa.

Em primeiro lugar, devemos observar que é a hipótese alternativa que determina o que significa "extremo". Em particular, se o teste for unilateral (ou unicaudal), haverá apenas um valor crítico; se for bilateral (ou bicaudal), haverá dois deles: um à esquerda e outro à direita do valor mediano da distribuição.

Os valores críticos podem ser convenientemente representados como os pontos com a propriedade de que a área sob a curva de densidade da estatística de teste desses pontos até as caudas é igual a $\alpha$:

• Teste de cauda esquerda: a área sob a curva de densidade do valor crítico à esquerda é igual a $\alpha$;

• Teste de cauda direita: a área sob a curva de densidade do valor crítico à direita é igual a $\alpha$; e

• Teste bicaudal: a área sob a curva de densidade do valor crítico da esquerda para a esquerda é igual a $\alpha/2$, e a área sob a curva do valor crítico da direita para a direita também é igual a $\alpha/2$; portanto, a área total é igual a $\alpha$.

Como você pode ver, encontrar os valores críticos para um teste bicaudal com significância $\alpha$ se resume a encontrar os dois valores críticos unicaudais com um nível de significância de $\alpha/2$.

As fórmulas para os valores críticos envolvem o quantil, $Q$, que é o inverso da função de distribuição acumulada ($\mathrm{fda}$), para a distribuição estatística do teste (calculada sob a suposição de que H₀ é válido!): $Q = \mathrm{fda}^{-1}$.

Uma vez que tenhamos concordado com o valor de $\alpha$, as fórmulas de valor crítico são as seguintes:

1. Teste de cauda esquerda:

2. Teste de cauda direita:

3. Teste bicaudal:

No caso de uma distribuição simétrica em relação a 0, os valores críticos do teste bicaudal também são simétricos:

Infelizmente, as distribuições de probabilidade mais comuns nos testes de hipóteses têm fórmulas $\mathrm{fda}$ um tanto complicadas. Para encontrar os valores críticos manualmente, você precisaria usar um software especializado ou tabelas estatísticas. Nesses casos, a melhor opção é, obviamente, nossa calculadora de valores críticos! 😁

Agora que você encontrou a nossa calculadora de valor crítico, não precisa mais se preocupar em como determinar o valor crítico para todas essas distribuições complicadas! Aqui estão as etapas que você precisa seguir:

1. Informe-nos a distribuição da estatística de teste sob a hipótese nula: é uma distribuição normal padrão N(0,1), t-Student, qui-quadrado ou F de Snedecor? Se não tiver certeza, verifique as seções abaixo dedicadas a essas distribuições e tente localizar o teste que você precisa executar.

2. Escolha a hipótese alternativa: bicaudal, de cauda direita ou de cauda esquerda.

3. Se necessário, especifique os graus de liberdade da distribuição da estatística de teste. Se não tiver certeza, verifique a descrição do teste que você está realizando. Você pode saber mais sobre o significado dessa quantidade em estatística na calculadora de graus de liberdade da Omni.

4. Defina o nível de significância, $\alpha$. Nós o predefinimos para o valor mais comum, 0,05, por padrão, mas você pode, é claro, ajustá-lo às suas necessidades.

5. A calculadora de valor crítico exibirá não apenas o(s) valor(es) crítico(s), mas também a(s) região(ões) de rejeição.

Vá para o modo avançado da calculadora de valor crítico se você precisar aumentar a precisão com a qual os valores críticos são calculados.

Use a opção Z (escore padrão) se a estatística de teste seguir (aproximadamente) a distribuição normal padrão N(0,1).

Nas fórmulas abaixo, $u$ denota o quantil da distribuição normal padrão N(0,1):

1. Valor crítico Z de cauda esquerda: $u(\alpha)$

2. Valor crítico Z de cauda direita: $u(1-\alpha)$

3. Valor crítico Z bicaudal: $\pm u(1- \alpha/2)$

Consulte a calculadora de teste Z da Omni para saber mais sobre o teste Z, sendo este muito utilizado em dados que envolvem a média da população. Há também testes Z envolvendo duas médias populacionais, os quais são baseados no método da diferença entre duas proporções.

Use a opção t-Student se a estatística de teste seguir a distribuição t-Student. Essa distribuição é semelhante à N(0,1), mas suas caudas são mais grossas. Além disso, sua forma exata depende do número de graus de liberdade. Se esse número for grande (>30), o que geralmente ocorre em amostras grandes, a distribuição t-Student é praticamente indistinguível da N(0,1). Consulte a calculadora de valor t da Omni para calcular a estatística deste teste específico.

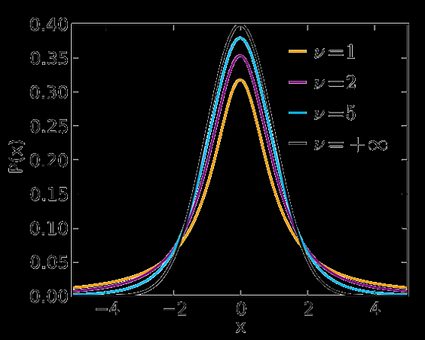
Nas fórmulas abaixo, $Q_{\text{t}, d}$ é o quantil da distribuição t-Student com $d$ graus de liberdade:

1. Valor crítico t de cauda esquerda: $Q_{\text{t}, d}(\alpha)$

2. Valor crítico t de cauda direita: $Q_{\text{t}, d}(1 - \alpha)$

3. Valores críticos t bicaudais: $\pm Q_{\text{t}, d}(1 - \alpha/2)$

Visite a calculadora de teste t da Omni para saber mais sobre vários testes t: aquele para uma média populacional com um desvio padrão populacional desconhecido, aqueles para a diferença entre as médias de duas populações (com desvios padrão populacionais iguais ou desiguais), bem como sobre o teste para amostras pareadas.

Use a opção χ² (qui-quadrado) ao executar um teste no qual a estatística de teste segue a distribuição χ².

Você precisa determinar o número de graus de liberdade da distribuição χ² da sua estatística de teste. Abaixo, listamos os graus de liberdade para os testes χ² mais usados.

Veja abaixo as fórmulas para os valores críticos do qui-quadrado. Aqui, $Q_{\chi^2, d}$ é o quantil da distribuição χ² com $d$ graus de liberdade:

1. Valor crítico χ² de cauda esquerda: $Q_{\chi^2, d}(\alpha)$

2. Valor crítico χ² de cauda direita: $Q_{\chi^2, d}(1 - \alpha)$

3. Valores críticos χ² bicaudais: $Q_{\chi^2, d}(\alpha/2)$ e $Q_{\chi^2, d}(1 - \alpha/2)$

Vários testes diferentes levam a um χ²-escore:

• Teste de adequação: a distribuição empírica está de acordo com a distribuição esperada?

  Esse teste é de cauda direita. Sua estatística de teste segue a distribuição χ² com $k - 1$ graus de liberdade, onde $k$ é o número de classes em que a amostra está dividida.

• Teste de independência: existe uma relação estatisticamente significativa entre duas variáveis?

  Esse teste também é de cauda direita e sua estatística de teste é calculada a partir da tabela de contingência. Há $(r - 1)(c - 1)$ graus de liberdade, em que $r$ é o número de linhas e $c$ é o número de colunas na tabela de contingência.

• Teste para a variância de dados normalmente distribuídos: essa variância tem algum valor predeterminado?

  Este teste pode ser unicaudal ou bicaudal! Sua estatística de teste tem a distribuição χ² com $n - 1$ graus de liberdade, em que $n$ é o tamanho da amostra.

Por fim, escolha F (Fisher-Snedecor) se a estatística de teste seguir a distribuição F. Essa distribuição tem um par de graus de liberdade.

Vamos ver como esses graus de liberdade surgem. Suponha que você tenha duas variáveis aleatórias independentes, $X$ e $Y$, que seguem distribuições χ² com graus de liberdade $d_1$ e $d_2$, respectivamente. Se você considerar agora a razão $(\frac{X}{d_1}):(\frac{Y}{d_2})$, verá que ela segue a distribuição F com $(d_1, d_2)$ graus de liberdade. Essa é a razão pela qual chamamos $d_1$ e $d_2$ de numerador e denominador de graus de liberdade, respectivamente.

Nas fórmulas abaixo, $Q_{\text{F}, d_1, d_2}$ representa o quantil da distribuição F com $(d_1, d_2)$ graus de liberdade:

1. Valor crítico F de cauda esquerda: $Q_{\text{F}, d_1, d_2}(\alpha)$

2. Valor crítico F de cauda direita: $Q_{\text{F}, d_1, d_2}(1 - \alpha)$

3. Valores críticos F bicaudais: $Q_{\text{F}, d_1, d_2}(\alpha/2)$ e $Q_{\text{F}, d_1, d_2}(1 -\alpha/2)$

Aqui listamos os testes mais importantes que produzem pontuações F: cada um deles é de cauda direita.

• ANOVA: testa a igualdade de médias em três ou mais grupos provenientes de populações normalmente distribuídas com variâncias iguais. Há $(k - 1, n - k)$ graus de liberdade, em que $k$ é o número de grupos e $n$ é o tamanho total da amostra (em cada grupo).

• Significância geral na análise de regressão. A estatística de teste tem $(k - 1, n - k)$ graus de liberdade, em que $n$ é o tamanho da amostra e $k$ é o número de variáveis (incluindo o ponto de interseção).

• Compare dois modelos de regressão aninhados. A estatística de teste segue a distribuição F com $(k_2 - k_1, n - k_2)$ graus de liberdade, em que $k_1$ e $k_2$ são o número de variáveis nos modelos menor e maior, respectivamente, e $n$ é o tamanho da amostra.

• A igualdade de variâncias em duas populações normalmente distribuídas. Há $(n - 1, m - 1)$ graus de liberdade, em que $n$ e $m$ são os respectivos tamanhos de amostra.

Um valor crítico Z é o valor que define a região crítica no teste de hipóteses quando a estatística de teste segue a distribuição normal padrão. Se o valor da estatística de teste cair na região crítica, você deve rejeitar a hipótese nula e aceitar a hipótese alternativa.

Para encontrar um valor crítico Z com um determinado nível de confiança α:

1. Verifique se você realiza um teste unicaudal ou bicaudal.

2. Para um teste unicaudal:

   • Teste de cauda esquerda: o valor crítico é o α-ésimo quantil da distribuição normal padrão N(0,1).

   • Cauda direita: o valor crítico é o (1-α)-ésimo quantil.

3. Teste bicaudal: o valor crítico é igual ao ±(1-α/2)-ésimo quantil de N(0,1).

4. Você não tem tabelas de quantis? Use tabelas da função distribuição acumulada! A função quantil é a inversa da função de distribuição acumulada.

5. Verifique sua resposta com uma calculadora de valor crítico on-line.

Em teoria, não. Na prática, com muita frequência, sim. A distribuição t-Student é semelhante à distribuição normal padrão, mas não é a mesma. No entanto, se o número de graus de liberdade (que é, a grosso modo, o tamanho da sua amostra) for grande o suficiente (>30), as duas distribuições serão praticamente indistinguíveis e, portanto, o valor crítico t terá praticamente o mesmo valor que o valor crítico Z.

O valor crítico Z para um intervalo de confiança de 95% é:

• 1,96 para um teste bicaudal;
• 1,64 para um teste de cauda direita; e
• -1,64 para um teste de cauda esquerda.