Calculadora de Teste Z

A calculadora de teste Z da Omni é uma ferramenta que ajuda você a realizar um teste Z de uma amostra na média da população. Existem duas formas de fazer esse teste: o teste Z bicaudal e o teste Z unicaudal. Ambos podem ser usados de acordo com suas necessidades. Você também pode escolher se a calculadora deve determinar o valor p (também conhecido como p-valor) do teste Z ou se prefere usar a abordagem do valor crítico!

Continue lendo para saber mais sobre o teste Z em estatística e, em particular, quando usar o teste Z, qual é a fórmula do teste Z e se você deve usar o teste Z ou o teste t. Como bônus, damos alguns exemplos passo a passo de como realizar testes Z!

Ou você também pode consultar outras ferramentas Omni, como a calculadora de valor T, onde poderá aprender o conceito de outro teste estatístico essencial. Ou ainda, se você também tiver interesse no teste F, consulte a calculadora de teste F 🇺🇸.

O teste Z de uma amostra é um dos testes estatísticos mais populares. A hipótese nula é que o valor médio da população é igual a um determinado número, $\mu_0$:

Realizamos um teste Z de duas caudas se quisermos testar se a média da população não é $\mu_0$:

e um teste Z unicaudal se quisermos testar se a média da população é menor/maior que $\mu_0$:

Vamos agora discutir as premissas de um teste Z para uma amostra.

Você pode usar um teste Z se sua amostra consistir em pontos de dados independentes e:

• os dados forem normalmente distribuídos, e você conhecer a variância da população;

  ou

• a amostra for grande e os dados seguirem uma distribuição que tenha uma média e uma variância finitas. Você não precisa conhecer a variância da população nesse caso.

O motivo pelo qual essas duas possibilidades existem é que queremos que as estatísticas de teste sigam a distribuição normal padrão $\mathrm N(0, 1)$. No primeiro caso, é uma distribuição normal padrão exata, enquanto no segundo, é aproximada, e pode ser usada pelo príncipio do teorema do limite central.

A pergunta que fica é: "Quando minha amostra é considerada grande o suficiente? " Bem, não há um critério universal. Em geral, quanto mais dados você tiver, melhor será o resultado da aproximação. Os livros didáticos de estatística recomendam que você tenha não menos que 50 dados, no entanto, 30 é considerado o menor valor possível.

Seja $x_1, ..., x_n$ uma amostra independente que segue a distribuição normal $\mathrm N(\mu, \sigma^2)$, ou seja, com uma média igual a $\mu$ e uma variação igual a $\sigma ^2$.

Colocamos a hipótese nula, $\mathrm H_0 \!\!:\!\! \mu = \mu_0$.

Definimos a estatística de teste, Z, como:

onde:

• $\bar x$ é a média da amostra, ou seja, $\bar x = (x_1 + ... + x_n) / n$;

• $\mu_0$ é a média da população em $\mathrm H_0$;

• $n$ é o tamanho da amostra; e

• $\sigma$ é o desvio padrão da população.

A seguir, a letra maiúscula $Z$ representa a estatística de teste (tratada como uma variável aleatória), enquanto a letra minúscula $z$ denota um valor real de $Z$, calculado para uma determinada amostra extraída de N(μ,σ²).

Se $\mathrm H_0$ for válida, então a soma $S_n = x_1 + ... + x_n$ segue a distribuição normal, com média $n \mu_0$ e variância $n^2 \sigma$. Como $Z$ é a padronização (escore z) de $S_n/n$, podemos concluir que a estatística de teste $Z$ segue a distribuição normal padrão $\mathrm N(0, 1)$, desde que $\mathrm H_0$ seja verdadeira. A propósito, temos a calculadora de escore padrão Z se você quiser se concentrar somente nesse valor.

Se nossos dados não seguirem uma distribuição normal ou se o desvio padrão da população for desconhecido (e, portanto, na fórmula para $Z$, substituímos o desvio padrão da população $\sigma$ pelo desvio padrão da amostra), então a estatística de teste $Z$ não segue necessariamente uma distribuição normal. Entretanto, se a amostra for suficientemente grande, o teorema do limite central garante que $Z$ é aproximadamente $\mathrm N(0, 1)$.

Nas seções abaixo, explicaremos a você como usar o valor da estatística de teste, $z$, para tomar uma decisão, ou seja, se você deve ou não rejeitar a hipótese nula. Duas abordagens podem ser usadas para que você chegue a essa decisão: a abordagem do valor p e a abordagem do valor crítico (abordaremos as duas!) Qual delas você deve usar? No passado, a abordagem do valor crítico era mais popular porque era difícil calcular o valor p do teste Z. Entretanto, com a ajuda dos computadores modernos, podemos fazer isso com bastante facilidade e com uma precisão decente. Em geral, é altamente recomendável que você informe o valor p dos seus testes!

Formalmente, o valor p é o menor nível de significância em que a hipótese nula pode ser rejeitada. Mais intuitivamente, o valor p responde às perguntas:
desde que eu viva em um mundo em que a hipótese nula seja válida, qual é a probabilidade de que o valor da estatística de teste seja pelo menos tão extremo quanto o $z$, valor que obtive para minha amostra? Portanto, um valor p pequeno significa que seu resultado é muito improvável sob a hipótese nula e, portanto, há fortes evidências contra a hipótese nula, quanto menor o valor p, mais forte é a evidência.

Para encontrar o valor p, você precisa calcular a probabilidade de que a estatística de teste, $Z$, seja pelo menos tão extrema quanto o valor que realmente observamos, $z$, desde que a hipótese nula seja verdadeira. (A probabilidade de um evento calculada sob a premissa de que $\mathrm H_0$ seja verdadeira será denotada como $\small \mathrm{Prob}(\text{evento} | \mathrm{H_0})$). É a hipótese alternativa que determina o que significa mais extremo:

1. Teste Z bicaudal: valores extremos são aqueles cujo valor absoluto excede $|z|$, portanto, menores que $-|z|$ ou maiores que $|z|$. Portanto, temos:

A simetria da distribuição normal fornece:

2. Teste Z de cauda esquerda: valores extremos são aqueles menores que $z$, portanto:

3. Teste Z de cauda direita: valores extremos são aqueles maiores que $z$, portanto:

Para calcular essas probabilidades, podemos usar a Função de Distribuição Acumulada (fda) de $\mathrm N(0, 1)$, que, para um número real, $x$, é definida como:

Além disso, os valores de p podem ser bem representados como a área sob a função de densidade de probabilidade de $\mathrm N(0, 1)$, devido a:

Com todo o conhecimento obtido na seção anterior, você está pronto para aprender sobre os testes Z.

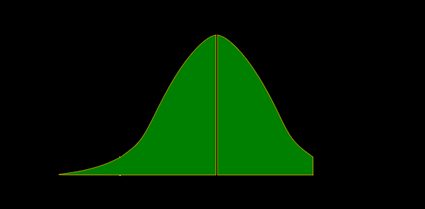
1. Teste Z bicaudal:

Do fato de que $\Phi(-z) = 1 - \Phi(z)$, deduzimos que:

O valor p é a área sob a função de distribuição de probabilidade à esquerda de $-|z|$ e à direita de $|z|$:

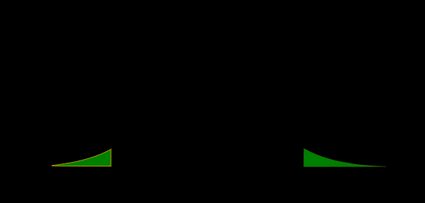
2. Teste Z de cauda esquerda:

O valor p é a área sob a função de densidade de probabilidade à esquerda de nosso $z$:

3. Teste Z de cauda direita:

O valor p é a área sob a função de densidade de probabilidade à direita de $z$:

A decisão de rejeitar ou não a hipótese nula pode ser tomada agora em qualquer nível de significância, $\alpha$, que você desejar!

• se o valor p for menor ou igual a $\alpha$, a hipótese nula será rejeitada nesse nível de significância; e

• se o valor p for maior que $\alpha$, então não há evidência suficiente para rejeitar a hipótese nula nesse nível de significância.

A abordagem do valor crítico envolve a comparação do valor da estatística de teste obtida para nossa amostra, $z$, com os chamados valores críticos. Esses valores constituem os limites das regiões em que é altamente improvável que a estatística de teste se encontre. Essas regiões são frequentemente chamadas de regiões críticas ou regiões de rejeição. A decisão de se você deve ou não rejeitar a hipótese nula é baseada no fato de o nosso $z$ pertencer ou não à região crítica.

As regiões críticas dependem de um nível de significância, $\alpha$, do teste e da hipótese alternativa. A escolha de $\alpha$ é arbitrária; na prática, os valores de 0,1, 0,05 ou 0,01 são mais comumente usados como $\alpha$.

Quando concordamos com o valor de $\alpha$, podemos determinar facilmente as regiões críticas do teste Z:

1. Teste Z bicaudal:

2. Teste Z de cauda esquerda:

3. Teste Z de cauda direita:

Para decidir o destino de $\mathrm H_0$, verifique se o seu $z$ está ou não na região crítica:

• Em caso afirmativo, rejeite $\mathrm H_0$ e aceite $\mathrm H_1$; e

• Se não, então não há evidência suficiente para rejeitar $\mathrm H_0.$

Como você pode ver, as fórmulas para os valores críticos dos testes Z envolvem o inverso, $\Phi^{-1}$, da função de distribuição acumulada (fda) de $\mathrm N(0, 1)$.

Nossa calculadora reduz todas as etapas complicadas:

1. Escolha a hipótese alternativa: bicaudal ou de cauda esquerda/direita.

2. Em nossa calculadora de teste Z, você pode decidir se quer usar o valor p ou a abordagem de regiões críticas. No último caso, defina o nível de significância, $\alpha$.

3. Digite o valor da estatística de teste, $z$. Se não souber, você pode inserir alguns dados que nos permitirão calcular o $z$ para você:

   • média da amostra $\bar x$ (se você tiver dados brutos, use a calculadora de média da Omni para determinar a média);
   • média testada $\mu_0$;
   • tamanho da amostra $n$; e
   • desvio padrão da população $\sigma$ (ou desvio padrão da amostra se a amostra for grande).

4. Os resultados são exibidos imediatamente abaixo da calculadora.

Se você quiser encontrar $z$ com base no valor p, lembre-se de que, no caso de testes bicaudais, há dois valores possíveis de $z$: um positivo e um negativo, e eles são números opostos. Nesse caso, essa calculadora de teste Z retorna o valor positivo. Para que você encontre o outro valor possível de $z$ para um determinado valor p, basta pegar o número oposto ao valor de $z$ exibido pela calculadora.

Para ter certeza de que você entendeu completamente a essência do teste Z, vamos analisar alguns exemplos:

1. Uma máquina de enchimento de garrafas segue uma distribuição normal. Seu desvio padrão, conforme declarado pelo fabricante, é igual a 30 ml. Um vendedor de sucos afirma que o volume despejado em cada garrafa é, em média, de um litro, ou seja, 1.000 ml, mas suspeitamos que, na verdade, o volume médio seja menor do que isso...

Formalmente, as hipóteses que definimos são as seguintes:

• $\mathrm H_0 \! : \mu = 1.000 \text{ ml}$

• $\mathrm H_1 \! : \mu \lt 1.000 \text{ ml}$

Fomos a uma loja e compramos uma amostra de 9 garrafas. Depois de medir cuidadosamente o volume de suco em cada garrafa, obtivemos a seguinte amostra (em mililitros):

$\small 1.020, 970, 1.000, 980, 1.010, 930, 950, 980, 980$.

• Tamanho da amostra: $n = 9$;

• Média da amostra: $\bar x = 980 \ \mathrm{ml}$;

• Desvio padrão da população: $\sigma = 30 \ \mathrm{ml}$;

• Logo,

• E, portanto, $\text{valor p} = \Phi(-2) \approx 0,\!0228$.

  Como $0,\!0228 \lt 0,05$, concluímos que nossas suspeitas são reais; no nível de significância mais comum, 0,05, rejeitaríamos a alegação do produtor, $\mathrm H_0$, e aceitaríamos a hipótese alternativa, $\mathrm H_1$.

2. Jogamos uma moeda 50 vezes. Obtivemos 20 coroas e 30 caras. Há evidências suficientes para afirmar que a moeda é tendenciosa?

   Claramente, nossos dados seguem a distribuição de Bernoulli, com alguma probabilidade de sucesso $p$ e variância $\sigma^2 = p (1-p)$. No entanto, a amostra é grande, portanto, podemos realizar um teste Z com segurança. Adotamos a convenção de que obter a coroa é um sucesso.

   Vamos declarar as hipóteses nula e alternativa:

   • $\mathrm H_0 \! : p = 0,\!5$ (a moeda é justa: a probabilidade de coroa é $0,5$);

   • $\mathrm H_1 \! : p \ne 0,\!5$ (a moeda é tendenciosa: a probabilidade de coroa é diferente de $0,\!5$).

Em nossa amostra, temos 20 sucessos (indicados por 1) e 30 fracassos (indicados por 0), portanto:

• Tamanho da amostra $n = 50$;

• Média da amostra $\bar x = 20/50 = 0,\!4$;

• O desvio padrão da população é dado por $\sigma = \sqrt{0,\!5 \cdot 0,\!5}$ (porque $0,\!5$ é a proporção $p$ hipotetizada em $\mathrm H_0$). Portanto, $\sigma = 0,\!5$;

• Logo,

• E, portanto:

Como $0,\!1573 \gt 0,\!1$ não temos evidência suficiente para rejeitar a afirmação de que a moeda é justa, mesmo em um nível de significância tão grande como $0,\!1$. Nesse caso, você pode jogá-la com segurança ou usar a nossa calculadora de probabilidade no lançamento de moedas para descobrir suas chances de obter, por exemplo, 10 caras seguidas (que são extremamente baixas!).