Calculadora de Teste T

A calculadora de teste t da Omni te dá as boas-vindas!
Aqui você pode realizar facilmente não apenas testes t de uma única amostra, mas também testes t de duas amostras, bem como testes t pareados.

Você gostaria de encontrar o valor-p do teste t ou os valores críticos do teste t? Bem, esta calculadora de teste t pode fazer as duas coisas para você! Consulte também a [calculadora do valor-p] da Omni para mais informações sobre este valor. 😊

Mas afinal, o que é um teste t? Dê uma olhada no texto abaixo, onde explicamos o que é realmente testado quando vários tipos de testes t são realizados. Além disso, explicamos quando usar os testes t (em particular, se você deve usar o teste z ou o teste t) e quais premissas seus dados devem satisfazer para que os resultados de um teste t sejam válidos. Se você sempre quis saber como fazer um teste t manualmente, fornecemos a fórmula necessária para o teste t, além de informar como determinar o número de graus de liberdade em um teste t, no texto abaixo.

O teste t é um dos testes estatísticos mais populares para a comparação de médias, ou seja, ele lida com o(s) valor(es) médio(s) da(s) população(ões).
Existem diferentes tipos de testes t que você pode usar:

• Teste t de uma amostra;
• Teste t de duas amostras; e
• Teste t pareado.

Na próxima seção explicamos quando usar cada um deles.
Lembre-se de que o teste t só pode ser usado para um ou dois grupos. Se você precisar comparar três (ou mais) médias, use o método de análise de variância (ANOVA).

O teste t é um teste paramétrico, o que significa que seus dados devem atender a algumas premissas:

• Os dados são independentes; e
• Os dados, pelo menos aproximadamente, seguem uma distribuição normal. Consulte também a calculadora de distribuição normal da Omni para mais informação sobre este tema.

Se a sua amostra não se enquadrar nessas premissas, você pode recorrer a alternativas não paramétricas. Visite a calculadora do teste U de Mann-Whitney 🇺🇸
da Omni ou a calculadora do teste da soma dos postos de Wilcoxon 🇺🇸 para saber mais. Outras possibilidades incluem o teste dos sinais de Wilcoxon ou o teste do sinal.

A escolha do teste t depende do fato de você estar estudando um grupo ou dois grupos:

• Teste t de uma amostra

  Escolha o teste t de uma amostra para verificar se a média de uma população é igual a algum valor hipotético predefinido.

  Exemplos:

  • O volume médio de uma bebida vendida em latas de 0,33 l é realmente igual a 330 ml?
  • O peso médio das pessoas de uma cidade específica difere da média nacional?

• Teste t de duas amostras

  Escolha o teste t de duas amostras para verificar se a diferença entre as médias de duas populações é igual a algum valor predeterminado, quando as duas amostras foram escolhidas independentemente uma da outra.

  Em particular, você pode usar esse teste para verificar se os dois grupos são diferentes um do outro.

  Exemplos:

  • A diferença média no ganho de peso em dois grupos de pessoas: um grupo estava em uma dieta rica em carboidratos e o outro em uma dieta rica em gordura.
  • A diferença média nos resultados de um teste de matemática de alunos de duas universidades diferentes.

  Esse teste às vezes é chamado de teste t de amostras independentes ou teste t de amostras não pareadas.

• Teste t pareado

  Um teste t pareado é usado para investigar a mudança na média de uma população antes e depois de alguma intervenção experimental, com base em uma amostra pareada, ou seja, quando cada sujeito foi medido duas vezes: antes e depois do tratamento.

  Em particular, você pode usar esse teste para verificar se, em média, o tratamento teve algum efeito sobre a população.

  Exemplos:

  • A alteração no desempenho do aluno em um teste antes e depois de fazer um curso.
  • A alteração na pressão arterial de pacientes antes e depois da administração de algum medicamento.

Então, você decidiu qual teste t realizar. As próximas etapas mostrarão a você como calcular o valor-p do teste t ou seus valores críticos e, em seguida, qual decisão tomar sobre a hipótese nula.

1. Decida a hipótese alternativa:

   • Use um teste t bicaudal se você só se importa se a média da população (ou, no caso de duas populações, a diferença entre as médias das populações) concorda ou discorda do valor predefinido.

   • Use um teste t unicaudal se você quiser testar se essa média (ou diferença de médias) é maior ou menor que o valor predefinido.

2. Calcule o valor t:

   As fórmulas dos testes t incluem o tamanho da amostra, bem como sua média e o desvio padrão. A fórmula exata depende do tipo de teste t. Consulte as seções dedicadas a cada teste específico para obter mais detalhes.

3. Determine os graus de liberdade para o teste t:

   Os graus de liberdade são o número de observações em uma amostra livre para variar à medida que estimamos os parâmetros estatísticos. No caso mais simples, o número de graus de liberdade é igual ao tamanho da amostra menos o número de parâmetros que você precisa estimar. Novamente, a fórmula exata depende do teste t que você deseja realizar. Consulte as seções abaixo para obter mais detalhes.

Os graus de liberdade são essenciais, pois determinam a distribuição seguida pelo seu valor t (sob a hipótese nula). Se houver d graus de liberdade, a distribuição das estatísticas do teste será a distribuição t de Student com d graus de liberdade. Essa distribuição tem uma forma semelhante à N(0,1) (em forma de sino e simétrica), mas tem caudas mais pesadas. Se o número de graus de liberdade for grande (>30), o que geralmente acontece em amostras grandes, a distribuição t de Student é praticamente indistinguível da N(0,1).

Lembre-se de que o valor-p é a probabilidade (calculada sob a suposição de que a hipótese nula é verdadeira) de que o teste estatístico produzirá valores pelo menos tão extremos quanto o valor t produzido para sua amostra. Como as probabilidades correspondem a áreas sob a função de densidade, o valor-p do teste t pode ser bem ilustrado com a ajuda das figuras a seguir:

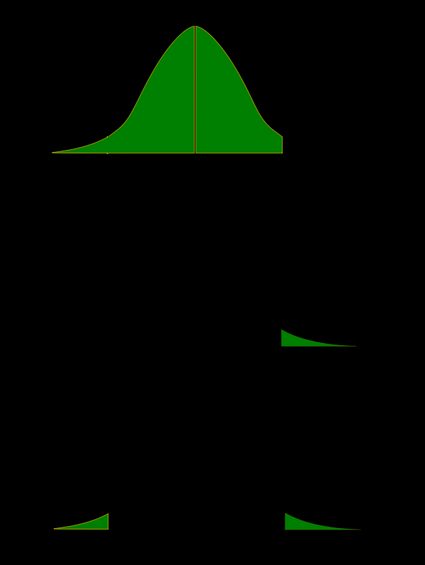
As fórmulas a seguir mostram como você pode calcular o valor-p do teste t. Por fda_t,d denotamos a função de distribuição acumulada da distribuição t de Student com d graus de liberdade:

1. Valor-p do teste t de cauda esquerda:

   valor-p = fda_t,d(valor_t)

2. Valor-p do teste t de cauda direita:

   Valor-p = 1 - fda_t,d(valor_t)

3. Valor-p do teste t de cauda dupla:

   valor-p = 2 ⋅ fda_t,d(-|valor_t|)

   ou, de forma equivalente: valor-p = 2 - 2 ⋅ fda_t,d(|valor_t|)

Entretanto, a fda da distribuição t é dado por uma fórmula um tanto complicada. Para encontrar o valor-p manualmente, você precisaria recorrer a tabelas estatísticas, onde os valores aproximados da fda são coletados, ou a um software estatístico especializado. Felizmente, nossa calculadora de teste t determina o valor-p do teste t para você em um piscar de olhos!

Lembre-se de que, na abordagem de valores críticos para o teste de hipóteses, você precisa definir um nível de significância, α, antes de calcular os valores críticos, que, por sua vez, dão origem a regiões críticas (também conhecidas como regiões de rejeição).

As fórmulas para os valores críticos empregam a função quantil da distribuição t, ou seja, o inverso da fda:

1. Valor crítico para o teste t de cauda esquerda:
   fda_t,d^-1(α)

   região crítica:

   (-∞, fda_t,d^-1(α)]

2. Valor crítico para o teste t de cauda direita:
   fda_t,d^-1(1-α)

   região crítica:

   [fda_t,d^-1(1-α), ∞)

3. Valores críticos para o teste t de dupla cauda:
   ±fda_t,d^-1(1-α/2)

   região crítica:

   (-∞, -fda_t,d^-1(1-α/2)] ∪ [fda_t,d^-1(1-α/2), ∞)

Para decidir o que acontece com a sua hipótese nula, basta verificar se o valor t está na região crítica:

• Se seu valor t pertencer à região crítica, rejeite a hipótese nula e aceite a hipótese alternativa.

• Se seu valor t estiver fora da região crítica, então você não tem evidência suficiente para rejeitar a hipótese nula.

1. Escolha o tipo de teste t que você deseja realizar:

   • Teste t de uma amostra (para testar a média de um único grupo em relação a uma média hipotética);
   • Teste t para duas amostras (para comparar as médias de dois grupos); ou
   • Teste t pareado (para verificar como a média do mesmo grupo muda após alguma intervenção).

2. Decida qual é a hipótese alternativa:

   • bicaudal;
   • de cauda esquerda; ou
   • de cauda direita.

3. Essa calculadora de teste t permite que você use tanto a abordagem do valor-p como a abordagem das regiões críticas para o teste de hipóteses!

4. Digite seu valor t e o número de graus de liberdade. Se você não os conhece, forneça alguns dados sobre sua(s) amostra(s): tamanho da amostra, média e desvio padrão, e nossa calculadora de teste t calculará o valor t e os graus de liberdade para você.

5. Quando todos os parâmetros estiverem presentes, o valor-p, ou região crítica, aparecerá imediatamente abaixo da calculadora de teste t, juntamente com uma interpretação!

1. A hipótese nula é que a média da população é igual a algum valor $\mu_0$ .

2. A hipótese alternativa é que a média da população é:

   • Diferente de $\mu_0$;
   • Menor do que $\mu_0$; ou
   • Maior que $\mu_0$.

Fórmula do teste t para uma amostra:

onde:

• $\mu_0$ é a média postulada na hipótese nula;
• $n$ é o tamanho da amostra;
• $\bar{x}$ é a média da amostra; e
• $s$ é o desvio padrão da amostra.

Número de graus de liberdade no teste t (uma amostra) = $n-1$.

1. A hipótese nula é que a diferença real entre as médias desses grupos, $\mu_1$ e $\mu_2$, é igual a algum valor predefinido, $\Delta$.

2. A hipótese alternativa é que a diferença $\mu_1 - \mu_2$ é:

   • Diferente de $\Delta$;
   • Menor do que $\Delta$; ou
   • Maior do que $\Delta$.

Em particular, se essa diferença predeterminada for zero ($\Delta = 0$):

1. A hipótese nula é que as médias da população são iguais.

2. A hipótese alternativa é que as médias da população são:

   • $\mu_1$ e $\mu_2$ são diferentes uma da outra;
   • $\mu_1$ é menor do que $\mu_2$; e
   • $\mu_1$ é maior do que $\mu_2$.

Formalmente, para realizar um teste t, devemos supor adicionalmente que as variâncias das duas populações são iguais (essa suposição é chamada de homogeneidade de variância).

Há uma versão do teste t que pode ser aplicada sem a suposição de homogeneidade da variância: é chamada de teste t de Welch. Para sua conveniência, descrevemos as duas versões.

Teste t de duas amostras se as variâncias forem iguais

Use este teste se você souber que as variâncias das duas populações são iguais (ou muito semelhantes).

Fórmula do teste t para duas amostras (com variâncias iguais):

onde $s_p$ é o chamado desvio padrão agrupado, que calculamos como:

onde

• $\Delta$ é a diferença média postulada na hipótese nula;
• $n_1$ é o tamanho da primeira amostra;
• $\bar{x}_1$ é a média da primeira amostra;
• $s_1$ é o desvio padrão na primeira amostra;
• $n_2$ é o tamanho da segunda amostra;
• $\bar{x}_2$ é a média da segunda amostra; e
• $s_2$ é o desvio padrão na segunda amostra.

Número de graus de liberdade no teste t (duas amostras, variâncias iguais) = $n_1 + n_2 - 2$.

Teste t de duas amostras se as variâncias forem desiguais (teste t de Welch)

Use este teste se as variâncias de suas populações forem diferentes.

Fórmula do teste t de Welch para duas amostras se as variâncias forem desiguais:

onde:

• $\Delta$ é a diferença média postulada na hipótese nula;
• $n_1$ é o tamanho da primeira amostra;
• $\bar{x}_1$ é a média da primeira amostra;
• $s_1$ é o desvio padrão na primeira amostra;
• $n_2$ é o tamanho da segunda amostra;
• $\bar{x}_2$ é a média da segunda amostra; e
• $s_2$ é o desvio padrão na segunda amostra.

O número de graus de liberdade em um teste t de Welch (teste t para duas amostras com variâncias desiguais) é muito difícil de contar. Podemos aproximá-lo com a ajuda da seguinte fórmula de Satterthwaite:

Como alternativa, você pode considerar o menor de $n_1 - 1$ e $n_2 - 1$ como uma estimativa conservadora do número de graus de liberdade.

Como geralmente realizamos um teste t pareado quando temos dados sobre os mesmos indivíduos medidos duas vezes (antes e depois de algum tratamento), vamos adotar a convenção de nos referirmos às amostras como grupo antes e grupo depois.

1. A hipótese nula é que a verdadeira diferença entre as médias das populações antes e depois é igual a algum valor predefinido, $\Delta$.

2. A hipótese alternativa é que a diferença real entre essas médias é:

   • Diferente de $\Delta$;
   • Menor do que $\Delta$; ou
   • Maior do que $\Delta$.

Normalmente, essa diferença predeterminada é zero. Podemos então reformular as hipóteses da seguinte forma:

1. A hipótese nula é que as médias antes e depois são as mesmas, ou seja, o tratamento não tem impacto sobre a população.

2. A hipótese alternativa:

   • As médias antes e depois são diferentes uma da outra (o tratamento tem algum efeito);
   • A média antes é menor que a média depois (o tratamento aumenta o resultado); ou
   • A média antes é maior do que a média depois (o tratamento diminui o resultado).

Fórmula do teste t pareado

Na verdade, um teste t pareado é tecnicamente o mesmo que um teste t de uma amostra! Vejamos por que isso acontece. Suponhamos que $x_1, ... , x_n$ são as observações feitas antes e $y_1, ... , y_n$ são as observações feitas depois do tratamento. Ou seja, $x_i, y_i$ são as medições feitas antes e depois do tratamento do i-ésimo sujeito.

Para cada sujeito, calcule a diferença, $d_i := x_i - y_i$. Tudo o que acontece a seguir é apenas um teste t de uma amostra realizado na amostra de diferenças $d_1, ... , d_n$. Dê uma olhada na fórmula do valor t:

onde:

• $\Delta$ é a diferença média postulada na hipótese nula;

• $n$ é o tamanho da amostra de diferenças, ou seja, o número de pares;

• $\bar{x}$ é a média da amostra de diferenças; e

• $s$ é o desvio padrão da amostra de diferenças.

Número de graus de liberdade no teste t (pareado): $n - 1$

Usamos um teste z quando queremos testar a média populacional de um conjunto de dados normalmente distribuído, com uma variância populacional conhecida. Se o número de graus de liberdade for grande, a distribuição t de Student será muito próxima de N(0,1).

Portanto, se houver muitos dados na amostra (pelo menos 30), você pode trocar um teste t por um teste z, e os resultados serão quase idênticos. Entretanto, para amostras pequenas com variância desconhecida, lembre-se de usar o teste t porque, nesse caso, a distribuição t de Student difere significativamente da N(0,1)!