Calculadora de Distribuição Normal

A calculadora de distribuição normal da Omni (também chamada de calculadora de curva de sino) calcula a área sob uma curva de sino e estabelece a probabilidade de um valor ser maior ou menor do que qualquer valor arbitrário X. Você também pode usar esta calculadora de distribuição de probabilidade para encontrar a probabilidade de sua variável estar em qualquer intervalo arbitrário, de X a X₂, apenas usando os valores média de distribuição normal e desvio padrão. Este artigo explica alguns termos básicos sobre a distribuição normal padrão, fornece a você a fórmula da Função de Distribuição Acumulada normal (FDA normal) e fornece exemplos da distribuição de probabilidade normal.

A distribuição normal (também conhecida como Gaussiana) é uma distribuição de probabilidade contínua. A maioria dos dados está próximo de um valor central, sem tendência para a esquerda ou para a direita. Muitas observações na natureza, como a altura das pessoas ou a pressão arterial, seguem essa distribuição.

Em uma distribuição normal, o valor da média também é a mediana (o número “médio” de uma lista ordenada de dados) e a moda (o valor com a maior frequência de ocorrência). Como essa distribuição é simétrica em relação ao centro, 50% dos valores são menores que a média e 50% dos valores são maiores que a média.

Outro parâmetro que caracteriza a distribuição normal é o desvio padrão 🇺🇸. Ele descreve o quanto os números estão espalhados. Geralmente, 68% dos valores devem estar dentro de 1 desvio padrão da média, 95% dentro de 2 desvios padrão e 99,7% dentro de 3 desvios padrão. O número de desvios padrão da média é chamado de escore padrão (aprenda mais na calculadora de escore padrão Z da Omni). Pode ser que você conheça a variância, mas não o desvio padrão da sua distribuição. No entanto, é fácil para você calculá-lo simplesmente pegando a raiz quadrada da variância.

Podemos dizer que um aumento no valor médio desloca toda a curva em forma de sino para a direita. Se você alterar o desvio padrão, a distribuição em torno da média se torna mais estreita ou dispersa. Em distribuições fortemente dispersas, há uma probabilidade maior de um ponto de dados aleatório cair longe da média. A forma da curva de sino é determinada apenas por esses dois parâmetros.

Você pode padronizar qualquer distribuição normal, o que é feito por um processo conhecido como pontuação padrão. Isso ocorre quando você subtrai a média da população da pontuação dos dados e divide essa diferença pelo desvio padrão da população. Uma distribuição normal padrão tem as seguintes propriedades:

• O valor médio é igual a 0;
• O desvio padrão é igual a 1;
• A área total sob a curva é igual a 1; e
• Cada valor da variável x é convertido no escore padrão correspondente.

Você pode verificar essa ferramenta usando também a calculadora de distribuição normal padrão. Se você entrar com a média, μ, como 0 e o desvio padrão, σ, como 1, o escore padrão será igual a X.

A área total sob a curva de distribuição normal padrão é igual a 1, o que significa que ela corresponde a probabilidade. Você pode calcular a probabilidade de que seu valor seja menor do que qualquer X arbitrário (denotado como P(x < X)) como a área sob o gráfico à esquerda do escore padrão de X.

Vamos dar uma olhada novamente no gráfico acima e considerar os valores da distribuição dentro de um desvio padrão. Você pode ver que a probabilidade restante (0,32) consiste em duas regiões. A cauda direita e a cauda esquerda da distribuição normal são simétricas, cada uma com uma área de 0,16. Essa beleza matemática é exatamente o motivo pelo qual os cientistas de dados adoram a distribuição gaussiana!

O cálculo da área sob o gráfico não é uma tarefa fácil. Você pode usar a tabela de distribuição normal ou tentar integrar a função de distribuição acumulada normal (FDA normal):

Por exemplo, suponha que você queira encontrar a probabilidade de uma variável ser menor que $x$. Nesse caso, você deve integrar essa função de menos infinito a $x$. Da mesma forma, se quiser encontrar a probabilidade de a variável ser maior que $x$, você deve integrar essa função de $x$ a infinito. Certifique-se de conferir a calculadora de valor-p para obter mais informações sobre esse tópico.

Você também pode usar esta calculadora como uma calculadora de FDA normal!

Observe, no entanto, que a função de distribuição acumulada da distribuição normal não deve ser confundida com sua função de densidade (a curva de sino), que simplesmente atribui o valor de probabilidade a todos os argumentos:

Por definição, a função de densidade é a primeira derivada, ou seja, a taxa de alteração da FDA normal.

1. Decida a média de sua distribuição normal. Por exemplo, podemos tentar analisar a distribuição de altura numa determinada população. A altura média de um homem adulto é de 175,7 cm.

2. Escolha o desvio padrão para seu conjunto de dados. Digamos que ele seja igual a 10 cm.

3. Digamos que você queira usar essa calculadora de curva de sino para determinar a probabilidade de um adulto ter mais de 185 cm de altura. Então, seu $X$ será igual a 185 cm.

4. Nossa calculadora de distribuição normal exibirá dois valores: a probabilidade de uma pessoa ser mais alta que 185 cm ($P(x > X)$) e mais baixa que 185 cm ($P(x < X)$). Nesse caso, a primeira é igual a 17,62% e a segunda é igual a 82,38%.

5. Você também pode abrir o Modo avançado da calculadora para calcular a probabilidade de uma variável $x$ estar em um intervalo específico (de X a X₂). Por exemplo, a probabilidade de que a altura de um homem americano adulto esteja entre 185 e 190 cm é igual a 9,98%.

A distribuição normal descreve muitos fenômenos naturais: processos que acontecem continuamente e em grande escala. De acordo com a lei dos grandes números, o valor médio de um tamanho de amostra suficientemente grande, quando desenhado a partir de alguma distribuição, estará próximo da média de sua distribuição subjacente (se quiser saber mais, consulte a calculadora de tamanho de amostra 🇺🇸 da Omni). Quanto mais medições você pegar, mais se aproximará do valor real da média para a população.

No entanto, lembre-se de que uma das tendências estatísticas mais robustas é a regressão em direção à média. Cunhado por um famoso cientista britânico, Francis Galton, esse termo nos lembra que as coisas tendem a se igualar com o tempo. Os pais mais altos tendem a ter, em média, filhos com altura mais próxima da média. Após um período de alto crescimento do PIB (Produto Interno Bruto), um país tende a passar por alguns anos de produção total mais moderada.

Com frequência, pode acontecer que a variação natural, em dados repetidos, se pareça muito com uma mudança real. No entanto, é simplesmente um fato estatístico que observações relativamente altas (ou baixas) são frequentemente seguidas por outras com valores mais próximos da média. A regressão à média costuma ser a fonte de evidências anedóticas que não podemos confirmar por motivos estatísticos.

A distribuição normal é conhecida por suas probabilidades matemáticas. Várias probabilidades, tanto discretas quanto contínuas, tendem a convergir para a distribuição normal. Isso é chamado de teorema do limite central e é claramente um dos teoremas mais importantes da estatística. Graças a ele, você pode usar a calculadora de média de distribuição normal e desvio padrão para simular a distribuição até mesmo dos conjuntos de dados mais complexos.

À medida que o tamanho da amostra fica cada vez maior, o valor médio se aproxima da normalidade, independentemente da forma inicial da distribuição da população. Por exemplo, com um número suficientemente grande de observações, a distribuição normal pode ser usada para aproximar a distribuição de Poisson ou a distribuição de probabilidade binomial. Consequentemente, muitas vezes consideramos a distribuição normal como a distribuição limitante de uma sequência de variáveis aleatórias.

É por isso que a prática recomendada diz que muitos testes e procedimentos estatísticos precisam de uma amostra de mais de 30 pontos de dados para garantir que você obtenha uma distribuição normal. Na linguagem estatística, essas propriedades são frequentemente chamadas de assintóticas.

Se você não tiver certeza de qual é a distribuição subjacente dos seus dados, mas puder obter um grande número de observações, pode ter certeza de que eles seguem a distribuição normal. Isso é verdadeiro até mesmo para os fenômenos aleatórios, ou seja, processos que evoluem sem nenhum padrão ou tendência discernível.

Uma tabela de distribuição normal padrão, como a que está abaixo, é um ótimo lugar para você verificar os valores referenciais ao construir intervalos de confiança. Você pode usar nossa calculadora de probabilidade de distribuição normal para confirmar se o valor que você usou para construir os intervalos de confiança está correto. Por exemplo, se X = 1,96, então X é o ponto de percentil 97,5 da distribuição normal padrão. Não se esqueça de defina a média = 0, o desvio padrão = 1 e X = 1,96; observe que 97,5% dos valores estão abaixo de X.

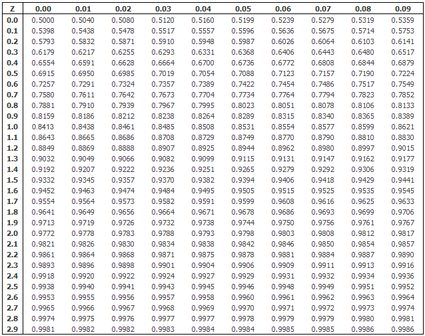
Além disso, desde que a observação usada seja aleatória e independente, a média da população e os valores de variância estimados a partir da amostra também são independentes. A distribuição gaussiana univariada (calculada para uma única variável) também pode ser generalizada para um conjunto de variáveis. Uma “soma” específica chamada distribuição normal multivariada mostra a distribuição conjunta de um número específico de variáveis. Você pode usá-la para modelar dados de dimensões mais altas, como uma avaliação abrangente de pacientes.

Os estatísticos baseiam muitos tipos de testes estatísticos na suposição de que as observações usadas no procedimento de teste seguem a distribuição gaussiana. Ela é válida para quase todas as estatísticas inferenciais quando você usa as informações da amostra para fazer generalizações sobre toda a população.

Por exemplo, você pode verificar formalmente se o valor estimado de um parâmetro é estatisticamente diferente de zero ou se um valor médio em uma população é igual ao da outra. A maioria dos testes simples que ajudam você a responder a essas perguntas (os chamados testes paramétricos) depende da hipótese nula. Você não pode usá-la quando uma distribuição empírica tem propriedades diferentes das de uma distribuição normal.

Você deve testar essa suposição antes de aplicar esses testes. Existem alguns testes populares de normalidade para determinar se a distribuição de dados é normal. O teste de Shapiro-Wilk baseia sua análise na variância da amostra. Por outro lado, o teste de Jarque-Bera é baseado em distorção e excesso de curtose da distribuição empírica. Em ambos os testes, você pode fazer uma interpretação precisa e manter o poder explicativo dos modelos estatísticos.

O teste de normalidade também te ajuda a verificar se você pode esperar taxas de retorno excessivas sobre ativos financeiros, como ações, ou o desempenho de sua carteira em relação ao mercado. Podemos usar a média da distribuição empírica para aproximar a eficácia do seu investimento. Por outro lado, você pode usar a variância para avaliar o risco que caracteriza um portfólio.

Uma das suposições de normalidade mais comumente usadas diz respeito a modelos de regressão lineares (ou mesmo não lineares). Normalmente, supomos que os resíduos do estimador de mínimos quadrados seguem uma distribuição normal com um valor médio de zero e um desvio padrão fixo (invariante no tempo) (você pode pensar nesses resíduos como a distância entre uma reta de regressão e os pontos de dados reais). Você pode avaliar a adequação do modelo de mínimos quadrados usando o teste do qui-quadrado. No entanto, se a distribuição de erros não for normal, isso pode significar que suas estimativas são tendenciosas ou ineficazes.

Outro exemplo importante nessa área é a ANOVA (análise de variância), usada para verificar se os valores médios de duas amostras são iguais. A ANOVA também pode ser usada com sucesso na forma canônica quando a distribuição dos resíduos do modelo é normal.

Há várias maneiras pelas quais a distribuição dos seus dados pode se desviar da distribuição da curva de sino, mas as duas mais importantes são:

• Caudas gordas: valores extremos podem ocorrer com probabilidades mais altas (por exemplo, há uma chance relativamente alta de obter resultados anormais);
• Assimétricas: a distribuição é assimétrica. Os valores médios e medianos da distribuição são diferentes (por exemplo, dispersão de salários no mercado de trabalho).

As distribuições não normais são comuns em finanças, mas você pode esperar que os mesmos tipos de problemas apareçam em psicologia ou estudos sociais. Um dos muitos exemplos de tais distribuições é a distribuição geométrica, adequada para modelar vários eventos independentes, por exemplo, o resultado de lançar dados.

A distribuição normal (ou distribuição gaussiana) é uma distribuição de probabilidade em forma de sino para variáveis aleatórias independentes. Ela é crucial para a estatística porque descreve com precisão a distribuição de valores de muitos fenômenos naturais. A curva de distribuição é simétrica em torno de sua média, com a maioria das observações agrupadas em torno de um pico central e as probabilidades diminuindo para valores mais distantes da média em qualquer direção.

Sim, uma distribuição normal pode ter um grande desvio padrão em comparação com a média. Por exemplo, uma distribuição normal pode ter uma média de 6, mas um desvio padrão de 20. Em geral, quanto mais larga for a distribuição normal em relação à média, maior será seu desvio padrão.

Para determinar se um conjunto de dados é normalmente distribuído, você pode usar o método de análise de dados:

1. Desenhe um gráfico da distribuição de dados.
2. Verifique se a curva tem a forma de um sino simétrico centrado em torno da média.
3. Verifique a regra empírica: 68% dos valores devem estar dentro de 1 desvio padrão da média, 95% dentro de 2 desvios padrão e 99,7% dentro de 3 desvios padrão.

Os dois principais parâmetros da distribuição normal são: média (μ) e desvio padrão (σ). O parâmetro μ determina a localização do pico da distribuição normal no eixo numérico. σ é um parâmetro de escala que faz com que a distribuição normal se propague mais em valores maiores do que σ.

2,5%, supondo que, para um carvalho, a distribuição normal da circunferência tenha μ = 150 cm e σ = 30 cm.

1. Desenhe a distribuição normal com o pico em μ = 150 cm e σ = 30 cm.
2. Observe que a circunferência de 210 cm está 2σ = 60 cm acima da média.
3. Use a regra empírica de que 95% dos dados estão dentro de ±2σ.
4. Divida por 2 para pegar as árvores com circunferência acima de +2σ.