Calculadora de Valor-p

Esta é a calculadora de valor-p da Omni! Com essa ferramente, você não precisará mais se perguntar como encontrar o valor-p, pois aqui você pode determinar os valor-p unilateral e bilateral de testes estatísticos, seguindo as distribuições mais populares: normal, t-Student, qui-quadrado e F de Snedecor.

O valor-p é comum em toda a ciência, mas muitas pessoas acham o seu conceito um pouco difícil. Mas, aqui você não precisa se preocupar! Neste artigo, explicaremos não apenas o que é o valor-p, mas também como interpretá-lo corretamente. Você já teve curiosidade de saber como calcular o valor-p manualmente? Também fornecemos a você todas as fórmulas necessárias!

Formalmente, o valor-p é a probabilidade de que o teste estatístico produza valores pelo menos tão extremos quanto o valor que ela produziu para sua amostra. É fundamental lembrar que essa probabilidade é calculada sob a suposição de que a hipótese nula H₀ seja verdadeira!

De forma mais intuitiva, o valor-p responde à pergunta:

Supondo que eu viva em um mundo em que a hipótese nula seja verdadeira, qual é a probabilidade de que, para outra amostra, o teste que estou realizando gere um valor pelo menos tão extremo quanto o que observei para a amostra que já tenho?

É a hipótese alternativa que determina o que "extremo" realmente significa, portanto, o valor-p depende da hipótese alternativa que você declara: de cauda esquerda, de cauda direita ou bicaudal. Nas fórmulas abaixo, S representa um teste estatístico, x o valor que ele produziu para uma determinada amostra e Pr(evento | H₀) é a probabilidade de um evento, calculada sob a suposição de que H₀ é verdadeira:

1. Teste de cauda esquerda: valor-p = Pr(S ≤ x | H₀)

2. Teste de cauda direita: valor-p = Pr(S ≥ x | H₀)

3. Teste bicaudal:

   valor-p = 2 × min{Pr(S ≤ x | H₀), Pr(S ≥ x | H₀)}

   (Por min{a,b}, denotamos o menor número entre a e b)

   Se a distribuição da estatística de teste em H₀ for simétrica em relação a 0, então:
   valor-p = 2 × Pr(S ≥ |x| | H₀)

   ou, de forma equivalente:
   valor-p = 2 × Pr(S ≤ -|x| | H₀)

Como uma imagem vale mais que mil palavras, vamos ilustrar essas definições. Aqui, usamos que a probabilidade pode ser perfeitamente representada como a área sob a curva de densidade de uma determinada distribuição. Apresentamos dois conjuntos de imagens: um para uma distribuição simétrica e outro para uma distribuição enviesada (não simétrica).

• Caso simétrico: distribuição normal:

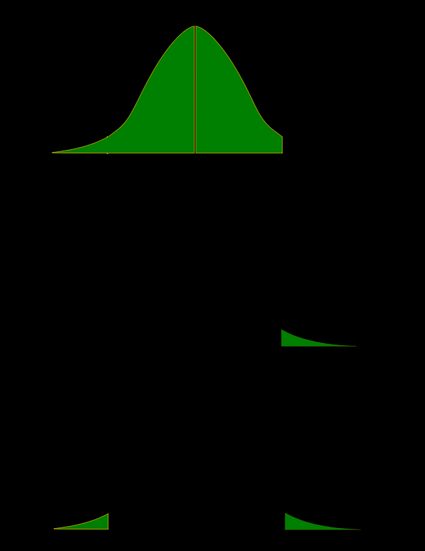
• Caso não simétrico: distribuição qui-quadrado:

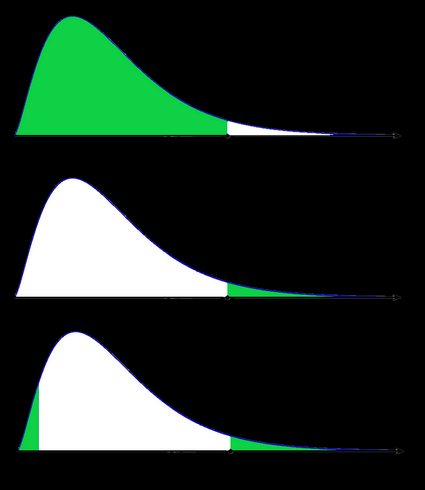
Na última figura (valor-p bicaudal para distribuição não simétrica), a área do lado esquerdo é igual à área do lado direito.

Para determinar o valor-p, você precisa conhecer a distribuição do seu teste estatístico sob a suposição de que a hipótese nula seja verdadeira. Em seguida, com a ajuda da Função de Distribuição Acumulada (FDA) dessa distribuição, podemos expressar a probabilidade do teste estatístico ser pelo menos tão extremo quanto seu valor x para a amostra:

1. Teste de cauda esquerda:

   valor-p = fda(x).

2. Teste de cauda direita:

   valor-p = 1 - fda(x).

3. Teste bicaudal:

   valor-p = 2 × min{fda(x) , 1 - fda(x)}.

   Se a distribuição do teste estatístico em H₀ for simétrica em relação a 0, então um valor-p bicaudal pode ser simplificado para valor-p = 2 × fda(-|x|) ou, de forma equivalente, como valor-p = 2 - 2 × fda(|x|).

As distribuições de probabilidade mais comuns nos testes de hipóteses tendem a ter fórmulas de FDA complicadas, e talvez não seja possível encontrar o valor-p manualmente. Você provavelmente precisará recorrer a um computador ou a uma tabela estatística, que contém os valores aproximados de FDA.

Agora você já sabe como calcular o valor-p, mas, por que você precisa calculá-lo em primeiro lugar? No teste de hipóteses, a abordagem do valor-p é uma alternativa à abordagem do valor crítico. Lembre-se de que a última exige que os pesquisadores pré-definam o nível de significância, α, que é a probabilidade de rejeitar a hipótese nula quando ela é verdadeira (portanto, erro tipo I). Após obter o valor-p, você só precisa compará-lo com um determinado α para decidir rapidamente se deve ou não rejeitar a hipótese nula nesse nível de significância, α. Para obter detalhes, consulte a próxima seção, onde explicamos como interpretar os valores p.

Como mencionamos acima, o valor-p é a resposta para a seguinte pergunta:

Supondo que eu viva em um mundo em que a hipótese nula seja válida, qual é a probabilidade de que, para outra amostra, o teste que estou realizando gere um valor pelo menos tão extremo quanto o que observei para a amostra que já tenho?

O que isso significa para você? Bem, você tem duas opções:

• Um valor-p alto significa que seus dados são altamente compatíveis com a hipótese nula; e
• Um valor-p baixo fornece evidência contra a hipótese nula, pois significa que seu resultado seria muito improvável se a hipótese nula fosse verdadeira.

Entretanto, pode acontecer de a hipótese nula ser verdadeira, mas sua amostra ser altamente incomum! Por exemplo, imagine que estudamos o efeito de um novo medicamento e obtivemos um valor-p de 0,03. Isso significa que em 3% de estudos semelhantes, o acaso sozinho ainda seria capaz de produzir o valor do teste estatístico que obtivemos, ou um valor ainda mais extremo, mesmo que o medicamento não tivesse efeito algum!

A pergunta "o que é valor-p" também pode ser respondida da seguinte forma: valor-p é o menor nível de significância no qual a hipótese nula seria rejeitada. Portanto, se você quiser tomar uma decisão sobre a hipótese nula em algum nível de significância α, basta comparar seu valor-p com α:

• Se valor-p ≤ α, então você rejeita a hipótese nula e aceita a hipótese alternativa; e
• Se valor-p ≥ α, então você não tem evidência suficiente para rejeitar a hipótese nula.

Obviamente, o destino da hipótese nula depende de α. Por exemplo, se o valor-p fosse 0,03, rejeitaríamos a hipótese nula em um nível de significância de 0,05, mas não em um nível de 0,01. É por isso que o nível de significância deve ser declarado com antecedência e não adaptado convenientemente após o valor-p ter sido estabelecido! Um nível de significância de 0,05 é o valor mais comum, mas não há nada de mágico nele. Aqui, você pode encontrar o porquê um nível de significância de 0,05 é confiável. No entanto, é sempre melhor informar o valor-p e permitir que o leitor tire suas próprias conclusões.

Além disso, lembre-se de que a experiência no assunto (e o bom senso) são fundamentais para interpretar os resultados de um teste estatístico. Caso contrário, aplicando princípios estatísticos sem pensar, você pode facilmente chegar a um resultado estatisticamente significativo, apesar de a conclusão ser 100% falsa.

Como a nossa calculadora de valor-p está aqui à sua disposição, você não precisa mais se perguntar como encontrar o valor-p de todas aquelas testes estatísticos complicados! Aqui estão as etapas que você precisa seguir:

1. Escolha a hipótese alternativa: bicaudal, de cauda direita ou de cauda esquerda.

2. Diga-nos qual é a distribuição do teste estatístico sob a hipótese nula: é N(0,1), t-Student, qui-quadrado ou F de Snedecor? Se você não tiver certeza, consulte as seções abaixo, pois elas são dedicadas a essas distribuições.

3. Se necessário, especifique os graus de liberdade da distribuição do teste estatístico.

4. Digite o valor do teste estatístico calculado para sua amostra de dados.

5. Nossa calculadora determina o valor-p do teste estatístico e fornece a decisão a ser tomada sobre a hipótese nula. O nível de significância que a calculadora utiliza é, por padrão, 0,05.

Vá para o modo avançado se você precisar aumentar a precisão com a qual os cálculos são realizados, ou seja, alterar o nível de significância.

Em termos da Função de Distribuição Acumulada (FDA) da distribuição normal padrão, que é tradicionalmente denotada por Φ, é possível encontrar o valor-p a partir do escore padrão (valor-z) da seguinte forma:

1. Teste z de cauda esquerda:

   valor-p = Φ(valor-z)

2. Teste z de cauda direita:

   valor-p = 1 - Φ(valor-z)

3. Teste z bicaudal:

   valor-p = 2 × Φ(-|valor-z|)

   ou

   valor-p = 2 - 2 × Φ(|valor-z|)

Usamos o escore padrão ou escore-z se o teste estatístico seguir aproximadamente a distribuição normal padrão N(0,1). Graças ao teorema do limite central, você pode contar com a aproximação se tiver uma amostra grande (digamos, pelo menos 50 dados) e tratar sua distribuição como normal.

Um teste z geralmente se refere ao teste da média da população ou à diferença entre duas médias da população, em particular entre duas proporções. Você também pode encontrar testes z em estimativas de máxima verossimilhança.

O valor-p do valor-t é dado pelas seguintes fórmulas, nas quais fda_t,d representa a função de distribuição acumulada da distribuição t de Student com d graus de liberdade:

1. Teste t de cauda esquerda:

   valor-p = fda_t,d(valor-t)

2. Teste t de cauda direita:

   valor-p = 1 - fda_t,d(valor-t)

3. Teste t bicaudal:

   valor-p = 2 × fda_t,d(-|valor-t|)

   ou

   valor-p = 2 - 2 × fda_t,d(|valor-t|)

Use a opção do valor-t se o teste estatístico seguir a distribuição t de Student. Essa distribuição tem uma forma semelhante à N(0,1) (em forma de sino e simétrica), mas tem caudas mais pesadas. A forma exata depende do parâmetro chamado graus de liberdade. Se o número de graus de liberdade for grande (>30), o que geralmente ocorre em amostras grandes, a distribuição t de Student é praticamente indistinguível da distribuição normal N(0,1).

Os testes t mais comuns são aqueles para médias populacionais com um desvio padrão populacional desconhecido ou para a diferença entre médias de duas populações, com desvios padrões populacionais iguais ou desiguais, porém desconhecidos. Há também um teste t para amostras pareadas (dependentes).

Use a opção do valor-χ² ao realizar um teste no qual o teste estatístico segue a distribuição χ².

Essa distribuição surge se, por exemplo, você pegar a soma de variáveis quadradas, cada uma seguindo a distribuição normal N(0,1). Lembre-se de verificar o número de graus de liberdade da distribuição χ² do seu teste!

Como encontrar o valor-p da distribuição qui-quadrado? Você pode fazer isso com a ajuda das seguintes fórmulas, nas quais fda_χ²,d denota a função de distribuição acumulada da distribuição χ² com d graus de liberdade:

1. Teste de χ² de cauda esquerda:

   valor-p = fda_χ²,d(valor-χ²)

2. Teste do χ² de cauda direita:

   valor-p = 1 - fda_χ²,d(valor-χ²)

   Lembre-se de que os testes de χ² para adequação e independência são testes de cauda direita! (veja abaixo)

3. Teste χ² bicaudal:

   valor-p = 2 × min{fda_χ²,d(valor-χ²), 1 - fda_χ²,d(valor-χ²)}

   (Por min{a,b}, denotamos o menor dos números a e b)

Os testes mais populares que levam a um escore χ² são os seguintes:

• Testar se a variância de dados normalmente distribuídos tem algum valor predeterminado. Nesse caso, o teste estatístico tem a distribuição χ² com n - 1 graus de liberdade, em que n é o tamanho da amostra. Esse pode ser um teste unicaudal ou bicaudal.

• O teste de bondade de ajuste verifica se a distribuição empírica (da amostra) está de acordo com alguma distribuição de probabilidade esperada. Nesse caso, o teste estatístico segue a distribuição χ² com k - 1 graus de liberdade, em que k é o número de classes em que a amostra está dividida. Esse é um teste de cauda direita.

• o teste de independência é usado para determinar se há uma relação estatisticamente significativa entre duas variáveis. Nesse caso, seu teste estatístico baseia-se na tabela de contingência e segue a distribuição χ² com (r - 1)(c - 1) graus de liberdade, em que r é o número de linhas e c é o número de colunas nessa tabela de contingência. Esse também é um teste de cauda direita.

Por fim, a opção do valor-F deve ser usada quando você realiza um teste no qual o teste estatístico segue a distribuição F, também conhecida como distribuição Fisher-Snedecor. A forma exata de uma distribuição F depende de dois graus de liberdade.

Para ver de onde vêm esses graus de liberdade, considere as variáveis aleatórias independentes X e Y, que seguem as distribuições χ² com d₁ e d₂ graus de liberdade, respectivamente. Nesse caso, a razão (X/d₁)/(Y/d₂) segue a distribuição F, com (d₁, d₂) graus de liberdade. Por esse motivo, os dois parâmetros d₁ e d₂ também são chamados de graus de liberdade do numerador e do denominador.

O valor-p do valor-F é dado pelas fórmulas a seguir, em que fda_F,d1,d2 denota a função de distribuição acumulada da distribuição F, com (d₁, d₂) graus de liberdade:

1. Teste F de cauda esquerda:

   valor-p = fda_F,d1,d2(valor-F)

2. Teste F de cauda direita:

   valor-p = 1 - fda_F,d1,d2(valor-F)

3. Teste F bicaudal:

   valor-p = 2 × min{fda_F,d1,d2(valor-F), 1 - fda_F,d1,d2(valor-F)}

   (Por min{a,b}, denotamos o menor dos números a e b)

Abaixo, listamos os testes mais importantes que seguem a distribuição F. Todos eles são testes de cauda direita.

• Um teste para a igualdade de variâncias em duas populações normalmente distribuídas. Seu teste estatístico segue a distribuição F com (n - 1, m - 1) graus de liberdade, em que n e m são os respectivos tamanhos de amostra.

• a ANOVA é usada para testar a igualdade de médias em três ou mais grupos provenientes de populações normalmente distribuídas com variâncias iguais. Chegamos à distribuição F com (k - 1, n - k) graus de liberdade, em que k é o número de grupos e n é o tamanho total da amostra (em todos os grupos juntos).

• Um teste para significância geral da análise de regressão. O teste estatístico tem uma distribuição F com (k - 1, n - k) graus de liberdade, em que n é o tamanho da amostra e k é o número de variáveis (incluindo a interceptação).

  Com a presença da relação linear estabelecida em sua amostra de dados com o teste acima, você pode calcular o coeficiente de determinação, R², que indica a força dessa relação. Você pode fazer isso manualmente ou usar a calculadora do coeficiente de determinação (R²) 🇺🇸 da Omni.

• Um teste para comparar dois modelos de regressão aninhados. O teste estatístico segue a distribuição F com (k₂ - k₁, n - k₂) graus de liberdade, em que k₁ e k₂ são os números de variáveis nos modelos menor e maior, respectivamente, e n é o tamanho da amostra.

  Você pode notar que o teste F de uma significância geral é uma forma particular do teste F para comparar dois modelos agrupados: ele testa se o nosso modelo é significativamente melhor do que o modelo sem preditores (ou seja, o modelo somente de interceptação).

Não, o valor-p não pode ser negativo. Isso ocorre porque as probabilidades não podem ser negativas, e o valor-p é a probabilidade da estatística de teste atender a determinadas condições.

Um valor-p alto significa que, sob a hipótese nula, há uma grande probabilidade de que, para outra amostra, o teste estatístico gere um valor pelo menos tão extremo quanto o observado na amostra que você já tem. Um valor-p alto não permite que você rejeite a hipótese nula.

Um valor-p baixo significa que, sob a hipótese nula, há pouca probabilidade de que, para outra amostra, o teste estatístico gere um valor pelo menos tão extremo quanto o observado para a amostra que você já tem. Um valor-p baixo é uma evidência a favor da hipótese alternativa, ou seja, ele permite que você rejeite a hipótese nula.