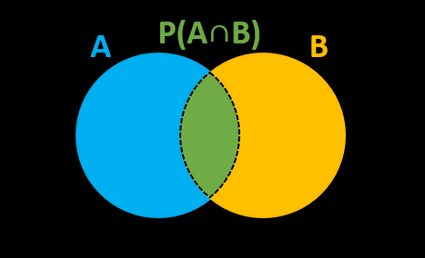
Calculadora de Probabilidade

Com a calculadora de probabilidade, você pode investigar as relações de probabilidade entre dois eventos distintos. Por exemplo, se a chance de A acontecer é de 50%, qual a chance de B ocorrer? Quais são as chances de ambos ocorrerem? De apenas um, de pelo menos um, ou ainda, de nenhum ocorrer e assim por diante.

Nossa calculadora de probabilidade fornece seis cenários, além de mais 4 quando você insere quantas vezes o "dado é lançado", por assim dizer. Desde que você saiba como encontrar a probabilidade de eventos individuais, isso lhe poupará muito tempo.

Lendo o texto a seguir, você vai:

• O que é probabilidade;
• Descobrir como usar corretamente a calculadora de probabilidade;
• Verificar como encontrar a probabilidade de eventos individuais;
• Entender o conceito de distribuição de probabilidade;
• Ler sobre vários exemplos de uso de probabilidade, incluindo fórmulas de probabilidade condicional;
• Estudar a diferença entre uma probabilidade teórica e empírica; e
• Aumentar seu conhecimento sobre a relação entre probabilidade e estatística e sobre amostragem probabilística.

Você veio aqui especificamente para verificar suas chances de ganhar uma aposta ou tirar a sorte grande? Nossa calculadora de probabilidades e calculadora de loteria 🇺🇸 ajudarão você!

Se você quer saber a resposta para a pergunta "o que é probabilidade?", veio ao lugar certo. A probabilidade pode ser definida como a proporção de todos os resultados favoráveis em relação ao número de todos os resultados possíveis.

Os valores permitidos de uma única probabilidade variam de 0 a 1, portanto, também é conveniente escrever as probabilidades como porcentagens. A probabilidade de um único evento pode ser expressa dessa forma:

• A probabilidade de A: P(A),
• A probabilidade de B: P(B),
• A probabilidade de +: P(+),
• A probabilidade de ♥: P(♥), etc.

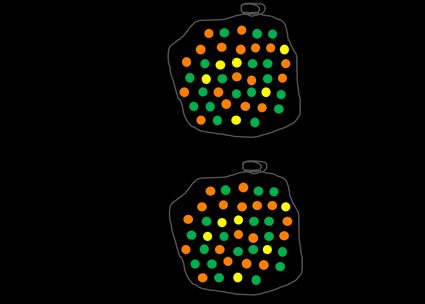
Vamos fazer o cálculo de probabilidade a partir de um exemplo com bolas multicoloridas. Temos um saco cheio de bolas laranjas, verdes e amarelas. Nosso evento A consiste em escolher uma bola aleatória do saco. Podemos definir Ω como um conjunto completo de bolas. A probabilidade do evento Ω, que significa escolher qualquer bola, é naturalmente 1. Na verdade, a soma de todos os eventos possíveis em um determinado conjunto é sempre igual a 1.

Agora vamos analisar algo mais desafiador: qual é a probabilidade de você escolher uma bola laranja? Para responder a essa pergunta, você precisa encontrar o número de todas as bolas laranja e dividi-lo pelo número de todas as bolas no saco. Você pode fazer isso para qualquer cor, por exemplo, amarelo, e, sem dúvida, perceberá que quanto mais bolas de uma determinada cor, maior a probabilidade de retirá-la do saco, se o processo for totalmente aleatório.

Cada um dos eventos do exemplo do saco com bolas coloridas forma nosso conjunto ou espaço de dados, também conhecido como espaço amostral, sendo este um conceito fundamental em estatística. Os eventos de um espaço amostral são chamados tecnicamente de pontos amostrais.

Confira a calculadora da probabilidade de 3 eventos e a calculadora de probabilidade condicional 🇺🇸 da Omni, para determinar as chances de vários eventos.

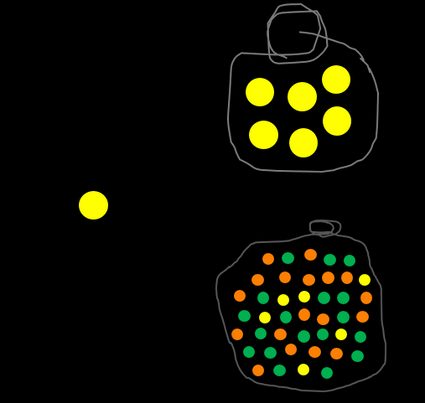
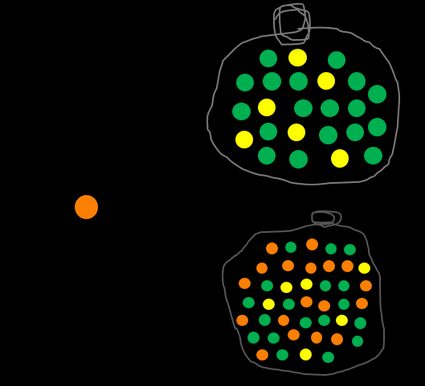
Podemos definir um evento complementar, escrito como Ā ou A', que significa não A. Em nosso exemplo, a probabilidade de você NÃO escolher uma bola laranja é avaliada como o número de todas as bolas não laranjas dividido por todas as bolas do saco. A soma P(A) + P(Ā) é sempre 1 porque não há outra opção, como metade de uma bola ou uma bola meio laranja.

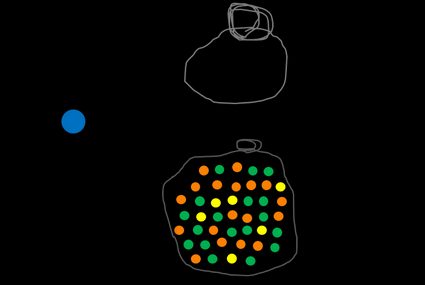
Agora, tente descobrir a probabilidade de você obter uma bola azul. Não importa o quanto tente, você não conseguirá, pois não há uma sequer no saco, portanto o resultado é igual a 0.

Usamos cálculos intuitivos de probabilidade o tempo todo. Saber como quantificar a probabilidade é essencial para a análise estatística. Isso permite que você meça esse conceito, muitas vezes tão temido, chamado "probabilidade". Além disso, dado um conjunto de dados discreto, a frequência relativa de cada valor é sinônimo da probabilidade de sua ocorrência. Se interessa por esse assunto? Confira a calculadora de frequência relativa da Omni.

Você está procurando algo um pouco diferente? Dê uma olhada na calculadora de probabilidade pós-teste 🇺🇸 da Omni. 🎲

Para aproveitar ao máximo a nossa calculadora, você precisará seguir as seguintes etapas:

1. Defina o problema que você deseja resolver

Seu problema precisa ser dividido em dois eventos independentes.

2. Encontre a probabilidade de cada evento

Agora que você sabe como estimar a probabilidade de um único evento, só precisa executar a tarefa e obter todos os valores necessários.

3. Digite a probabilidade percentual de cada evento nos campos correspondentes

Depois de inseridos, a calculadora de probabilidade será imediatamente preenchida com a probabilidade exata de 6 cenários diferentes:

• Ambos A e B acontecem;
• Pelo menos um dos eventos acontece;
• Exatamente um dos eventos acontece;
• Nenhum dos eventos acontece;
• Apenas o primeiro evento não acontece; e
• Apenas o segundo evento não acontece.

A calculadora também mostrará a probabilidade de mais quatro cenários, considerando um determinado número de tentativas:

• A sempre acontece;
• A nunca acontece;
• B sempre acontece; e
• B nunca acontece.

Você pode alterar o número de tentativas e qualquer outro campo da calculadora, e os outros campos se ajustarão automaticamente. Esse recurso economiza muito tempo se você quiser descobrir, por exemplo, qual seria a probabilidade do evento "B" para que a probabilidade de ambos ocorrerem seja de 50%.

Se o conjunto de escolhas possíveis for extremamente grande e apenas alguns resultados forem bem-sucedidos, a probabilidade resultante será pequena, como P(A) = 0,0001. É conveniente usar a notação científica para que você não confunda o número de zeros.

Uma das considerações mais importantes no mundo das probabilidades é se os eventos são dependentes ou não. Dois eventos são independentes se a ocorrência do primeiro não afetar a probabilidade de ocorrência do segundo. Por exemplo, se lançarmos um dado cúbico padrão perfeitamente equilibrado, a possibilidade de obter um dois ⚁ é igual a 1/6 (o mesmo que obter um quatro ⚃ ou qualquer outro número).

Vamos considerar um exemplo envolvendo dados. Digamos que você faça dois lançamentos e obtenha um cinco ⚄ no primeiro. Se você se perguntar qual é a probabilidade de obter um dois ⚁ na segunda jogada, a resposta será 1/6 mais uma vez devido à independência dos eventos.

A maneira de pensar, assim como os cálculos, mudam se um dos eventos interromper todo o sistema. Desta vez, estamos falando de probabilidade condicional.

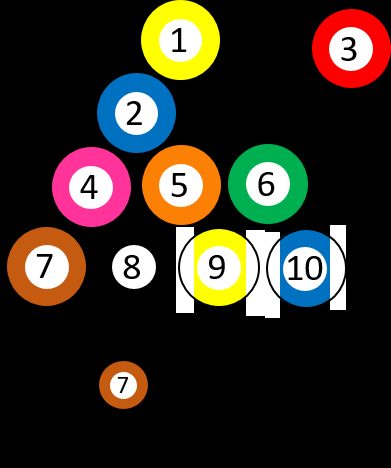
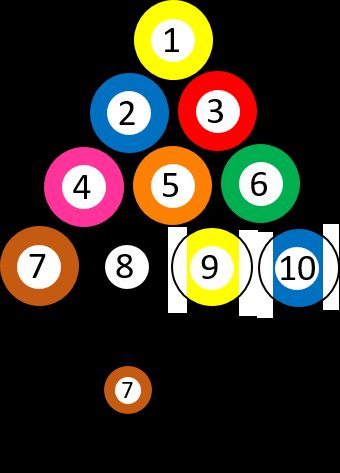
Digamos que você tenha 10 bolas de bilhar numeradas diferentes, de ➀ a ➉. Você escolhe uma bola aleatória, de modo que a probabilidade de obter a ➆ é precisamente 1/10. Suponha que você tenha pego a bola três ➂ e retirado-a do jogo. Então você se pergunta, mais uma vez, qual é a chance de obter o sete ➆. A situação mudou porque há uma bola com ➆ entre nove possibilidades, o que significa que a probabilidade agora é 1/9. Em outras palavras, você pode fazer a pergunta: "Qual é a probabilidade de você escolher ➆, SE a primeira bola for ➂?"

Vejamos outro exemplo: imagine que você vai fazer uma prova de estatística. Você sabe, por meio de seus colegas mais velhos, que é um desafio e que a probabilidade de você ser aprovado no primeiro período é de 0,5 (18 dos 36 alunos foram aprovados no ano passado). Então, vamos fazer uma pergunta a você mesmo: "Qual é a probabilidade de passar se você já estudou o assunto?" 20 pessoas admitiram ter revisado suas anotações pelo menos uma vez antes do exame, e 16 delas foram aprovadas, o que significa que a resposta à última pergunta é 0,8. Esse resultado indica que essa condição adicional é realmente importante se quisermos descobrir se estudar melhora o seu desempenho ou não

Se você ainda não entendeu o conceito de probabilidade condicional, vamos tentar com outro exemplo: você precisa ir da cidade X para a cidade Y de carro. A distância entre elas é de cerca de 150 km. Com o tanque cheio, você geralmente pode percorrer até 400 km. Se você não souber o nível de combustível, poderá estimar a probabilidade de chegar ao destino sem reabastecer. E se alguém já tiver enchido o tanque? Agora você tem quase certeza de que conseguirá chegar ao destino, a menos que outros problemas o impeçam.

A expressão formal da probabilidade condicional, que pode ser denotada como P(A|B), P(A/B) ou P_B(A), é calculada da seguinte forma:

P(A|B) = P(A∩B) / P(B),

em que P(B) é a probabilidade de um evento B e P(A∩B) é a probabilidade conjunta de ambos os eventos. Por outro lado, podemos estimar a interseção de dois eventos se soubermos uma das probabilidades condicionais:

• P(A∩B) = P(A|B) · P(B) ou
• P(A∩B) = P(B|A) · P(A).

É mais fácil entender o conceito de fórmula de probabilidade condicional com diagramas de árvore. Suponhamos que, em uma aula, perguntamos aos alunos se eles gostam de matemática e física. Um evento "M" indica a porcentagem de quem gosta de matemática (math) e "P" de quem gosta de física (physics):

Há um teorema famoso que conecta as probabilidades condicionais de dois eventos. Ele se chama Teorema de Bayes, e a fórmula é a seguinte:

P(A|B) = P(B|A) · P(A) / P(B)

Você pode se perguntar: "Qual é a probabilidade de A dado B se eu souber a probabilidade de B dado A?". Esse teorema às vezes fornece resultados surpreendentes e não muito intuitivos. Os exemplos mais comumente descritos são os testes de drogas e a detecção de doenças, que têm muito em comum com o risco relativo de doenças na população. Por hora, vamos nos ater ao segundo exemplo. Em um grupo de 1000 pessoas, 10 delas têm uma doença rara. Todos fizeram um teste, que mostra o resultado real em 95% dos casos. Portanto, agora queremos descobrir a probabilidade de uma pessoa estar doente se o resultado do teste for positivo.

Sem pensar, você pode prever, por intuição, que o resultado deve ser em torno de 90%, certo? Vamos fazer alguns cálculos e estimar a resposta correta.

1. Usaremos uma notação: S para saudável, D para doente, + para teste positivo, - para teste negativo.
2. Reescreva as informações do texto acima em uma forma de probabilidades: P(S) = 0,99, P(D) = 0,01, P(+|D) = 0,95, P(-|D) = 0,05, P(+|S) = 0,05, P(-|S) = 0,95.
3. Calcule a probabilidade total de um teste ser positivo: P(+) = P(+|D) · P(D) + P(+|S) · P(S) = 0,95 · 0,01 + 0,05 · 0,99 = 0,059.
4. Use o teorema de Bayes para encontrar a probabilidade condicional P(D|+) = P(+|D) · P(D) / P(+) = 0,95 · 0,01 / 0,059 = 0,161.

Hmm... o resultado não foi tão alto quanto você previu, certo? Acontece que esse tipo de paradoxo ocorre quando há um desequilíbrio significativo entre o número de pessoas saudáveis e doentes ou, em geral, entre dois grupos distintos. Se o resultado for positivo, sempre vale a pena repetir o teste para fazer um diagnóstico adequado.

Podemos distinguir entre dois tipos de distribuições de probabilidade, dependendo se as variáveis aleatórias são discretas ou contínuas.

• Uma distribuição de probabilidade discreta descreve a probabilidade da ocorrência de eventos distintos e contáveis. Um dos exemplos é a probabilidade binomial, que leva em conta a probabilidade de algum tipo de sucesso em várias jogadas. Por outro lado, na distribuição de Pascal (também conhecida como binomial negativa), o número fixo de sucessos é dado e você deseja estimar o número total de tentativas.

  A distribuição de Poisson é outra distribuição de probabilidade discreta e é, na verdade, um caso particular da binomial, que você pode calcular com a calculadora de distribuição de Poisson 🇺🇸 da Omni. A função massa de probabilidade pode ser interpretada como outra definição de distribuição de probabilidade discreta. Ela atribui um determinado valor a qualquer número separado. A calculadora de distribuição geométrica 🇺🇸, também da Omni, mostra alguns exemplos de uso da função massa de probabilidade.

• Uma distribuição de probabilidade contínua contém informações sobre eventos incontáveis. É impossível prever a probabilidade de um único evento (como em uma distribuição discreta). Contudo, podemos encontrar o evento em algum intervalo de variáveis. A distribuição normal é uma das funções de distribuição contínua mais conhecidas. Ela descreve uma série de propriedades em qualquer população, por exemplo, a altura de pessoas adultas ou a distribuição de QI. A função que descreve a probabilidade de ver dois resultados em um determinado intervalo de valores é chamada de função de densidade de probabilidade.

Se você for mais avançado em teoria e no cálculo de probabilidade, certamente poderá lidar com a calculadora de distribuições de probabilidade 🇺🇸, que leva em conta a combinação de várias funções de probabilidade discretas e contínuas.

Para cada distribuição de probabilidade, podemos construir a função de distribuição acumulada (FDA). Ela informa a você qual é a probabilidade de alguma variável tomar o valor menor ou igual a um determinado número.

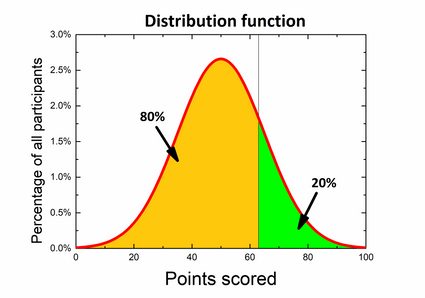
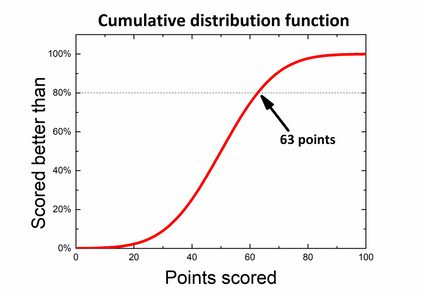
Digamos que você participe de um teste de conhecimentos gerais. A competição consiste em 100 perguntas, e você ganha 1 ponto pela resposta correta, enquanto não há pontos pela resposta errada. Muitas pessoas já terminaram e, a partir dos resultados, podemos obter uma distribuição de probabilidade. As regras estabelecem que apenas 20% dos melhores participantes recebem prêmios, então você se pergunta qual deve ser a sua pontuação para ser um dos vencedores. Se você observar o gráfico, poderá dividi-lo de forma que 80% da área abaixo esteja no lado esquerdo e 20% dos resultados estejam à direita da pontuação desejada. Na verdade, o que você está procurando é um valor-p de cauda esquerda.

No entanto, também há outra maneira de encontrá-lo, usando uma função de distribuição acumulada. Para isso, basta encontrar o valor 80% no eixo das abscissas e o número de pontos correspondente sem calcular nada!

Quase todos os exemplos descritos acima levam em conta a probabilidade teórica. Portanto, surge uma pergunta: qual é a diferença entre a probabilidade teórica e a experimental (também conhecida como empírica)? A definição de probabilidade teórica estabelece que: a probabilidade teórica é a razão entre o número de resultados favoráveis e o número de todos os resultados possíveis. Ela se baseia nas informações fornecidas, no raciocínio lógico e nos diz o que devemos esperar de um experimento.

Basta olhar novamente para o saco com bolas coloridas. Há 42 bolas no total, e 18 delas são laranjas. O jogo consiste em pegar uma bola aleatória do saco e colocá-la de volta, de modo que sempre há 42 bolas dentro dele. Aplicando a definição de probabilidade, podemos estimá-la rapidamente como 18/42, ou simplificando a fração, 3/7. Isso significa que, se pegarmos 14 bolas, deverá haver 6 bolas laranjas.

Por outro lado, a probabilidade experimental nos diz exatamente o que aconteceu quando realizamos um experimento em vez do que deveria acontecer. Ela se baseia na razão entre o número de tentativas bem-sucedidas e o número de todas as tentativas. Vamos continuar com o mesmo exemplo. Escolha uma bola de gude aleatória do saco e repita o procedimento 13 vezes. Suponha que você obtenha 8 bolas laranjas em 14 tentativas. Esse resultado significa que a probabilidade empírica é 8/14 ou 4/7.

Como você pode ver, seu resultado é diferente do teórico. Isso não é estranho, pois quando você tenta repetir esse jogo várias vezes, às vezes, você escolhe mais, às vezes, menos e, às vezes, escolhe exatamente o número previsto teoricamente. Se você somar todos os resultados, deverá notar que a probabilidade geral fica cada vez mais próxima da probabilidade teórica. Caso contrário, podemos suspeitar que a escolha de uma bola do saco não é totalmente aleatória, por exemplo, as bolas de cores diferentes têm tamanhos desiguais, de modo que você pode distingui-las sem precisar olhar.

Tanto a estatística quanto a probabilidade são os ramos da matemática que lidam com a relação da ocorrência de eventos. Entretanto, todos devem estar cientes das diferenças que as tornam duas áreas distintas.

• A probabilidade é geralmente um campo teórico da matemática e investiga as consequências das definições e teoremas matemáticos. Por outro lado, a estatística é geralmente uma aplicação prática da matemática em situações cotidianas e tenta atribuir sentido e compreensão às observações no mundo real.

• A probabilidade prevê a possibilidade de ocorrência de eventos, enquanto a estatística serve basicamente para analisar a frequência de ocorrência de eventos passados e criar um modelo com base no conhecimento adquirido.

• Imagine um probabilista jogando um jogo de cartas, que depende da escolha de uma carta aleatória de todo o baralho, sabendo que apenas espadas vencem com uma proporção de chances predefinida. Supondo que o baralho esteja completo e que a escolha seja totalmente aleatória e equitativa, eles deduzem que a probabilidade é igual a ¼ e podem fazer uma aposta.

• Um estatístico observará o jogo por um tempo primeiro para verificar se, de fato, o jogo é justo. Após verificar (com uma aproximação aceitável) que vale a pena jogar, ele perguntará ao probabilista o que ele deve fazer para ganhar mais.

Sem dúvida, você já viu algumas pesquisas de preferência eleitoral e deve ter se perguntado como elas podem ser tão precisas em comparação com as pontuações finais, mesmo que o número de pessoas entrevistadas seja muito menor do que a população total. Isso se trata de amostragem probabilística.

O pressuposto subjacente, que é a ideia básica da amostragem, é que os voluntários são escolhidos aleatoriamente com uma probabilidade previamente definida. Você pode distinguir entre vários tipos de métodos de amostragem probabilística:

• Amostragem aleatória simples
• Amostragem aleatória de grupos
• Amostragem sistemática
• Amostragem proporcional ao tamanho da probabilidade
• Amostragem aleatória estratificada
• Amostragem minimax
• Amostragem acidental
• Amostragem por cotas
• Amostragem voluntária
• Amostragem de painel
• Amostragem de bola de neve
• Amostragem por interceptação de linha
• Amostragem teórica

Cada um desses métodos tem suas vantagens e desvantagens, mas a maioria deles é satisfatório. Os benefícios significativos da amostragem probabilística são a economia de tempo e a relação custo-benefício, já que um número limitado de pessoas precisa ser pesquisado. A simplicidade desse procedimento não requer nenhum conhecimento especializado e pode ser realizado sem nenhuma preparação completa.

Como você já deve ter percebido, há muitos cenários onde o cálculo de probabilidade é aplicável. A maioria deles são jogos com um alto fator aleatório, como, por exemplo, escolher uma bola colorida entre 10 cores diferentes, ou muitos jogos de cartas. As loterias e os jogos de azar são os tipos de jogos que usam amplamente o conceito de probabilidade e a falta geral de conhecimento sobre ele. É claro que alguém ganha de vez em quando, mas a probabilidade de que essa pessoa seja você é extremamente pequena.

A teoria da probabilidade também é usada em muitos tipos diferentes de problemas. Especialmente quando se trata de investimentos, também vale a pena considerar o risco para escolher a opção mais adequada.

Está pensando em passar o natal em um lugar que neva e prever se realmente você vai ver um lugar cheio de neve? A calculadora de neve no natal 🇺🇸 da Omni usa dados históricos e conhecimento de probabilidade para prever a ocorrência de cobertura de neve em muitas cidades durante o Natal.