Kalkulator wartości krytycznej

Witamy w Omni kalkulatorze wartości krytycznej! Tutaj możesz szybko wyznaczyć wartości krytyczne dla testów dwustronnych jak i dla testów jednostronnych. Nasze narzędzie obsługuje rozkłady często spotykane w testach statystycznych: nie tylko rozkład normalny N(0,1) (czyli posługujący się wartością Z), ale też t-Studenta, chi-kwadrat i rozkład F.

Co to jest wartość krytyczna? Jaki jest wzór na wartość krytyczną? W dalszej części tekstu podamy ci definicję wartości krytycznej i wyjaśnimy, jak ją obliczyć, by móc następnie użyć jej do wyznaczania zbiorów krytycznych.

W testowaniu hipotez statystycznych wyznaczenie wartości krytycznych to jedna z dwóch możliwych strategii, które pozwalają zdecydować o przyjęciu bądź odrzuceniu hipotezy zerowej. Drugim podejściem jest obliczenie tzw. wartości p (ang. p-value, więcej dowiesz się w Omni kalkulatorze wartości p).

Metoda wartości krytycznej polega na sprawdzeniu, czy wartość statystyki testowej wygenerowana przez próbkę należy do tak zwanego zbioru krytycznego, który jest obszarem wartości, które statystyka testowa przyjmuje z bardzo małym prawdopodobieństwem. Wartość krytyczna to wartość (lub dwie wartości w przypadku testu dwustronnego), która stanowi brzeg zbioru krytycznego. Innymi słowy, wartości krytyczne wyodrębniają zbiór krytyczny w zbiorze wartości statystyki testowej.

Po znalezieniu zbioru krytycznego sprawdź, czy wartość statystyki testowej wygenerowanej przez twoją próbkę do niego należy:

• Jeśli tak, to odrzucasz hipotezę zerową i przyjmujesz hipotezę alternatywną.
• Jeśli nie, to nie masz wystarczających przesłanek, aby odrzucić H₀.

Jak zatem obliczyć wartości krytyczne? Przede wszystkim należy ustalić poziom istotności, $\alpha$, który określa dopuszczalne prawdopodobieństwo błędnego odrzucenia hipotezy zerowej, czyli gdy jest ona w rzeczywistości prawdziwa. Wybór $\alpha$ jest dowolny; w praktyce najczęściej używamy wartości 0,05 lub 0,01. Wartości krytyczne zależą również od hipotezy alternatywnej wybranej dla testu, co wyjaśnimy szerzej w następnej sekcji.

Aby znaleźć wartości krytyczne, należy znać rozkład statystyki testowej przy założeniu, że hipoteza zerowa jest prawdziwa. Wartości krytyczne to punkty o następującej własności: prawdopodobieństwo, że twoja statystyka testowa przyjmie wartości co najmniej tak skrajne, jak te punkty, jest równe poziomowi istotności $\alpha$. Hm, trochę skomplikowana definicja. Nie martw się, wszystko wyjaśnimy.

Po pierwsze: to hipoteza alternatywna określa, co należy rozumieć przez „skrajne”. W szczególności, jeśli test jest jednostronny, to będzie tylko jedna wartość krytyczna; jeśli jest dwustronny, to będą dwie: jedna po lewej, a druga po prawej stronie mediany rozkładu.

Wartości krytyczne można też rozumieć jako punkty o tej własności, że obszar pod krzywą gęstości statystyki testowej pomiędzy tymi punktami a ogonami rozkładu jest równy $\alpha$:

• Test lewostronny: obszar pod krzywą gęstości od wartości krytycznej w lewo jest równy $\alpha$.

• Test prawostronny: obszar pod krzywą gęstości od wartości krytycznej w prawo jest równy $\alpha$.

• Test dwustronny: obszar pod krzywą gęstości od lewej wartości krytycznej w lewo jest równy $\alpha/2$, a obszar pod krzywą od prawej wartości krytycznej w prawo jest również równy $\alpha/2$; zatem całkowity obszar jest ponownie równy $\alpha$.

Jak widzimy, znalezienie wartości krytycznych dla testu dwustronnego z poziomem istotności $\alpha$ sprowadza się do znalezienia dwóch jednostronnych wartości krytycznych z poziomem istotności $\alpha/2$.

Wzory na wartości krytyczne obejmują funkcję kwantylową, $Q$, która jest odwrotnością dystrybuanty ($\mathrm{cdf}$) rozkładu statystyki testowej (obliczonej przy założeniu, że H₀ jest prawdziwa): $Q = \mathrm{cdf}^{-1}$.

Po ustaleniu poziomu istotności $\alpha$, wzory na wartości i zbiory krytyczne są następujące:

1. Test lewostronny:

2. Test prawostronny:

3. Test dwustronny:

W przypadku rozkładu symetrycznego względem 0, wartości krytyczne dla testu dwustronnego są również symetryczne:

Rozkłady prawdopodobieństwa, które są najbardziej rozpowszechnione w testowaniu hipotez, mają niestety dość skomplikowane wzory na dystrybuantę $\mathrm{cdf}$. Aby ręcznie znaleźć wartości krytyczne, należałoby użyć tablic statystycznych lub specjalistycznego oprogramowania, jak na przykład Omni kalkulator wartości krytycznej! 😁

Gdy już znasz nasz kalkulator wartości krytycznej, nie musisz się martwić szukaniem wartości krytycznych dla tych wszystkich skomplikowanych rozkładów! Wystarczy, że wykonasz następujące kroki:

1. Podaj nam rozkład statystyki testowej przy hipotezie zerowej: czy jest to standardowy rozkład normalny N(0,1), t-Studenta, chi-kwadrat, czy F Snedecora? Jeśli nie masz pewności, sprawdź dalsze sekcje, które poświęcamy poszczególnym rozkładom, i spróbuj znaleźć w nich test, który chcesz wykonać.

2. Wybierz hipotezę alternatywną: dwustronną, prawostronną lub lewostronną.

3. W razie potrzeby określ liczbę stopni swobody rozkładu twojej statystyki testowej. Jeśli nie jesteś jej pewien, sprawdź definicję wykonywanego testu. O stopniach swobody dowiesz się więcej z Omni kalkulatora stopni swobody.

4. Ustal poziom istotności, $\alpha$. Domyślnie ustawiliśmy go na najbardziej powszechną wartość 0,05, ale możesz oczywiście dostosować go do swoich potrzeb.

5. Kalkulator wartości krytycznych poda ci nie tylko wartości krytyczne, ale także zbiory krytyczne.

Wybierz tryb zaawansowany (advanced mode) naszego kalkulatora wartości krytycznych, jeśli chcesz zwiększyć precyzję, z jaką prowadzone są obliczenia.

Użyj w kalkulatorze opcji Z (standardowy normalny) jeśli twoja statystyka testowa ma (przynajmniej w przybliżeniu) standardowy rozkład normalny N(0,1).

W poniższych wzorach $u$ oznacza funkcję kwantylową standardowego rozkładu normalnego N(0,1):

1. Lewostronna wartość krytyczna Z: $u(\alpha)$

2. Prawostronna wartość krytyczna Z: $u(1-\alpha)$

3. Dwustronna wartość krytyczna Z: $\pm u(1-\alpha/2)$

Odwiedź nasz kalkulator testu Z, aby dowiedzieć się więcej o teście Z dla średniej w populacji. Istnieją również testy Z dla różnicy między dwiema średnimi populacji, w szczególności między dla różnicy dwiema proporcjami.

Użyj opcji t-Student, jeśli twoja statystyka testowa ma rozkład t-Studenta. Rozkład ten jest podobny do N(0,1), ale jego ogony są cięższe — dokładny kształt rozkładu zależy od liczby stopni swobody. Jeśli liczba ta jest duża (>30), co zwykle ma miejsce w przypadku dużych próbek, wówczas rozkład t-Studenta jest praktycznie nieodróżnialny od N(0,1). Sprawdź nasz kalkulator statystyki t, aby obliczyć odpowiednią statystykę testową.

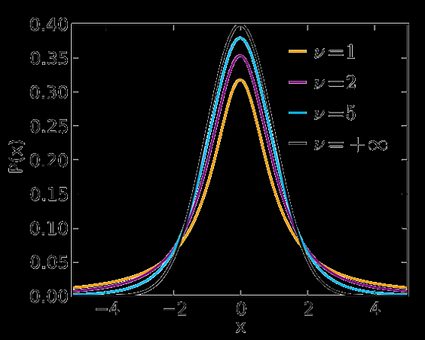
W poniższych wzorach $Q_{\text{t}, d}$ oznacza funkcję kwantylową rozkładu t-Studenta o $d$ stopniach swobody:

1. Lewostronna wartość krytyczna t: $Q_{\text{t}, d}(\alpha)$

2. Prawostronna wartość krytyczna t: $Q_{\text{t}, d}(1 - \alpha)$

3. Dwustronne wartości krytyczne t: $\pm Q_{\text{t}, d}(1 - \alpha/2)$

Odwiedź kalkulator testu t, aby dowiedzieć się więcej o różnych typach testu t: dla średniej populacji o nieznanym odchyleniu standardowym, dla różnicy między średnimi dwóch populacji (z równymi lub różnymi lecz nieznanymi odchyleniami standardowymi), a także o teście t dla próbek sparowanych.

Użyj w kalkulatorze opcji χ² (chi-kwadrat) jeśli przeprowadzasz test, w którym statystyka testowa ma rozkład χ².

Musisz określić liczbę stopni swobody rozkładu statystyki testowej — poniżej podamy je dla najczęściej używanych testów χ².

Oto wzory na wartości krytyczne rozkładu chi-kwadrat; $Q_{\chi^2,d}$ jest funkcją kwantylową rozkładu χ² o $d$ stopniach swobody:

1. Lewostronna wartość krytyczna χ²: $Q_{\chi^2, d}(\alpha)$

2. Prawostronna wartość krytyczna χ²: $Q_{\chi^2, d}(1 - \alpha)$

3. Dwustronne wartości krytyczne χ²: $Q_{\chi^2, d}(\alpha/2)$ i $Q_{\chi^2, d}(1 - \alpha/2)$

Istnieje kilka różnych testów, które mogą doprowadzić cię do rozkładu χ²:

• Test zgodności rozkładów: czy rozkład empiryczny zgadza się z rozkładem oczekiwanym?

  Ten test jest prawostronny. Jego statystyka testowa ma rozkład χ² z $k - 1$ stopniami swobody, gdzie $k$ to liczba klas, na które podzielona jest próba.

• Test niezależności: czy istnieje statystycznie istotny związek między dwiema zmiennymi?

  Ten test jest również prawostronny, a jego statystyka testowa jest obliczana na podstawie tabeli krzyżowej. Mamy wtedy $(r - 1)(c - 1)$ stopni swobody, gdzie $r$ to liczba wierszy, a $c$ to liczba kolumn w tabeli krzyżowej.

• Test na wariancję danych o rozkładzie normalnym: czy ta wariancja ma jakąś z góry określoną wartość?

  Ten test może być jedno- lub dwustronny, w zależności od hipotezy alternatywnej. Jego statystyka testowa ma rozkład χ² z $n - 1$ stopniami swobody, gdzie $n$ to wielkość próby.

Wybierz w kalkulatorze opcję F (Fisher-Snedecor), jeśli statystyka testowa ma rozkład F. Rozkład ten ma parę stopni swobody $(d_1, d_2)$.

Skąd biorą się te stopnie swobody? Załóżmy, że mamy dwie niezależne zmienne losowe, $X$ i $Y$, które mają rozkład χ² o stopniach swobody odpowiednio $d_1$ i $d_2$. Wówczas iloraz $(\frac{X}{d_1}):(\frac{Y}{d_2})$ będzie miał rozkład F ze stopniami swobody $(d_1, d_2)$. Z tego powodu $d_1$ i $d_2$ są czasami nazywane odpowiednio licznikiem i mianownikiem stopni swobody.

W poniższych wzorach $Q_{\text{F}, d_1, d_2}$ oznacza funkcję kwantylową rozkładu F ze stopniami swobody $(d_1, d_2)$:

1. Lewostronna wartość krytyczna F: $Q_{\text{F}, d_1, d_2}(\alpha)$

2. Prawostronna wartość krytyczna F: $Q_{\text{F}, d_1, d_2}(1 - \alpha)$

3. Dwustronne wartości krytyczne F: $Q_{\text{F}, d_1, d_2}(\alpha/2)$ i $Q_{\text{F}, d_1, d_2}(1 - \alpha/2)$

Wymieńmy najważniejsze testy, które prowadzą do rozkładu F. Co istotne, każdy z nich jest prawostronny.

• ANOVA: testuje równość średnich w trzech lub więcej grupach. W każdej grupie dane pochodzą z populacji o rozkładzie normalnym i wariancje tych rozkładów są równe. Mamy tu $(k - 1, n - k)$ stopni swobody, gdzie $k$ to liczba grup, a $n$ to całkowita wielkość próby (w każdej grupie).

• Istotność modelu regresji liniowej. Statystyka testowa ma $(k - 1, n - k)$ stopni swobody, gdzie $n$ to liczebność próby, a $k$ to liczba zmiennych (łącznie z wyrazem wolnym).

• Porównanie dwóch zagnieżdżonych modeli regresji. Statystyka testowa ma rozkład F o $(k_2 - k_1, n - k_2)$ stopniach swobody, gdzie $k_1$ i $k_2$ to liczba zmiennych odpowiednio w mniejszym i większym modelu, a $n$ to wielkość próby.

• Równość wariancji w dwóch populacjach o rozkładzie normalnym. Mamy wówczas $(n - 1, m - 1)$ stopni swobody, gdzie $n$ i $m$ są wielkościami badanych próbek.

Wartość krytyczna Z to wartość, która definiuje zbiór krytyczny w testowaniu hipotez, gdy statystyka testowa ma standardowy rozkład normalny. Jeśli wartość statystyki testowej znajduje się w zbiorze krytycznym, należy odrzucić hipotezę zerową i przyjąć hipotezę alternatywną.

Aby znaleźć wartość krytyczną Z dla danego poziomu ufności α:

1. Sprawdź, czy wykonujesz test jedno- czy dwustronny.
2. Dla testu jednostronnego:
   • Lewostronny: wartością krytyczną jest kwantyl rzędu α standardowego rozkładu normalnego N(0,1).
   • Prawostronny: wartością krytyczną jest kwantyl rzędu (1-α) rozkładu N(0,1).
3. Test dwustronny: wartości krytyczne to kwantyle rzędu ±(1-α/2) rozkładu N(0,1).
4. Nie masz tablic statystycznych? Użyj tablic dystrybuanty! (Funkcja kwantylowa jest odwrotnością dystrybuanty.)
5. Możesz sprawdzić swój wynik w Omni kalkulatorze wartości krytycznych.

W teorii, nie. W praktyce, bardzo często, tak. Rozkład t-Studenta jest podobny do standardowego rozkładu normalnego, ale nie jest identyczny. Jeśli jednak liczba stopni swobody (czyli, z grubsza rzecz biorąc, wielkość próby) jest wystarczająco duża (>30), wówczas oba rozkłady są praktycznie nierozróżnialne, a zatem wartość krytyczna t ma praktycznie taką samą wartość jak wartość krytyczna Z.

Wartość krytyczna Z dla 95% przedziału ufności wynosi:

• 1,96 dla testu dwustronnego,
• 1,64 dla testu prawostronnego,
• -1,64 dla testu lewostronnego.