Kalkulator testu t Studenta

Witamy w naszym kalkulatorze testu t! Tutaj możesz nie tylko łatwo wykonać testy t z jedną próbką, ale także testy t z dwiema próbkami, a także testy t.

Czy wolisz znaleźć wartość p z testu t, czy raczej wartości krytyczne testu t? Ten kalkulator testu t może zrobić jedno i drugie! 😊

Co mówi ci test t? Zapoznaj się z poniższym tekstem, w którym wyjaśniamy, co faktycznie jest testowane podczas wykonywania różnych typów testów t. Wyjaśniamy również, kiedy należy stosować testy t (w szczególności, czy należy użyć testu z czy testu t) i jakie założenia powinny spełniać Twoje dane, aby wyniki testu t były ważne. Jeśli kiedykolwiek chciałeś wiedzieć, jak wykonać test t ręcznie, podajemy niezbędną formułę testu t, a także mówimy, jak określić liczbę stopni swobody w teście t.

Więcej informacji na temat różnych parametrów statystycznych znajdziesz również w naszym artykule: wartość p a wartość t.

Test t-Studenta jest jednym z najpopularniejszych testów statystycznych dla lokalizacji, dotyczących średnich wartości populacji. Jest to technika statystyczna do pomiaru różnicy między średnimi wartościami jednego i dwóch zbiorów danych próbki poprzez rozważenie testowania hipotez. Jest również znany jako test t-Studenta i jest stosowany, gdy dane mają rozkład normalny, a wariancja populacji jest nieznana.

Test t-Studenta wykorzystuje statystyki t, wartości rozkładu t i stopnie swobody do uzyskania wartości krytycznej dla danego poziomu istotności.

Ponadto krzywa rozkładu t może być aproksymowana przez krzywą normalną wraz ze wzrostem wielkości próby, która jest dalej klasyfikowana jako jednostronna (prawostronna i lewostronna) i dwustronna.

Istnieją różne rodzaje testów t, które można wykonać:

• Test t z jedną próbką;
• Dwupróbkowy test t-Studenta; oraz

* parowy test t-Studenta.

W następnej sekcji wyjaśnimy, kiedy używać którego z nich.
Pamiętaj, że test t-Studenta można zastosować tylko do jednej lub dwóch grup. Jeśli chcesz porównać trzy (lub więcej) średnie, użyj metody analizy wariancji (ANOVA).

Test t-Studenta jest testem parametrycznym, co oznacza, że Twoje dane muszą spełniać pewne założenia:

• Punkty danych są niezależne; ORAZ
• Dane, przynajmniej w przybliżeniu, mają rozkład normalny 🇺🇸.

Jeśli Twoja próba nie spełnia tych założeń, możesz skorzystać z alternatywnych testów nieparametrycznych, takich jak test U Manna-Whitneya lub test sumy rang Wilcoxona. Inne możliwości obejmują test rang z znamionami Wilcoxona lub test znaków.

Wybór testu t zależy od tego, czy badasz jedną grupę, czy dwie grupy:

• Jednopróbkowy test t-Studenta

  Wybierz test t z jedną próbką, aby sprawdzić, czy średnia populacji jest równa jakiejś wcześniej ustalonej wartości hipotezy.

  Przykłady:

  • Czy średnia objętość napoju sprzedawanego w puszkach o pojemności 0,33 l naprawdę wynosi 330 ml?

  • Średnia waga osób z określonego miasta – czy różni się od średniej krajowej?

• Dwuwymiarowy test t-Studenta

  Wybierz test t-Studenta dla dwóch próbek, aby sprawdzić, czy różnica między średnimi dwóch populacji jest równa jakiejś z góry określonej wartości, gdy obie próbki zostały wybrane niezależnie od siebie.

  W szczególności możesz użyć tego testu, aby sprawdzić, czy obie grupy różnią się od siebie.

  Przykłady:

  • Średnia różnica w przyroście masy ciała w dwóch grupach osób: jedna grupa była na diecie wysokowęglowodanowej, a druga na diecie wysokotłuszczowej.

  • Średnia różnica w wynikach testu z matematyki wśród studentów dwóch różnych uczelni.

  Test ten jest czasami nazywany testem t dla próbek niezależnych lub testem t dla próbek niesparowanych.

• Test t dla próbek sparowanych

  Sparowany test t służy do badania zmiany średniej populacji przed i po interwencji eksperymentalnej na podstawie próby sparowanej, tj. gdy każdy obiekt został zmierzony dwukrotnie: przed i po zabiegu.

  W szczególności można użyć tego testu, aby sprawdzić, czy w ujęciu średnim zabieg miał jakikolwiek wpływ na populację.

  Przykłady:

  * Zmiana wyników testów uczniów przed i po odbyciu kursu.

  • Zmiana ciśnienia krwi u pacjentów przed i po podaniu leku.

Wiesz już, który test t chcesz przeprowadzić. Kolejne kroki pokażą, jak obliczyć wartość p na podstawie testu t lub jego wartości krytycznych, a następnie jaką decyzję podjąć w sprawie hipotezy zerowej.

1. Wybierz hipotezę alternatywną:

   • Użyj dwustronnego testu t, jeśli interesuje Cię tylko to, czy średnia populacji (lub, w przypadku dwóch populacji, różnica między średnimi populacji) zgadza się lub nie zgadza z ustaloną wcześniej wartością.

   • Użyj jednostronnego testu t, jeśli chcesz sprawdzić, czy ta średnia (lub różnica średnich) jest większa/mniejsza niż wstępnie ustawiona wartość.

2. Oblicz wartość wyniku T:

   Wzory na statystykę testową w testach t obejmują wielkość próby, a także jej średnią i odchylenie standardowe. Dokładna formuła zależy od rodzaju testu t — więcej szczegółów znajdziesz w sekcjach poświęconych poszczególnym testom.

3. Określ stopnie swobody dla testu t:

   Stopnie swobody to liczba obserwacji w próbce, które mogą się zmieniać, gdy szacujemy parametry statystyczne. W najprostszym przypadku liczba stopni swobody jest równa wielkości próby pomniejszonej o liczbę parametrów, które trzeba oszacować. Ponownie dokładna formuła zależy od testu t, który chcesz przeprowadzić – szczegółowe informacje znajdziesz w poniższych sekcjach.

Stopnie swobody są niezbędne, ponieważ określają rozkład, za którym podąża wynik T (przy założeniu hipotezy zerowej). Jeśli istnieją d stopnie swobody, to rozkład statystyki testowej jest rozkładem t-Studenta z d stopniami swobody. Rozkład ten ma kształt podobny do N(0,1) (dzwonkowaty i symetryczny), ale ma cięższe ogony. Jeśli liczba stopni swobody jest duża (>30), co zazwyczaj ma miejsce w przypadku dużych próbek, rozkład t-Studenta jest praktycznie nie do odróżnienia od N(0,1).

Przypomnij sobie, że wartość p jest prawdopodobieństwem (obliczonym przy założeniu, że hipoteza zerowa jest prawdziwa), że statystyka testowa będzie generować wartości co najmniej tak ekstremalne, jak wynik T uzyskany dla Twojej próbki. Ponieważ prawdopodobieństwa odpowiadają obszarom pod funkcją gęstości, wartość p z testu t można ładnie zilustrować za pomocą następujących obrazków:

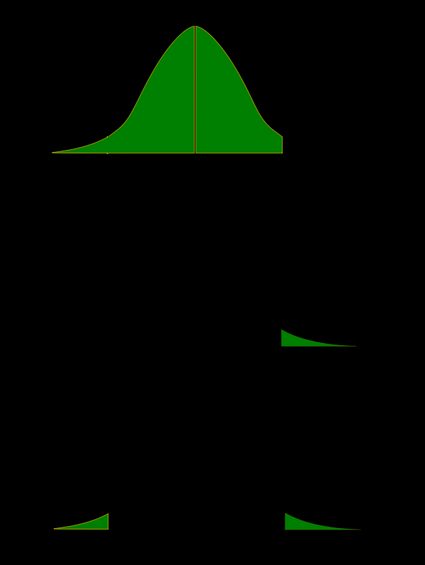
Poniższe wzory pokazują, jak obliczyć wartość p na podstawie testu t-Studenta. Przez cdf_t,d oznaczamy skumulowaną funkcję rozkładu rozkładu t-Studenta z d stopniami swobody:

1. Wartość p z lewoogoniastowego testu t-Studenta:

   wartość p = cdf_t,d(t_wynik)

2. Wartość p z prawostronnego testu t-Studenta:

   wartość p = 1 − cdf_t,d(t_wynik)

3. Wartość p z dwustronnego testu t-Studenta:

   wartość p = 2 × cdf_t,d(−|t_wynik|)

   lub, równoważnie: wartość p = 2 − 2 × cdf_t,d(|t_wynik|)

Jednak cdf rozkładu t jest podawane przez nieco skomplikowany wzór. Aby znaleźć wartość p ręcznie, musisz skorzystać z tabel statystycznych, w których zebrano przybliżone wartości cdf, lub ze specjalistycznego oprogramowania statystycznego. Na szczęście nasz kalkulator testu t określa wartość p z testu t w mgnieniu oka!

Przypomnijmy, że przed obliczeniem zbioru krytycznego testu t trzeba ustalić poziom istotności α. Na jego podstawie wyznaczamy wartości krytyczne.

Wzory na wartości krytyczne wykorzystują funkcję kwantyla rozkładu t, czyli funkcję odwrotną do dystrybuanty:

1. Wartość krytyczna dla lewego ogona testu t:
   cdf=t,d=^-1(α).

   Zbiór krytyczny:

   (-∞, cdf_t,d^-1(α)].

2. Wartość krytyczna dla prawego ogona:
   cdf_t,d^-1(1-α).

   Zbiór krytyczny:

   [cdf_t,d^-1(1-α), ∞).

3. Wartości krytyczne dla testu t dwustronnego:
   ±cdf_t,d^-1(1-α/2).

   Zbiór krytyczny:

   (-∞, -cdf_t,d^-1(1-α/2)] ∪ [cdf_t,d^-1(1-α/2), ∞).

Aby zdecydować o losie hipotezy zerowej, pozostaje sprawdzić, czy wartość statystyki testowej (t-score) należy do zbioru krytycznego:

• Jeśli t-score należy do zbioru krytycznego, odrzucamy hipotezę zerową i przyjmujemy hipotezę alternatywną.

• Jeśli t-score nie należy do zbioru krytycznego, to nie mamy podstaw, aby odrzucić hipotezę zerową.

1. Wybierz typ testu t, który chcesz wykonać:

   • Test t z jedną próbką (do testowania średniej pojedynczej grupy względem średniej hipotetycznej);

   • Dwupróbkowy test t-Studenta (do porównania średnich dla dwóch grup); lub

   * Test t dla próbek sparowanych (aby sprawdzić, jak zmienia się średnia z tej samej grupy po pewnej interwencji).

2. Wybierz hipotezę alternatywną:

   • Dwustronna;

   • lewostronny; lub

   • Prawostronny.

3. Ten kalkulator testu t pozwala użyć albo podejścia wartości p, albo podejścia regionów krytycznych do testowania hipotez!

4. Wprowadź wynik T i liczbę stopni swobody. Jeśli ich nie znasz, podaj dane o próbce (próbkach): wielkość próbki, średnią i odchylenie standardowe, a nasz kalkulator testu t obliczy dla Ciebie wynik T i stopnie swobody.

5. Po podaniu wszystkich parametrów wartość p lub obszar krytyczny pojawią się natychmiast pod kalkulatorem testu t wraz z interpretacją.

1. Hipoteza zerowa mówi, że średnia w populacji jest równa pewnej wartości $\mu_0$.

2. Hipoteza alternatywna mówi, że średnia w populacji jest:

   • różna od $\mu_0$;
   • mniejsza od $\mu_0$; lub
   • większa od $\mu_0$.

Wzór testu t dla jednej próbki:

gdzie:

• $\mu_0$ to średnia postulowana w hipoteze zerowej;
• $n$ to wielkość próby;
• $\bar{x}$ to średnia z próby; oraz
• $s$ to odchylenie standardowe próby.

Liczba stopni swobody w teście t dla jednej próbki wynosi $n-1$.

1. Hipoteza zerowa mówi, że rzeczywista różnica między średnimi tych grup, $\mu_1$ i $\mu_2$, jest równa jakiejś wstępnie ustalonej wartości $\Delta$.

2. Hipoteza alternatywna mówi, że różnica $\mu_1 - \mu_2$ jest:

   • różna od $\Delta$;
   • Mniejsza niż $\Delta$; lub
   • Większa niż $\Delta$.

W szczególności, jeśli ta z góry określona różnica wynosi zero ($\Delta = 0$):

1. Hipoteza zerowa mówi, że średnie populacji są równe.

2. Hipoteza alternatywna jest taka, że średnie populacji są następujące:

   • $\mu_1$ i $\mu_2$ różnią się od siebie;
   • $\mu_1$ jest mniejsze niż $\mu_2$; i
   • $\mu_1$ jest większa niż $\mu_2$.

Formalnie, aby przeprowadzić test t-Studenta, powinniśmy dodatkowo założyć, że wariancje obu populacji są równe (to założenie nazywa się * jednorodnością wariancji*).

Istnieje wersja testu t, którą można zastosować bez założenia jednorodności wariancji: nazywa się ją testem t-Welcha. Dla Twojej wygody opisujemy obie wersje.

Test t dla dwóch próbek, jeśli wariancje są równe

Użyj tego testu, jeśli wiesz, że wariancje dwóch populacji są takie same (lub bardzo podobne).

Wzór testu t dla dwóch próbek (przy równych wariancjach):

gdzie $s_p$ jest tzw. łącznym odchyleniem standardowym, które obliczamy jako:

oraz:

• $\Delta$ jest średnią różnicą postulowaną w hipotezie zerowej;
• $n_1$ jest liczebnością pierwszej próby;
• $\bar{x}_1$ jest średnią dla pierwszej próby;
• $s_1$ jest odchyleniem standardowym w pierwszej próbie;
• $n_2$ jest liczebnością drugiej próby;
• $\bar{x}_2$ jest średnią dla drugiej próby;
• $s_2$ jest odchyleniem standardowym w drugiej próbie.

Liczba stopni swobody w teście t (dwie próby, równe wariancje) wynosi $n_1 + n_2 - 2$.

Dwupróbkowy test t, jeśli wariancje niekoniecznie są równe (test t Welcha)

Użyj tego testu, jeśli wariancje twoich populacji są różne.

Wzór na test t dla dwóch prób Welcha, jeśli wariancje nie są równe:

gdzie:

• $\Delta$ jest średnią różnicą postulowaną w hipotezie zerowej;
• $n_1$ jest liczebnością pierwszej próby;
• $\bar{x}_1$ jest średnią dla pierwszej próby;
• $s_1$ jest odchyleniem standardowym w pierwszej próbie;
• $n_2$ jest liczebnością drugiej próby;
• $\bar{x}_2$ jest średnią dla drugiej próby; oraz
• $s_2$ jest odchyleniem standardowym w drugiej próbie.

Liczba stopni swobody w teście t Welcha (dwupróbkowym teście t z niekoniecznie równymi wariancjami) jest bardzo trudna do policzenia. Możemy ją przybliżyć za pomocą następującego wzoru Satterthwaite'a:

Alternatywnie można przyjąć mniejszą z liczb: $n_1 - 1$ oraz $n_2 - 1$ jako konserwatywne oszacowanie liczby stopni swobody.

Jako że najczęściej wykonujemy test t próbek sparowanych gdy mamy dane o tych samych osobach mierzonych dwukrotnie (przed i po jakimś leczeniu), przyjmijmy konwencję odnoszenia się do prób jako grupy „przed” i grupy „po”.

1. Hipoteza zerowa mówi, że prawdziwa różnica między średnimi populacji przed i po jest równa pewnej z góry ustalonej wartości, $\Delta$.

2. Hipoteza alternatywna głosi, że rzeczywista różnica między tymi średnimi jest:

   • różna od $\Delta$;
   • mniejsza od $\Delta$; lub
   • większa od $\Delta$.

Zazwyczaj ta wstępnie ustalona różnica wynosi zero. Możemy wtedy przeformułować hipotezy w następujący sposób:

1. Hipoteza zerowa mówi, że średnie przed i po są takie same, czyli leczenie nie ma wpływu na populację.
2. Hipoteza alternatywna mówi, że:
   • Średnie „przed” i „po” są różne od siebie (leczenie ma jakiś wpływ, ale nie wiemy czy pomaga, czy wręcz przeciwnie);
   • Średnia „przed” jest mniejsza od średniej „po” (leczenie zwiększa badany wynik); lub
   • Średnia „przed” jest większa od średniej „po” (leczenie zmniejsza wynik).

Wzór testu t sparowanego

Test t dla próbek sparowanych jest w rzeczywistości testem t dla jednej, odpowiednio przygotowanej, próbki! Załóżmy, że $x_1, \ldots , x_n$ to obserwacje wstępne („przed”), a $y_1, \ldots , y_n$ to obserwacje „po”. Przyjmujemy, że $x_i, y_i$ są pomiarami dla tego samego, i-tego, pacjenta.

Dla każdego pacjenta obliczamy różnicę, $d_i := x_i - y_i$. Wszystko, co dzieje się potem, to tylko jednopróbkowy test t wykonany na próbce różnic $d_1, \ldots , d_n$. Przyjrzyj się wzorowi na wynik t:

gdzie:

• $\Delta$ to średnia różnica postulowana przez hipotezę zerową;

• $n$ jest wielkością próby różnic, czyli liczbą par;

• $\bar{x}$ jest średnią z próby różnic; oraz

• $s$ jest odchyleniem standardowym próby różnic.

Liczba stopni swobody w teście t (sparowanym) wynosi $n - 1$.

Testu Z używamy, gdy chcemy sprawdzić średnią populacji w zbiorze danych o rozkładzie normalnym, który ma znaną wariancję populacji. Jeśli liczba stopni swobody jest duża, to rozkład t-Studenta jest bardzo zbliżony do N(0,1).

Zatem, jeśli masz do dyspozycji dużą próbkę (co najmniej 30 obserwacji), możesz zamienić test t na test Z, a wyniki będą prawie identyczne. Jednak w przypadku małych prób o nieznanej wariancji należy pamiętać o stosowaniu testu t, ponieważ rozkład t-Studenta różni się wtedy znacznie od rozkładu N(0,1)!