Kalkulator testu Z

Nasz kalkulator testu Z jest narzędziem, które pomoże ci wykonać jednopróbkowy test Z dla średniej w populacji. Może on wykonać dwie formy tego testu — dwustronny test Z i jednostronny test Z — w zależności od twoich potrzeb. Możesz także wybrać, czy kalkulator ma wyznaczyć wartość p z testu Z, czy raczej użyć wartości krytycznej.

Czytaj dalej, aby dowiedzieć się więcej o teście Z w statystyce, a w szczególności o tym, kiedy używać testu Z, jaki jest wzór na jego statystykę testową i jak ma się test Z do testu T studenta. Jako bonus podajemy kilka przykładów krok po kroku, jak wykonać test Z!

Możesz też sprawdzić nasz kalkulator wartości t, gdzie zapoznasz się z koncepcją innej istotnej statystyki testowej. Jeśli interesuje cię również test F, sprawdź nasz kalkulator testu F 🇺🇸.

Test Z dla jednej próby jest jednym z najpopularniejszych testów używanych w statystyce. Hipoteza zerowa mówi, że średnia wartość w populacji jest równa pewnej zadanej liczbie, $\mu_0$:

Wykonujemy dwustronny test Z, jeśli chcemy sprawdzić, czy średnia populacji jest w rzeczywistości inna niż $\mu_0$:

oraz jednostronny test Z, jeśli chcemy sprawdzić, czy średnia populacji jest mniejsza/większa niż $\mu_0$:

Omówimy teraz założenia testu Z.

Możesz użyć testu Z, jeśli twoja próbka jest prosta, tzn. składa się z niezależnych obserwacji oraz:

• dane mają rozkład normalny i znamy wariancję populacji;

  lub

• próba jest duża, a dane pochodzą z rozkładu o skończonej średniej i wariancji. Nie musisz znać tej wariancji!

Powodem istnienia tych dwóch możliwości jest fakt, że chcemy, aby statystyka testowa miała standardowy rozkład normalny $\mathrm N(0, 1)$. W pierwszym przypadku ma ona dokładnie taki rozkład, podczas gdy w drugim będze on taki z dobrym przybliżeniem, dzięki centralnemu twierdzeniu granicznemu (CTG)

Pozostaje pytanie: „Kiedy moja próbka jest uważana za dużą?” Cóż, nie ma na to uniwersalnego kryterium. Ogólnie rzecz biorąc, im więcej obserwacji, tym lepiej. Podręczniki statystyki zalecają nie mniej niż 50 elementów, podczas gdy 30 jest uważane za absolutne minimum, aby korzystać z przybliżenia poprzez CTG.

Załóżmy, że $x_1, ..., x_n$ to nasza próbka o rozkładzie normalnym $\mathrm N(\mu, \sigma^2)$, tj. o średniej równej $\mu$ i wariancji równej $\sigma^2$.

Stawiamy hipotezę zerową $\mathrm H_0 \!\!:\!\! \mu = \mu_0$ i definiujemy statystykę testową Z jako:

gdzie:

• $\bar x$ jest średnią z próby, tj. $\bar x = (x_1 + ... + x_n) / n$;

• $\mu_0$ jest średnią wyrażoną w hipotezie $\mathrm H_0$;

• $n$ jest wielkością próby;

• $\sigma$ jest odchyleniem standardowym w populacji.

W dalszej części tekstu wielka litera $Z$ oznacza statystykę testową (traktowaną jako zmienna losowa), podczas gdy mała litera $z$ oznacza realizację tej zmiennej, tzn. wartość obliczoną dla danej próbki danych wylosowanych z N(μ,σ²).

Przy założeniu prawdziwości $\mathrm H_0$, suma $S_n = x_1 + ... + x_n$ ma rozkład normalny ze średnią $n \mu_0$ i wariancją $n^2 \sigma$. Ponieważ $Z$ jest standaryzacją $S_n/n$, możemy stwierdzić, że statystyka testowa $Z$ ma standardowy rozkład normalny $\mathrm N(0, 1)$, pod warunkiem prawdziwości $\mathrm H_0$. Przy okazji, mamy kalkulator standaryzacji, jeśli chcesz dowiedzieć się o tym więcej.

Jeśli nasze dane nie pochodzą z rozkładu normalnego lub jeśli odchylenie standardowe populacji jest nieznane (a zatem we wzorze na $Z$ zastępujemy odchylenie standardowe populacji $\sigma$ odchyleniem standardowym próby), wówczas statystyka testowa $Z$ niekoniecznie ma rozkład normalny. Jednakże, jeśli próba jest wystarczająco duża, wówczas centralne twierdzenie graniczne gwarantuje, że rozkład $Z$ to w przybliżeniu $\mathrm N(0, 1)$.

W kolejnych sekcjach wyjaśnimy ci jak wykorzystać wartość statystyki testowej, $z$, do podjęcia właściwej decyzji odnośnie odrzucenia (bądź nie) hipotezy zerowej. Aby podjąć taką decyzję, możesz skorzystać z dwóch podejść: wartości p lub wartości krytycznej — omówimy oba te zagadnienia!

A którego z nich powinieneś/powinnaś użyć? W przeszłości podejście oparte na wartości krytycznej było bardziej popularne, ponieważ ręczne obliczanie wartości p (p-wartości) z testu Z jest trudne. Jednak z pomocą współczesnych komputerów możemy to zrobić łatwo, szybko i z przyzwoitą precyzją. Ogólnie rzecz biorąc, zdecydowanie zalecamy podawanie p-wartości testów statystycznych.

Formalnie, wartość p (p-wartość lub z ang. p-value) jest najmniejszym poziomem istotności, przy którym hipoteza zerowa może zostać odrzucona. Bardziej intuicyjnie, wartość p odpowiada na następujące pytanie:

Zakładając, że żyję w świecie, w którym hipoteza zerowa jest prawdziwa, jak prawdopodobne jest, że wartość statystyki testowej będzie co najmniej tak skrajna, jak wartość $z$, którą otrzymałem/am dla mojej próbki?

Zatem bardzo mała wartość p oznacza, że twój wynik jest bardzo nieprawdopodobny gdyby hipoteza zerowa była prawdą, a więc mała p-wartość stanowi dowód przeciwko prawdziwości hipotezy zerowej — im mniejsza p-wartość, tym mocniejszy ten dowód.

Aby znaleźć wartość p, musisz obliczyć prawdopodobieństwo, że statystyka testowa $Z$ może przyjąć wartość co najmniej tak ekstremalną jak wartość $z$, którą faktycznie zaobserwowaliśmy, przy założeniu prawdziwości hipotezy zerowej. (Prawdopodobieństwo zdarzenia obliczone przy założeniu, że $\mathrm H_0$ jest prawdziwa, będzie oznaczane jako $\small \mathrm{Pr}(\text{zdarzenie} | \mathrm{H_0})$.) Hipoteza alternatywna służy do określenia, co oznacza wartość bardziej ekstremalna:

1. Dwustronny test Z: wartości ekstremalne to te, których wartość bezwzględna przekracza $|z|$, a więc te mniejsze niż $-|z|$ lub większe niż $|z|$. Dlatego mamy:

Zaś z symetrii rozkładu normalnego wynika, że:

2. Lewostronny test Z: wartości ekstremalne są mniejsze niż $z$, więc

3. Prawostronny test Z: wartości ekstremalne są większe niż $z$, więc

Aby obliczyć te prawdopodobieństwa, możemy użyć dystrybuanty rozkładu $\mathrm N(0, 1)$, która dla liczby rzeczywistej, $x$, jest zdefiniowana jako:

Ponadto, wartości p mogą być przedstawione jako pole pod wykresem funkcji gęstości rozkładu $\mathrm N(0, 1)$, gdyż:

Z całą wiedzą zdobytą w poprzedniej sekcji, jesteś gotowy/a, aby dowiedzieć się więcej o rodzajach testu Z.

1. Dwustronny test Z:

Wiedząc, że $\Phi(-z) = 1 - \Phi(z)$, możemy wywnioskować, że:

Wartość p to obszar pod wykresem funkcji gęstości rozkładu zarówno na lewo od $-|z|$, jak i na prawo od $|z|$:

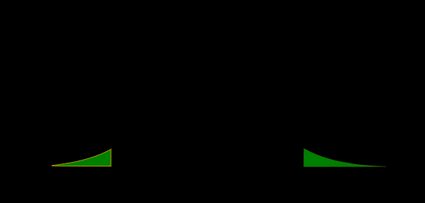
2. Lewostronny test Z:

Wartość p to obszar pod wykresem gęstości na lewo od $z$:

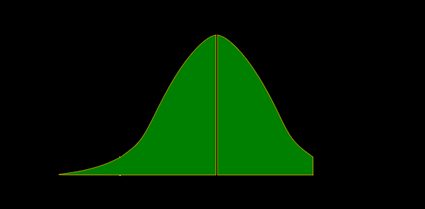
3. Prawostronna wartość p

Wartość p to obszar pod wykresem gęstości na prawo od $z$:

Gdy znasz wartość p, decyzja o tym, czy należy odrzucić hipotezę zerową, może być teraz podjęta na dowolnym ustalonym poziomie istotności, $\alpha$!

• jeśli wartość p jest mniejsza lub równa $\alpha$, hipoteza zerowa jest odrzucana na tym poziomie istotności.

• jeśli wartość p jest większa niż $\alpha$, to nie ma wystarczających dowodów, aby odrzucić hipotezę zerową na tym poziomie istotności.

Podejście poprzez wartości krytyczne polega na porównaniu wartości statystyki testowej uzyskanej dla naszej próbki, $z$, z tak zwanymi wartościami krytycznymi. Wartości te odpowiadają obszarom, w których prawdopodobieństwo wystąpienia statystyki testowej jest bardzo niskie. Obszary te są często nazywane obszarami krytycznymi lub obszarami odrzucenia. Decyzja o tym, czy odrzucić hipotezę zerową, opiera się na tym, czy nasze $z$ należy do obszaru krytycznego, czy też do niego nie należy.

Obszary krytyczne zależą od poziomu istotności, $\alpha$, i od rozważanej hipotezy alternatywnej. Wybór $\alpha$ jest arbitralny; w praktyce jako $\alpha$ najczęściej przyjmujemy 0,05 lub 0,01, rzadziej 0,1.

Gdy już ustalimy wartość $\alpha$, możemy łatwo określić obszary krytyczne testu Z:

1. Dwustronny test Z:

2. Lewostronny test Z:

Prawostronny test Z:

Aby zdecydować o losie $\mathrm H_0$, sprawdź, czy twoja wartość $z$ znajduje się w obszarze krytycznym:

• Jeśli tak, odrzuć $\mathrm H_0$ i zaakceptuj $\mathrm H_1$.

• Jeśli nie, to nie masz wystarczających powodów, aby odrzucić $\mathrm H_0$.

Jak widzisz, we wzorach na wartości krytyczne testów Z pojawia się odwrotność dystrybuanty rozkładu $\mathrm N(0, 1)$, czyli funkcja $\Phi^{-1}$.

Nasz kalkulator redukuje wszystkie skomplikowane kroki:

1. Wybierz hipotezę alternatywną: dwustronną lub lewostronną/prawostronną.

2. W naszym kalkulatorze testu Z możesz zdecydować, czy użyć wartości p, czy obszarów krytycznych. W tym drugim przypadku podaj poziom istotności, $\alpha$.

3. Wprowadź wartość statystyki testowej, $z$. Jeśli jej nie znasz, możesz wprowadzić dane, które pozwolą nam obliczyć $z$:

   • średnia z próby $\bar x$ (jeśli masz tylko surowe dane, przejdź do kalkulatora średniej, aby ją obliczyć);
   • testowana średnia $\mu_0$;
   • wielkość próby $n$;
   • odchylenie standardowe populacji $\sigma$ (lub odchylenie standardowe próby, jeśli twoja próba jest duża).

4. Wyniki pojawią się bezpośrednio pod kalkulatorem.

Jeśli chcesz znaleźć $z$ na podstawie wartości p, pamiętaj, że w przypadku testów dwustronnych istnieją dwie możliwe wartości $z$: jedna dodatnia i jedna ujemna, i są to liczby sobie przeciwne. Kalkulator testu Z zwraca w takim przypadku wartość dodatnią. Aby znaleźć drugą możliwą wartość $z$ dla danej wartości p, po prostu weź liczbę przeciwną do wartości $z$ wyświetlanej przez kalkulator.

Aby upewnić się, że w pełni rozumiesz istotę testu Z, przejdźmy przez kilka przykładów:

1. Maszyna napełnia butelki zgodnie z rozkładem normalnym. Jej odchylenie standardowe, zgodnie z deklaracją producenta, wynosi 30 ml. Sprzedawca soku twierdzi, że objętość wlewana do każdej butelki wynosi średnio jeden litr, tj. 1000 ml, ale podejrzewamy, że w rzeczywistości średnia objętość jest mniejsza niż wskazana.

Formalnie, hipotezy które stawiamy, są następujące:

• $\mathrm H_0 \! : \mu = 1000 \text{ ml}$

• $\mathrm H_1 \! : \mu \lt 1000 \text{ ml}$

Poszliśmy do sklepu i kupiliśmy 9 butelek tego soku. Po dokładnym zmierzeniu objętości soku w każdej butelce otrzymaliśmy następującą próbkę (w mililitrach):

$\small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980$.

• Wielkość próbki: $n = 9$;

• Średnia z próby: $\bar x = 980 \ \mathrm{ml}$;

• Odchylenie standardowe populacji: $\sigma = 30 \ \mathrm{ml}$;

• A zatem:

• Dlatego też $\text{wartość p} = \Phi(-2) \approx 0,\!0228$.

  Wynik $0,\!0228$ oznacza, że nasze podejrzenia nie są bezpodstawne; na najbardziej powszechnym poziomie istotności, 0,05, odrzucilibyśmy twierdzenie producenta, $\mathrm H_0$, i zaakceptowalibyśmy hipotezę alternatywną, $\mathrm H_1$.

2. Rzuciliśmy monetą 50 razy. Otrzymaliśmy 20 reszek i 30 głów. Czy jest to wystarczający dowód, aby twierdzić, że moneta jest niesymetryczna?

   Oczywiście nasze dane są zgodne z rozkładem Bernoulliego, z pewnym prawdopodobieństwem sukcesu $p$ i wariancją $\sigma^2 = p (1-p)$. Jednak próba jest duża, więc możemy bezpiecznie przeprowadzić test Z. Przyjmujemy konwencję, że wyrzucenie reszki oznacza sukces.

   Podaj hipotezę zerową i alternatywną:

   • $\mathrm H_0 \! : p = 0,5$

   (moneta jest symetryczna: prawdopodobieństwo wyrzucenia reszki wynosi $0,\!5$)

   • $\mathrm H_1 \! : p \ne 0,5$

   (moneta jest niesymetryczna: prawdopodobieństwo wyrzucenia reszki różni się od $0,5$)

W naszej próbie mamy 20 sukcesów (oznaczonych jedynkami) i 30 porażek (oznaczonych zerami), więc:

• Wielkość próby $n = 50$;

• Średnia próbki $\bar x = 20/50 = 0,\!4$;

• Odchylenie standardowe populacji wynosi $\sigma = \sqrt{0,\!5 \cdot 0,\!5}$ (ponieważ $0,\!5$ jest wartością $p$ założoną w $\mathrm H_0$). Stąd, $\sigma = 0,\!5$;

• Zatem

• Czyli

Ponieważ $0,\!1573 \gt 0,\!1$ nie mamy wystarczających dowodów, aby odrzucić twierdzenie, że moneta jest symetryczna, nawet na tak wysokim poziomie istotności jak $0,\!1$. W takim przypadku możemy na przykład użyć kalkulatora prawdopodobieństwa rzutu monetą, aby znaleźć swoje szanse na uzyskanie np. 10 reszek z rzędu (które są niezwykle niskie!).