Prisoner's Dilemma Calculator

With our prisoner's dilemma calculator you will learn the basics of game theory. Keep reading this comprehensive article to learn:

• What is game theory: the framework for the prisoner's dilemma.
• Description of a game: the prisoner's dilemma.
• Strategies in the prisoner dilemma: betrayal!
• Emergence of kindness: calculating the prisoner's dilemma's outcome in an iterated tournament.

Game theory is a mathematical framework that deals with decisions and their outcomes. A game is a situation where two or more agents (the players) are tasked with making a decision. Game theory can predict the behaviors and the consequences of the actions of these agents, laying down the strategies of the players: ideal choices that lead to well-defined results.

Let's start then: what is a game in game theory? What are the elements of a game? Let's discover our first game, the prisoner's dilemma.

Imagine two criminals getting arrested for a minor felony. During their interrogation, they are kept separated, and the police give both of them a choice:

• Stay silent; or
• Confess.

These are the two possible strategies for each player. In game theory, the decision-making process is controlled by the result of each combination of strategies. This result is called payoff. Each player has a payoff associated with each pair of strategies.

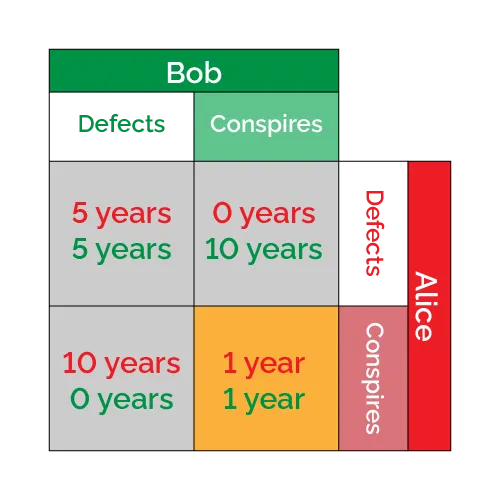
Let's consider one of the players. Let's call her Alice:

• If she confesses and the other player (Bob) confesses, they both get a hefty punishment. This payoff is marked with $\mathrm{P}$ for punishment.

• If she stays silent, and Bob keeps up with the silence too, the lack of evidence allows them to get away with the payoff $\rm R$, a reward for cooperation.

• If she confesses and the other player stays silent, she gets away freely (payoff of the traitor $\rm T$) while her accomplice receives the heaviest punishment (the sucker's payoff $\rm S$).

• The last scenario happens in reverse if Alice stays silent and her accomplice confesses.

The four payoffs identified above must satisfy the inequality $\rm T>R>P>S$ if we want the game to be a game of prisoner's dilemma. Other relationships between payoffs would result in other games with vastly different winning strategies and outcomes.

Mathematicians created a helpful notation for this setup, the payoff matrix. We discussed this matrix formalism thoroughly in our matrix calculator. In this notation, the possible strategies of the players and the relative payoffs are neatly arranged.

Which strategy will the player choose? If you think that the answer is cooperation, then you are wrong!

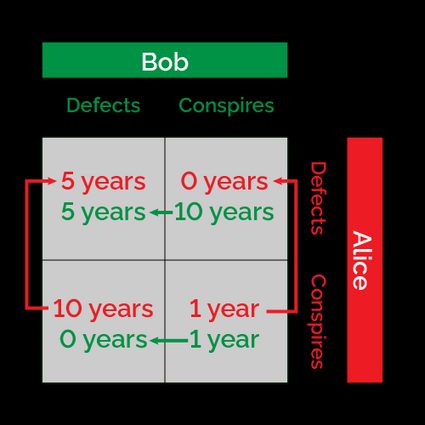
In the game theory framework, the players are rational and play with the unique intention of increasing their payoff. This will lead them to necessarily betray their partners. The outcome? Both of them will confess and receive a relatively severe punishment. The final combination of payoffs associated with a combination of strategies is called Nash equilibrium of the game.

We can easily find the Nash equilibrium by looking at the payoff matrix and following the arrows that indicate the direction of maximization of the individual payoffs. If each player chooses a strategy that maximizes their payoff, then their decision will move necessarily from cooperation to betrayal. Let's dive deeper into the prisoner dilemma's mathematics!

Let's assign numbers to the payoffs identified in the previous sections. By following the inequality, we can decide that the values of each variable will be a certain amount of prison time. The lower the imprisonment time, the better (the ideal best payoff is $0$), so we will assign to the variables negative numbers or $0$. A possible combination is:

• $\rm T =0$ (the traitor gets away without spending a day in jail);
• $\rm R = -1$ (if both prisoners cooperate, they spend minimal time in jail);
• $\rm P = -5$ (both players receive a substantial punishment in case of confession); and
• $\rm S = -10$ (in this case, the player that stays silent while the other defects receive the severest punishment).

Arrange these payoffs in the matrix now, and identify how strategy changes by both players affect their payoffs.

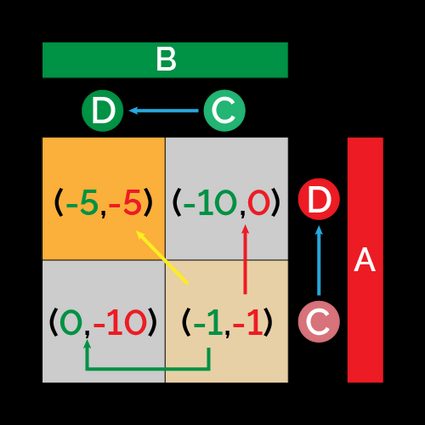
• If both players start cooperating, they would quickly change their minds, as a simple change in decision to defect may cause their individual payoff to grow from $-1$ to $0$.

• If Alice starts cooperating, but Bob defects, he would begin with payoff $0$, and she would start with payoff $-10$: of course, the best strategy for Alice is to switch to defect, in an attempt to increase her payoff.

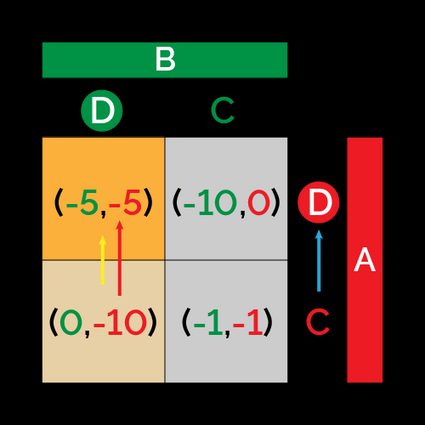
• If Alice starts defecting while Bob cooperates, Alice will not change her mind (as she begins with payoff $0$), while Bob will switch to defect trying to reduce the sucker's payoff ($-10$) to something better.

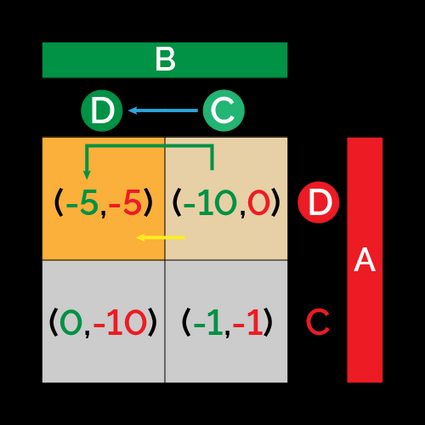
• If both players start defecting, they have no reason to change their decisions: in their minds, their payoffs are the highest possible! This combination of strategies is even easier to understand if we consider what would happen if they both changed strategy: their payoff would switch from $-5$ to $-10$. Why would anyone do this?

What is the common picture we get from these scenarios? Both players will defect in an attempt to maximize their payoffs. Arrows in the matrix of the payoffs represent the possible changes in decisions.

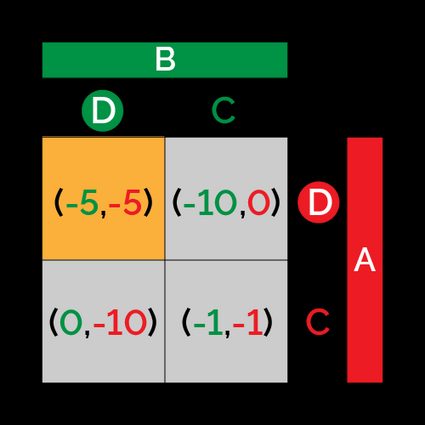
As all possible initial combinations of strategies lead to the same outcome after the players are allowed to change their decisions, we say that the final result of these adjustments is a stable point of the game, or, in technical language, a Nash equilibrium.

A Nash equilibrium is a solution to a game in the form we presented above. By definition, a Nash equilibrium corresponds to the set of strategies (one for each player) for which each agent, assuming that the other plays the strategy of the equilibrium, won't increase its payoff by changing strategy.

More often than not, Nash equilibriums are not optimal. In the case of the prisoner's dilemma, it corresponds to the situation in which both prisoners confess the crime. In this case, if one of them changed strategy, it would receive the sucker's payoff; thus, there is no motivation to change it. Considering the optimal solution where both players cooperate, we can see that each can increase the payoff by changing strategy (hence they both will do this!).

A game can have no Nash equilibriums (rock, paper, scissor is an example of such a situation), one or multiple equilibriums.

The last section may have left us with a bitter taste: are our decisions dictated by selfishness? Given a choice, will we betray and be betrayed regardless of everything else?

The answer is, luckily, no. A single instance of the prisoner dilemma leads us to this seemingly counterintuitive solution. Still, as soon as we start playing this game repeatedly, creating and adapting repeated strategies according to the other player's behavior, the outcome changes significantly. We are now dealing with the iterated prisoner dilemma.

The setup is the same as before, but we calculate a cumulative payoff this time. If there is no specified time limit, we introduce a coefficient that reduces the payoff of games as the tournament proceeds. Mathematically speaking, we multiply the payoff of the round $n$ by $\delta^n$, where $\delta$ is a number between $0$ (fast reduction of the payoff) and $1$ (the payoff decreases slowly). This mechanism is akin to what we met at our geometric sequence calculator.

Strategies in the iterated prisoner dilemma describe how an "automaton" acts depending on its rules. Automata can react to other strategies, such as being kind (cooperative), retaliatory, forgiving, etc.

The strategy that describes the original outcome of the prisoner's dilemma game is called AllD, for all defection. Regardless of the initial state and the opponent's strategy, an AllD automaton always defects. Surprisingly, this is not the best strategy for the iterated prisoner's dilemma.

Suppose a player stays nice for the time being, but retaliates with defection as soon as the opponent defects and never changes its strategy again. In that case, it's using the grim or trigger strategy. This strategy is marginally better than AllD, but it is still far from optimal.

The actual winner of this prisoner's dilemma tournament is a forgiving strategy with a hint of retaliation. The name of this automaton is tit for tat, and it simply copies the opponent's last move. If the opponent defects, tit for tat defects, and keeps doing so until the opponent changes their mind. In that case, tit-for-tat defects one last time (as the decisions are simultaneous) take a higher payoff and forgive.

The tit-for-tat automaton can assume various forms, more or less retaliating, more or less forgiving. Discover them in our tool!

Our prisoner's dilemma calculator implements the simple and iterated prisoner's dilemma game.

• In the simple prisoner's dilemma, choose the strategy of both players. We will mark the starting point and tell you how the game will evolve from there, proving to you that the betrayal is all but avoidable.

• In the iterated prisoner's dilemma, you can choose two strategies among a rather furnished list and the discount rate on the payoffs. We will print the payoff toward which the strategies converge.

The prisoner's dilemma is the most famous example of a game in game theory. It describes a situation where two criminals are faced with various punishments, the entity of which depends on the interaction between the choices of the two players. If the prisoners are rational, the decision they will eventually take is not the one that minimizes the punishment for both of them but the one that follows selfish decisions.

The winning strategy in the prisoner's dilemma is not the one that leads to the optimal outcome for the players. As defection gives a chance for a player to receive the maximum payoffs, both prisoners will confess their crimes, leading to a situation where the payoff is far from optimal for both of them. Intuitively, we would think that a cooperative strategy would fare better, but this is not true.

If a game of prisoner's dilemma is iterated multiple times, repeated defection strategies tend not to fare well, as they often lead to significant losses. Cooperation is rewarded with a gentler punishment: in the case of iterated games, cooperative strategies tend to score higher payoffs by mutual agreement. This emergence of kindness models behavior seen normally in real life.

A single iteration of the prisoner's dilemma is not always realistic. The outcome, both players confessing and receiving strong punishment, is likely only if multiple conditions are met:

• The players are selfish and rational (hence they try to maximize their payoffs);
• The players have complete information; and
• There is no communication.

Once these conditions are met, it's possible that selfish behavior would fare better than cooperative ones, but in real life, it is much more common to witness some degree of cooperation.