Calculadora de Triângulos 30 60 90

Com essa calculadora de triângulo 30 60 90 da Omni, você pode resolver as medidas desse triângulo retângulo especial. Se estiver procurando a fórmula do triângulo 30 60 90 para a hipotenusa, se estiver se perguntando sobre a razão do triângulo 30 60 90 ou simplesmente quiser visualizar esse triângulo, você veio ao lugar certo. Continue lendo a página para saber mais sobre esse triângulo retângulo ou confira também outras ferramentas similares, a calculadora de triângulo retângulo e a calculadora de triângulos 45 45 90 da Omni.

Antes de mais nada, vamos explicar o que significa "30 60 90". Quando escrevemos sobre o triângulo 30 60 90, estamos nos referindo aos ângulos do triângulo, que são iguais a 30°, 60° e 90°.

Suponha que o lado mais curto de um triângulo 30 60 90 seja igual a a. Então:

• O segundo lado é igual a a√3;
• A hipotenusa é 2a;
• A área é igual a a²√3/2; e
• O perímetro é igual a a(3 + √3).

As fórmulas dos triângulos 30 60 90 são bem fáceis, mas qual é a matemática por trás delas? Vamos verificar quais métodos você pode usar para prová-las:

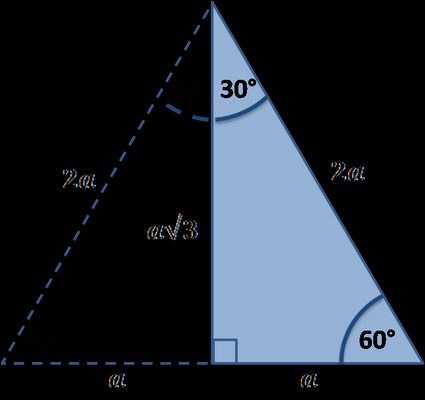
1. Usando as propriedades do triângulo equilátero

Você notou que nosso triângulo de interesse é simplesmente a metade do triângulo equilátero? Se você não conhece esse tipo de triângulo, consulte a calculadora de triângulo equilátero da Omni. Caso você lembre a fórmula para a altura de um triângulo regular, saberá também o comprimento do segundo lado. Ele é igual ao lado vezes a raiz quadrada de 3, dividido por 2:

h = c√3/2, h = b e c = 2a, portanto b = c√3/2 = a√3

2. Usando trigonometria

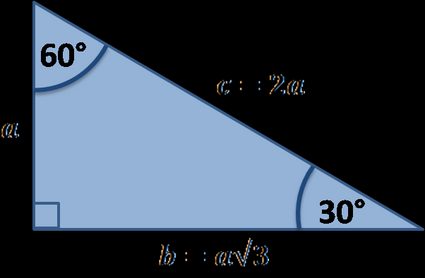
Se você estiver familiarizado com as noções básicas de trigonometria, poderá usar, por exemplo, o seno e o cosseno de 30° para descobrir os comprimentos dos outros lados:

a/c = sen(30°) = 1/2, portanto c = 2a

b/c = sen(60°) = √3/2 então b = c√3/2 = a√3

Além disso, se você souber dois lados do triângulo, poderá encontrar o terceiro a partir do teorema de Pitágoras (a calculadora do teorema de Pitágoras da Omni poderá te ajudar com isso). No entanto, os métodos descritos acima são mais úteis, pois você precisa conhecer apenas um lado do triângulo 30 60 90.

Se soubermos o comprimento do lado menor a, poderemos descobrir que:

• b = a√3

• c = 2a

Se o comprimento do lado maior b for o único parâmetro fornecido, então:

• a = b√3/3

• c = 2b√3/3

Para a hipotenusa "c" conhecida, as fórmulas dos lados a e b são as seguintes:

• a = c/2

• b = c√3/2

Ou simplesmente digite os valores que você forneceu e a calculadora de triângulos 30 60 90 fará o resto!

A regra mais importante a ser lembrada é que esse triângulo retângulo especial tem um ângulo reto e seus lados estão em uma relação consistente e fácil de lembrar entre si, ou seja, sua proporção é a : a√3 : 2a. Além disso, a propriedade diferenciada desse triângulo 30 60 90 é que ele é o único triângulo retângulo com ângulos em uma progressão aritmética.

O que é uma progressão aritmética? Consulte nossa calculadora de progressão aritmética para saber mais!

No triângulo 30 60 90, as proporções são:

• 1 : 2 : 3 para os ângulos (30° : 60° : 90°); e
• 1 : √3 : 2 para os lados (a : a√3 : 2a).

Você leu sobre as regras do triângulo 30 60 90. Agora é hora de praticar!

1. Digite o valor do lado. Digamos que você queira verificar como resolver o triângulo 30 60 90 do nosso conjunto de esquadros. Há uma escala no lado mais longo. Suponha que seu comprimento seja de b = 32 cm.
2. Insira o valor de b na calculadora. Graças a esta calculadora de triângulos 30 60 90, você verá que todos os outros valores aparecem.

• O lado menor tem 18,48 cm porque a = b√3/3 = 32 cm ⋅ √3/3 ~ 18,48 cm.
• A hipotenusa é igual a 36,95 cm porque c = 2b√3/3 = 2a ~ 36,95 cm.
• A área é de 295,6 cm²². Este é o resultado da multiplicação do comprimento dos lados e da divisão por 2: área = a²√3 ≈ 295,6 cm².
• O perímetro é igual a 87,4 cm, pois a adição de todos os lados dá esse resultado perímetro = a + a√3 + 2a = a(3 + √3) ≈ 87,4 cm.