Last updated: Apr 30, 2024

Calculadora de Triângulos Retângulos Especiais

Q: Quais são as fórmulas para um triângulo 45 45 90?

Um triângulo 45° 45° 90° tem as seguintes fórmulas, em que x é o comprimento de qualquer um dos lados iguais: Hipotenusa = x√2 ; Área = x²/2 ; e Perímetro = x(2+√2) . Read more

Q: 3, 4 e 5 é um terno pitagórico?

Sim . Os números inteiros a = 3 , b = 4 e c = 5 formam um terno pitagórico, pois a² + b² = c² e um triângulo com lados abc é um triângulo retângulo especial. Read more

Table of contents

Triângulos retângulos especiais 30 60 90 Triângulos retângulos especiais 45 45 90 Outros triângulos retângulos especiais Fórmulas especiais de triângulos retângulos Regras especiais para triângulos retângulos Calculadora de triângulo retângulo especial: exemplo FAQs

Essa calculadora de triângulos retângulos especiais é uma ferramenta da Omni que ajudará você a encontrar as medidas de um triângulo retângulo em um piscar de olhos. Selecione o triângulo que você precisa e digite os valores fornecidos. Os parâmetros restantes serão calculados automaticamente.

Os triângulos retângulos especiais são triângulos retângulos para os quais existem fórmulas simples. Isso permite cálculos rápidos, de modo que você não precisa usar o teorema de Pitágoras ou algum método mais avançado. Role para baixo para ler mais sobre as fórmulas e regras de triângulos retângulos especiais.

Triângulos retângulos especiais 30 60 90

O triângulo retângulo especial $30\degree$ $60\degree$ $90\degree$ é um dos triângulos retângulos mais populares. Suas propriedades são únicas e ele corresponde a metade de um triângulo equilátero. A Omni também tem disponível uma calculadora de trinângulo equilátero, caso você queira conferir.

Se você quiser saber mais sobre esse tipo de triângulo, consulte nossa calculadora de triângulos 30 60 90 dedicada.

Triângulos retângulos especiais 45 45 90

Outro triângulo retângulo especial famoso é o $45\degree$ $45\degree$ $90\degree$ . Ele é o único triângulo que é retângulo e isósceles ao mesmo tempo. Além disso, é a forma criada quando cortamos um quadrado ao longo da sua diagonal:

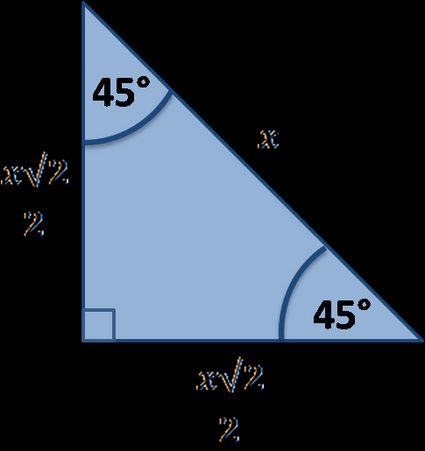
Você está curioso sobre as propriedades desse triângulo? Dê uma olhada na calculadora de triângulos 45 45 90 ou na calculadora de triângulo isósceles, ambas da Omni.

Outros triângulos retângulos especiais

Existem muitos triângulos retângulos especiais. Abaixo, você encontrará os que foram implementados em nossa ferramenta:

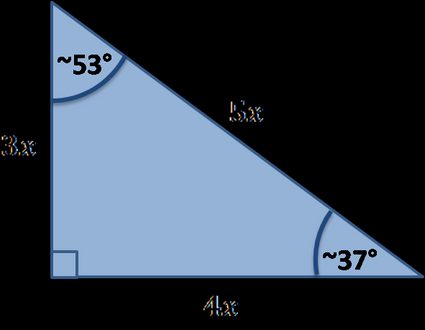
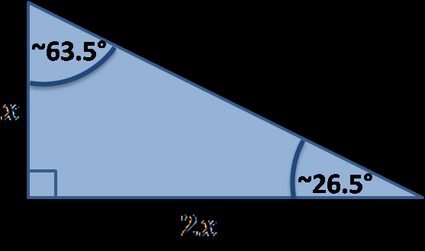
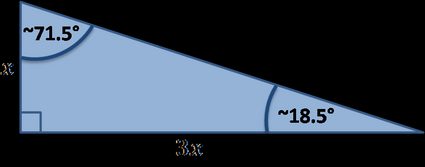
Fórmulas especiais de triângulos retângulos

triângulo retângulo com lados a,b,c e ângulos α, β

Se estiver procurando as fórmulas para triângulos retângulos especiais, você está no lugar certo. Veja a tabela abaixo; tudo deve estar claro! Nessa tabela, você encontrará as fórmulas para a relação entre ângulos, catetos, hipotenusa, área e perímetro de triângulos retângulos especiais:

Triângulo Retângulo	$a$ (lado menor)	$b$ (lado maior)	$c$ (hipotenusa)	Área	Perímetro	Ângulo $\alpha$	Ângulo $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x - 2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\sim26.5\degree$	$\sim63.5\degree$
$x - 3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\sim18.5\degree$	$\sim71.5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\sim37\degree$	$\sim53\degree$

Regras especiais para triângulos retângulos

Os triângulos retângulos especiais são aqueles que têm algumas características específicas que facilitam os cálculos. Obviamente, a regra mais importante dos triângulos retângulos especiais é que eles precisam ter um ângulo reto e uma característica extra. Em geral, os triângulos retângulos especiais podem ser divididos em dois grupos, de acordo com:

Seus ângulos: por exemplo, os triângulos $30\degree$ - $60\degree$ - $90\degree$ e $45\degree$ - $45\degree$ - $90\degree$ .
Seus lados: figuras que têm comprimentos de lados governados por uma regra específica, por exemplo:
- Lados com comprimentos inteiros chamados ternos pitagóricos:
  
  $3:4:5$ , $5:12:13$ , $8:15:17$ , $7:24:25$ , $9:40:41$ ...
- Lados com comprimentos inteiros, mas quase isósceles:
  
  $20:21:29$ , $119:120:169$ , $696:697:985$ ...
- Triângulo retângulo, cujos lados estão em uma progressão geométrica (triângulo de Kepler). Seus lados são formados a partir dos lados de três quadrados. Suas áreas estão em progressão geométrica, de acordo com a proporção áurea, mais conhecida como razão de ouro. Para saber mais sobre essa proporção especial, acesse nossa calculadora da razão de ouro.

Há muitas regras e opções diferentes pelas quais podemos escolher o triângulo e chamá-lo de especial. Em nossa calculadora de triângulos retângulos especiais, implementamos cinco triângulos escolhidos: dois baseados em seus ângulos e três baseados em seus lados.

Calculadora de triângulo retângulo especial: exemplo

Vamos dar uma olhada no exemplo: queremos encontrar o comprimento da hipotenusa de um triângulo retângulo se o comprimento de um lado for $5$ cm e um ângulo for $45\degree$ .

Escolha o tipo adequado de triângulo retângulo especial. No nosso caso, é o triângulo $45\degree$ - $45\degree$ - $90\degree$ .
Digite o valor fornecido. Sabemos que o lado é igual a $5$ cm, portanto, digitamos esse valor na caixa a ou b (nesse caso, não importa onde, pois se trata de um triângulo isósceles).
Uau! A calculadora de triângulos retângulos especiais resolveu as medidas do seu triângulo! Podemos ver que:
- O segundo lado $b$ é igual a $5\ \mathrm{cm}$ ;
- A hipotenusa $c$ é $7,\!07\ \mathrm{cm}$ ;
- O perímetro é igual a $17,\!07\ \mathrm{cm}$ ; e
- A área do nosso triângulo especial é $12,\!5\ \mathrm{cm^2}$ .

O que você está esperando? Tente encontrar os mesmos resultados usando a nossa calculadora!

FAQs

Quais são as fórmulas para um triângulo 45 45 90?

Um triângulo 45° 45° 90° tem as seguintes fórmulas, em que x é o comprimento de qualquer um dos lados iguais:

Hipotenusa = x√2;
Área = x²/2; e
Perímetro = x(2+√2).

Como resolver um triângulo retângulo especial 30 60 90?

Para resolver um triângulo retângulo especial de 30° 60° 90°, siga estas etapas:

Encontre o comprimento do menor lado. Chamaremos isso de x.
O lado maior será igual a x√3.
Sua hipotenusa será igual a 2x.
A área é A = x²√3/2.
Por fim, o perímetro é P = x(3 + √3).

Quais são os dois triângulos especiais em trigonometria?

O triângulo 30° 60° 90° e o triângulo 45° 45° 90° (ou triângulo retângulo isósceles) são os dois triângulos especiais em trigonometria. Embora existam mais de dois triângulos retângulos especiais diferentes, esses são os mais reconhecidos e os mais fáceis de trabalhar. Um exemplo de triângulo retângulo especial não baseado em ângulo é um triângulo retângulo cujos lados formam um terno pitagórico.

3, 4 e 5 é um terno pitagórico?

Sim. Os números inteiros a = 3, b = 4 e c = 5 formam um terno pitagórico, pois a² + b² = c² e um triângulo com lados abc é um triângulo retângulo especial.

Triângulo retângulo especial

a

b

c

Perímetro

Área

Check out 19 similar triangle calculators 🔺

30 60 90 triangle45 45 90 triangleArea of a right triangle...16 more