Calculadora de Triângulo Retângulo

A calculadora de triângulo retângulo da Omni ajudará você a encontrar os comprimentos dos lados de um triângulo retângulo. Esta ferramenta também ensinará a você como encontrar a área de um triângulo retângulo, além de fornecer muitas informações sobre os usos práticos desse tipo de triângulo. Por exemplo, você já percebeu que um triângulo retângulo representa uma rampa com inclinação?

Neste artigo abordamos os chamados triângulos especiais, como, por exemplo, o triângulo 45 45 90, o triângulo 30 60 90 e o triângulo 3 4 5.

Discutiremos em detalhes:

• O que é um triângulo retângulo;
• Qual a área do triângulo abc;
• Triângulos especiais; e
• O que é um terno pitagórico.

Antes de mostrar como usar esta ferramenta para calcular triângulo retângulo online, vamos explicar o que é um triângulo retângulo. A definição é muito simples e pode até parecer óbvia para aqueles que já a conhecem: um triângulo retângulo é um triângulo em que um e somente um dos ângulos é exatamente 90°. Os outros dois ângulos serão claramente menores que o ângulo reto porque a soma de todos os ângulos em um triângulo é sempre 180°.

Em um triângulo retângulo, definimos os lados de uma maneira especial. O lado oposto ao ângulo reto é sempre o maior do triângulo e recebe o nome de "hipotenusa". Os outros dois lados são chamados de catetos. A relação entre a hipotenusa e cada cateto é direta, como veremos quando falarmos sobre o teorema de Pitágoras.

Nos exercícios envolvendo triângulos retângulos, em geral, há sempre uma incógnita a ser determinada, geralmente denominada como "x". Mostraremos a você como calcular o valor de x no triângulo retângulo. Além disso, com os conhecimentos adquiridos neste artigo, será muito fácil para você responder a pergunta: "qual a área do triângulo abc?".

Se tudo o que você deseja calcular é a hipotenusa de um triângulo retângulo, esta página e sua calculadora de triângulo retângulo funcionarão muito bem. No entanto, também recomendamos que você use a ferramenta que desenvolvemos na Omni, dedicada apenas a esse assunto, a calculadora de hipotenusa. A hipotenusa é o oposto do ângulo reto e pode ser resolvida usando o teorema de Pitágoras. Em um triângulo retângulo com catetos a e b e com hipotenusa c, o teorema de Pitágoras afirma que: a² + b² = c².

Para resolver c, tire a raiz quadrada de ambos os lados para obter c = √(b²+a²). Podemos considerar essa extensão do teorema de Pitágoras como uma "fórmula da hipotenusa". A calculadora do teorema de Pitágoras da Omni também é uma excelente ferramenta para calcular a hipotenusa.

Agora, vamos resolver um exemplo prático do que seria necessário para calcular a hipotenusa de um triângulo retângulo sem usar nenhuma calculadora disponível na Omni:

1. Obtenha os valores de a e b.
2. Eleve a e b ao quadrado.
3. Some os dois valores: a² + b².
4. Tire a raiz quadrada do resultado.
5. A raiz quadrada produzirá apenas resultados positivos, já que estamos lidando com comprimento.
6. O valor resultante é o valor da hipotenusa c.

Agora vamos ver como seria o processo usando uma das calculadoras da Omni, por exemplo, esta calculadora de triângulo retângulo:

1. Insira o valor de a e b na calculadora; e
2. Obtenha o valor de c imediatamente;
3. Como bônus, você ainda obterá o valor da área desse triângulo.

Você também quer saber como calcular o cateto adjacente? Para isso, você precisa do cateto oposto e da hipotenusa, ou então do cateto oposto e da área. O cateto adjacente será aquele que fica ao lado de um dos ângulos agudos do triângulo. Já o lado oposto ao ângulo agudo escolhido é o cateto oposto. Utilize nossa calculadora de triângulo retângulo e veja como é fácil determinar o cateto adjacente com esses dados.

Você quer saber qual a área do triângulo abc? Então, você está no lugar certo. Já vimos que calcular a área de um triângulo retângulo é muito fácil com a calculadora de triângulo retângulo. Na Omni, temos também uma calculadora projetada especificamente para essa finalidade, a calculadora da área de um triângulo retângulo. Vamos agora ver um pouco mais detalhadamente como calcular áreas de triângulos retângulos.

O método para encontrar a área de um triângulo retângulo é bem simples. Tudo o que você precisa saber são os comprimentos da base e da altura. Em um triângulo retângulo abc, onde "a" e "b" são catetos e "c" a hipotenusa, utilizaremos apenas os lados "a" e "b" para o cálculo da área, pois eles formam o ângulo reto do triângulo. Como a multiplicação desses dois valores juntos daria a área do retângulo correspondente, e o triângulo é a metade disso, a fórmula é

área = ½ × base × altura.

Se você não souber a base ou a altura, poderá encontrá-las usando o teorema de Pitágoras. Experimente a calculadora de triângulo retângulo para verificar seus cálculos ou calcular a área de triângulos com lados que tenham comprimentos maiores ou com valores decimais.

Agora, veremos outros parâmetros que podem ser calculados a partir de um triângulo retângulo usando algumas das ferramentas disponíveis na Omni. Note que um triângulo retângulo representa uma rampa com inclinação. Como sabemos a fórmula para a inclinação é

Inclinação = (y₂ - y₁)/(x₂ - x₁).

Portanto, se as coordenadas são (1,-6) e (4,8), a inclinação do segmento é (8 + 6)/(4 - 1) = 14/3. Uma maneira fácil de determinar se o triângulo é retângulo, e você sabe apenas suas coordenadas, é ver se as inclinações de quaisquer duas linhas se multiplicam resultando em -1.

Há uma maneira fácil de converter ângulos de radianos para graus e de graus para radianos com o uso da conversão de ângulos:

• Se um ângulo estiver em radianos, multiplique por 180/π; e
• Se um ângulo estiver em graus, multiplique por π/180.

Às vezes, você pode encontrar um problema em que faltam dois ou até três comprimentos de lados. Nesses casos, a calculadora de triângulo retângulo, a calculadora de hipotenusa e a calculadora da área de um triângulo retângulo não ajudarão você. Será necessário usar as funções trigonométricas para obter os dados que faltam.

O triângulo retângulo é apenas um dos muitos triângulos especiais que existem. Esses triângulos têm uma ou várias características especiais que os tornam únicos. Por exemplo, como vimos, o triângulo retângulo tem um ângulo reto e, portanto, uma hipotenusa, o que o torna um tipo único de triângulo. Além do triângulo retângulo, há outros triângulos especiais com propriedades interessantes.

Um dos triângulos especiais mais conhecidos é o triângulo equilátero, que possui seus três lados iguais e todos os seus ângulos têm 60°. Isso torna muito mais simples fazer com que uma calculadora de solução de triângulos avalie diferentes parâmetros desse triângulo.

Outro triângulo especial é o triângulo isósceles, que possui dois lados com comprimentos iguais e, portanto, dois ângulos do mesmo tamanho. Ao contrário do triângulo equilátero, os triângulos isósceles têm muitas formas diferentes.

Há muitos outros triângulos especiais. No entanto, agora veremos alguns triângulos retângulos especiais, isto é, além de serem triângulos retângulos, têm outras propriedades exclusivas que os tornam interessantes.

O triângulo a seguir é conhecido como triângulo "45 45 90", e é provavelmente o mais especial entre todos os triângulos retângulos especiais. Trata-se de um triângulo retângulo que também é um triângulo isósceles. Ambos os catetos têm o mesmo comprimento (isósceles), e ele também tem a peculiaridade que os ângulos não retos possuem exatamente a metade do tamanho do ângulo reto, o qual dá nome ao triângulo retângulo.

Esse triângulo retângulo é o tipo de triângulo que você pode obter quando divide um quadrado por sua diagonal. É por isso que os dois catetos (lados do quadrado) têm o mesmo comprimento. Para os interessados em saber mais sobre o mais especial dos triângulos retângulos especiais, recomendamos que você consulte a calculadora de triângulos 45 45 90 criada pela Omni para essa finalidade.

Outro fascinante triângulo do grupo de triângulos retângulos especiais é o chamado triângulo "30 60 90". O nome vem do fato de você ter um ângulo reto (90°), depois um ângulo de 30° e outro de 60°. Esses ângulos são especiais devido aos valores de suas funções trigonométricas (cosseno, seno, tangente, etc.). As consequências disso podem ser vistas e compreendidas com a calculadora de triângulos 30 60 90, mas para aqueles que têm preguiça de clicar no link, resumiremos algumas delas aqui. Supondo que o lado mais curto tenha comprimento a, os parâmetros do triângulo são:

1. O segundo comprimento é igual a a√3;
2. A hipotenusa é igual a 2a;
3. A área é igual a a²√(3/2); e
4. O perímetro é igual a a(3 + √3).

Há ainda, o chamado triângulo 3 4 5. Esse tipo de triângulo retângulo tem catetos iguais a 3 e 4 e sua hipotenusa vale 5. Ele é considerado um triângulo especial porque sua hipotenusa é obtida a partir de um quadrado perfeito. O triângulo 3 4 5 é o mais famoso triângulo Pitagórico, ou seja, um triângulo retângulo onde todos os lados possuem valores inteiros.

À primeira vista, pode parecer que um triângulo retângulo e um paralelogramo não têm nada em comum. Como um solucionador de triângulos pode ajudar você a entender um paralelogramo? A realidade é que qualquer paralelogramo pode ser decomposto em 2 ou mais triângulos retângulos. Vamos dar o exemplo do retângulo, que é o mais fácil de ver.

Imagine um retângulo qualquer. Agora desenhe um traço em uma das diagonais desse retângulo. Se separarmos o retângulo pela diagonal, obteremos dois triângulos retângulos. Observando os triângulos, não é necessário usar a calculadora de triângulos retângulos para ver que ambos são iguais, portanto, suas áreas serão as mesmas. Isso significa que a área do retângulo é o dobro da área de cada triângulo.

Se pensarmos nas equações, isso faz sentido, pois a área de um retângulo de lados a e b é exatamente área = a × b, enquanto a área do triângulo retângulo é área = base × altura / 2, o que, nesse caso, significaria área = a × b /2. Isso é exatamente o que já vimos quando cortamos o retângulo pela diagonal.

Esse foi um exemplo simples de um retângulo, mas o mesmo se aplica à área de um quadrado. Para outros paralelogramos, o processo se torna um pouco mais complicado (pode envolver até 4 triângulos retângulos de tamanhos diferentes). Ainda assim, com um pouco de habilidade, você pode usar a mesma ideia e calcular a área de um paralelogramo usando triângulos retângulos. Você pode, é claro, ser ainda mais eficiente e usar apenas a nossa calculadora.

A geometria e os polígonos, especialmente os triângulos, sempre aparecem juntos. As propriedades de alguns triângulos, como os triângulos retângulos, geralmente são interessantes, mesmo para quem não é matemático. Vamos agora dar uma olhada em um interessante conjunto de números intimamente relacionado a triângulos retângulos que os matemáticos adoram, e talvez você também goste.

Esses conjuntos de números são chamados de ternos pitagóricos e são conjuntos de 3 números inteiros (vamos chamá-los de a, b e c) que satisfazem o teorema de Pitágoras: a² + b² = c². Assim, um terno pitagórico, pode formar um triângulo retângulo com lados de comprimento a, b e c. Isso ocorre, por exemplo, no triângulo 3 4 5. A quantidade de números que satisfazem essa relação é limitada, mas os matemáticos têm prazer em procurar novos números.

Além do fator de curiosidade dessa relação, ela tem algumas propriedades interessantes que são exploradas na criptografia. Dadas as aplicações que podem ser encontradas para esses conjuntos de números, os matemáticos exploraram ainda mais, usando 4, 5... e mais conjuntos de números que satisfazem uma relação semelhante na qual a soma dos quadrados de todos os números, exceto um, dá o quadrado do número restante.

Também muito ligado a esses ternos pitagóricos está o último teorema de Fermat, no qual o quase lendário matemático enigmático Pierre Fermat afirmou que não poderia haver um conjunto de três números inteiros que satisfizesse a relação: aⁿ + bⁿ = cⁿ para n maior que 2. Essa conjectura ainda não foi provada matematicamente e é considerada um dos problemas matemáticos mais importantes até hoje.

Falamos muito sobre triângulos, especialmente triângulos retângulos, e suas aplicações em matemática e geometria. O que ainda não falamos é sobre a utilidade dos triângulos retângulos em situações da vida real. Pode parecer que as aplicações fora da geometria são limitadas, mas vamos dar uma olhada em um exemplo: nas sombras!

Sim, sombras. A sombra escura projetada por um objeto quando ele é iluminado. Se você observar a forma estabelecida pela sombra, pelo objeto e pelo chão, perceberá que ela é, na verdade, um triângulo retângulo! Pelo menos é assim quando o objeto está perfeitamente vertical e o chão está na horizontal. Na maioria das vezes, esse é o caso, ou pelo menos próximo disso. Isso significa que podemos usar a calculadora de triângulo retângulo para encontrar diferentes informações sobre objetos sob o sol. Vamos ver como.

Imagine que você tenha um prédio no qual queremos saber a altura, mas você não pode medi-lo diretamente porque é muito alto para deixar cair uma fita métrica do topo. O que você pode fazer é medir o comprimento da sombra na rua. Em seguida, com a ajuda de qualquer ferramenta de medição de ângulo e um pedaço de papel, você pode descobrir o ângulo entre a sombra e o chão. Sabendo que o ângulo entre o prédio e o chão é de 90°, você pode obter a altura do prédio.

Usando essa técnica, você pode medir a altura de muitos objetos, desde que tenha um dia ensolarado ou outras fontes de luz para iluminar o objeto. Na verdade, essa era uma técnica de medição muito comum antigamente. Provavelmente, o uso mais interessante e surpreendente dos triângulos retângulos é o de Eratóstenes, que conseguiu usar triângulos retângulos e sombras para medir o raio da Terra, e agora vamos explicar como ele fez isso.

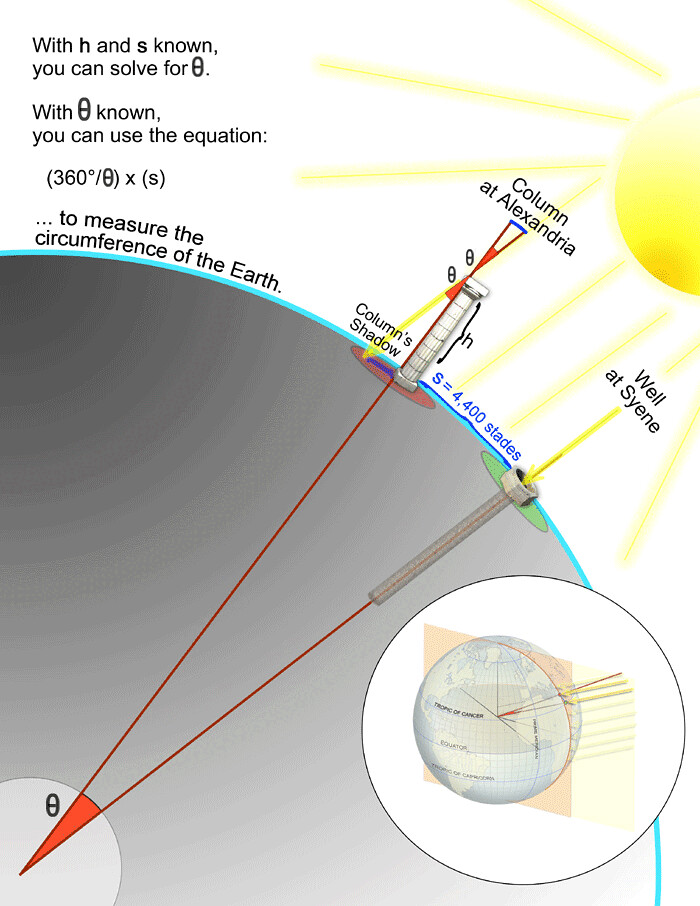
Eratóstenes notou que no solstício de verão havia um lugar na Terra onde os poços não tinham sombra ao meio-dia, ou seja, o sol brilhava diretamente sobre eles. Observando isso, ele montou uma coluna de altura conhecida a uma distância conhecida desse poço e mediu o tamanho da sombra criada pelo poste ao meio-dia no dia do solstício. Em seguida, usando triângulos retângulos e trigonometria, ele conseguiu determinar o ângulo indo do centro da Terra entre o poço e o poste, bem como o raio da Terra, com base na distância conhecida entre esses dois pontos.

Foi um feito surpreendente que agora você pode fazer com muito mais facilidade, usando apenas as calculadoras Omni que criamos para você.