Calculadora de Círculo

A calculadora de círculo da Omni ajudará você a determinar a circunferência, o diâmetro, a área e o raio de qualquer círculo.

No artigo abaixo, você encontrará todas as fórmulas de círculo que precisará para calcular esses parâmetros. Continue lendo se você estiver procurando a definição de círculo ou quiser entender como encontrar o centro de um círculo, a circunferência de um círculo, ou quiser saber mais sobre o que é pi.

Além disso, você encontrará informações abaixo sobre o círculo trigonométrico e as propriedades de um círculo, incluindo alguns fatos divertidos sobre essa forma. Se você quiser saber qual é o país mais redondo do mundo, continue lendo!

Neste artigo usaremos a seguinte notação:

• c para circunferência;
• d para diâmetro;
• a para área, e
• r para o raio do círculo.

Você prefere assistir ao invés de ler? Aprenda tudo o que precisa em 90 segundos com este vídeo que fizemos para você:

Um círculo é uma curva fechada e plana formada por todos os pontos que estão a uma determinada distância de um ponto em específico: o centro. Como alternativa, você pode definir o círculo como o locus de todos os pontos que estão à mesma distância de um determinado ponto fixo. O nome círculo deriva do grego, significando aro ou anel.

O círculo, tecnicamente falando, é apenas o limite, não a área dentro da forma. A figura inteira é chamada de disco. Um disco pode ser fechado se contiver o círculo que constitui seu limite e aberto se não o contiver. No dia à dia, o círculo às vezes é entendido como o disco, a superfície plana delimitada por essa curva.

O círculo pode ser definido pelos seguintes parâmetros:

• Circunferência: a distância ao redor da círculo;
• Raio: segmento de reta que une o centro do círculo a qualquer ponto da circunferência;
• Diâmetro: segmento de reta cujos pontos finais estão na circunferência e que passa pelo centro do círculo; e
• Corda: um segmento de reta cujos pontos finais estão na circunferência.

Há muitos outros termos associados ao círculo, como arco, secante ou tangente, mas, para nossas explicações básicas, você precisa entender apenas os descritos acima.

Um círculo é uma forma simples e distinta com muitas propriedades incomuns:

• Ele tem a maior área para um determinado comprimento de perímetro;
• Ele é altamente simétrico. A simetria de reflexão ocorre para todas as retas que passam pelo centro, enquanto a simetria radial ocorre para todos os ângulos; e
• Ele pode ser construído através de quaisquer três pontos no plano (nem todos na mesma reta).

Todos os círculos são semelhantes. Os círculos formados a partir de três pontos, por exemplo, com a ajuda de um triângulo, podem ser inscritos e circunscritos. Além disso, um círculo tem dezenas de outras propriedades interessantes, que você pode descobrir a seguir.

As equações mais populares associadas ao círculo são:

1. Área do círculo

   a = π · r²

2. Circunferência do círculo

   c = 2 · π · r

3. Diâmetro do círculo

   d = 2 · r

Você pode derivar muitas outras fórmulas a partir das equações acima, algo que exploraremos mais nos parágrafos abaixo.

Se você estiver procurando a fórmula do círculo em si, confira esta calculadora da equação de um círculo 🇺🇸.

O círculo trigonométrico, também conhecido como círculo unitário, é um círculo com raio igual a um. Normalmente, o seu centro é posicionado na origem (0, 0) no sistema de coordenadas cartesianas.

Vamos escolher qualquer ponto (x, y) no círculo trigonométrico. Então, |x| e |y| são os comprimentos dos lados do triângulo retângulo, com o raio do nosso círculo sendo a hipotenusa de comprimento 1. Usando o teorema de Pitágoras, podemos descobrir que:

x² + y² = 1

Como x² = (-x)², a equação acima funciona para todos os quadrantes, não apenas para o primeiro.

Além disso, podemos definir os lados do triângulo retângulo em termos de seno e cosseno:

cos(α) = x / 1 = x

sen(α) = y / 1 = y

Então:

sen²(α) + cos²(α) = 1

Essa equação é conhecida como a identidade trigonométrica fundamental. Para transformar tensões, você pode aplicá-la em círculos de Mohr, como pode ser verificado na calculadora de círculo de Mohr 🇺🇸 da Omni.

c é a circunferência do círculo, ou seja, o comprimento total da reta que você desenha com um compasso. Você pode calculá-la das seguintes maneiras:

1. Se você souber o raio ou o diâmetro do círculo:

   c = 2 · π · r = π · d

2. Se o raio e o diâmetro forem desconhecidos, então:

   c = 2√(π · a)

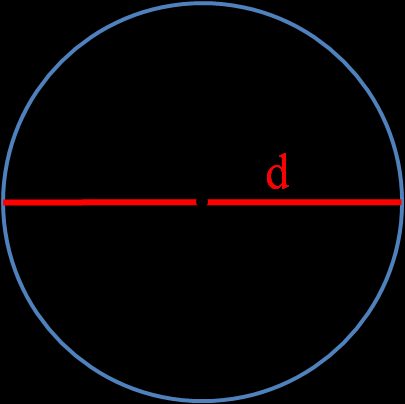
d é o diâmetro de um círculo, o comprimento de uma reta que passa pelo ponto central e une dois pontos do círculo. Você pode determiná-lo com estas equações:

1. Se você souber o raio do círculo:

   d = 2 · r

2. Se você não conhece o raio e a área:

   d = c / π

3. Se você não conhece o raio e a circunferência:

   d = 2√(a / π)

a representa a área do círculo. Esse é o único valor expresso em unidades quadradas (por exemplo, cm²). Você pode calculá-la da seguinte forma:

1. Se você conhece o raio ou o diâmetro do círculo, a fórmula da área do círculo é:

   a = π · r² = π · (d / 2)²

2. Se o raio e o diâmetro forem desconhecidos, você pode calculá-la a partir da circunferência:

   a = c² / 4π

Se você estiver interessado em cálculos que envolvam a fração de um círculo, verifique estas outras calculadoras da Omni:

• Calculadora da área de um semicírculo: desenvolvida específicamente para encontrar a área de meio círculo;
• Calculadora da área do setor circular: para verificar a área de uma fatia de pizza; ou
• Calculadora da área de um segmento: para determinar a área da seção transversal de um tubo parcialmente cheio.

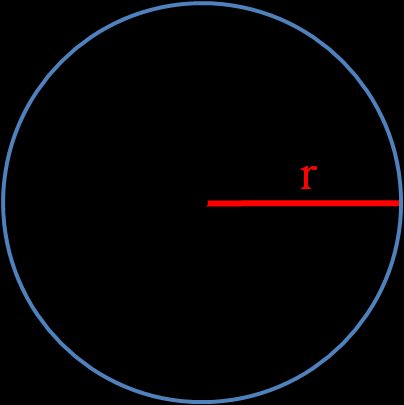
r, ou o raio do círculo, é o comprimento de uma reta que une o ponto central a qualquer ponto do círculo. Você pode encontrá-lo com as seguintes fórmulas:

1. Se você souber o diâmetro do círculo:

   r = d / 2

2. Se você não conhece o diâmetro e a área:

   r = c / 2·π

3. Se você não souber o diâmetro e a circunferência:

   r = √(a / π)

Há muitas maneiras de encontrar o centro de um círculo. Aqui mostraremos a você os dois métodos principais:

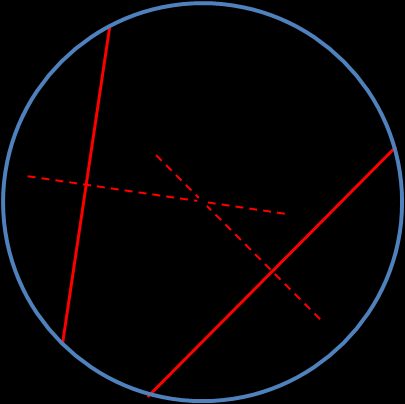
O método 1 é uma técnica simples para encontrar o centro de um círculo usando um compasso e uma régua:

1. Usando um compasso ou uma régua, desenhe duas cordas quaisquer.

2. Construa as bissetrizes perpendiculares de uma das cordas. Use um compasso para desenhar dois círculos sobrepostos (seus centros nos pontos finais das cordas, com o mesmo raio). Os círculos se cruzarão em dois pontos, desenhe uma reta através deles usando uma régua.

3. Repita o procedimento da bissetriz, definindo no segundo passo, para a segunda corda.

4. Duas bissetrizes se cruzarão em um ponto; esse é o centro do círculo.

Se quiser, você pode desenhar uma terceira corda, acompanhada de sua bissetriz, para aumentar (e verificar) a precisão da determinação do centro do círculo.

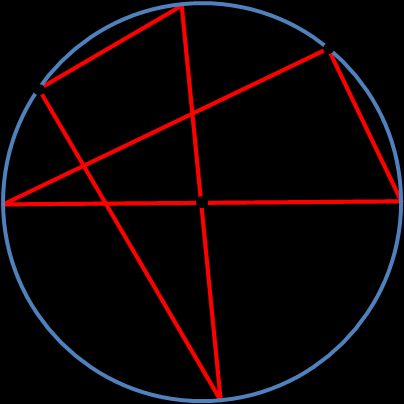
O método 2 é apenas uma estimativa aproximada do centro de um círculo, mas se você não precisar de grande precisão, poderá usar essa técnica:

1. Escolha um ponto no círculo.

2. Pegue algo que tenha um ângulo de 90 graus e bordas retas. Pode ser um esquadro, mas também qualquer coisa que você tenha à mão. Por exemplo, um livro, papelão ou uma folha de papel. Coloque o triângulo de tal forma que o ângulo retângulo esteja tocando o ponto escolhido.

3. Desenhe duas linhas perpendiculares ao círculo. Marque os pontos em que elas se cruzam com o círculo.

4. Desenhe linhas retas que passem pelos pontos. Esse é o diâmetro do círculo.

5. Você pode encontrar o centro de um círculo:

   • Construindo a bissetriz do diâmetro (como no primeiro método); ou
   • Simplesmente repetindo o procedimento: escolhendo outro ponto no círculo, desenhando linhas perpendiculares e criando outro diâmetro. A interseção de dois diâmetros nos mostrará o centro do círculo.

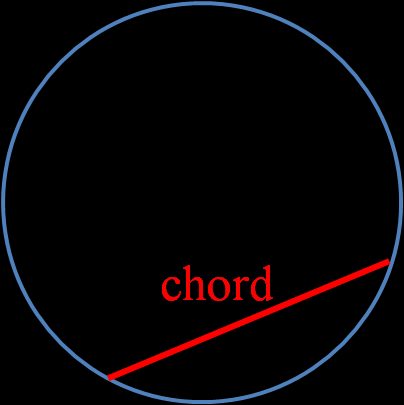
Uma corda é um segmento de reta que une dois pontos em qualquer curva. Essa curva pode ser um círculo, mas também, por exemplo, uma elipse. Se uma corda de um círculo passa pelo centro do círculo, ela é chamada de diâmetro e é a corda mais longa possível.

A corda de um círculo era amplamente usada na trigonometria antiga. Mesmo que a tenhamos substituído por funções trigonométricas, especialmente o seno, ainda é bom que você saiba como calcular seu comprimento em um círculo trigonométrico:

corda(α) = √[(1 - cos(α))² + sen²(α)] = √[2 - 2cos(α)] = 2sen(α/2)

onde α é um ângulo central, pego no sentido positivo, e deve estar no intervalo 0 < α ≤ π.

Você também pode encontrar o comprimento da corda de qualquer círculo multiplicando o valor da corda do círculo trigonométrico pelo raio do círculo, r, conforme mostrado na equação abaixo:

corda(α) = r × 2sin(α/2)

Os círculos concêntricos são círculos com um centro comum. O objeto em forma de anel, a região delimitada por dois círculos concêntricos de raios diferentes, é chamado de ânulo, mais conhecido como coroa circular.

São exemplos de círculos concêntricos na vida real:

• O alvo no arco e flecha ou o alvo de dardos.
• Ondulações circulares na água.
• Anéis de crescimento nas árvores (aproximadamente).
• Ranhuras em um disco de vinil ou CD.

Pi é a constante matemática mais conhecida. É a razão entre a circunferência de um círculo e seu diâmetro:

π = circunferência / diâmetro

Independentemente do tamanho do círculo, a razão c/d é constante. Normalmente, a constante pi é aproximada a alguns dígitos, por exemplo, quatro ou seis. Os primeiros 40 dígitos decimais são:

π ≈ 3.1415926535897932384626433832795028841971...

O π é um número irracional, o que significa que nenhum número finito de dígitos pode representar o π exatamente (e eles nunca se repetem). O número pi foi calculado com mais de vinte e dois trilhões de dígitos além de seu ponto decimal, e esse número ainda está aumentando com o desenvolvimento da tecnologia de computação.

Há competições em que os participantes tentam memorizar o maior número possível de dígitos de pi. O recorde mundial certificado pelo Guinness World Records é de 70.000 dígitos, enquanto um engenheiro japonês aposentado detém um recorde não oficial de mais de 100.000 dígitos.

Você sabia que..

• Existe um estilo de escrita chamado pilish. O comprimento das palavras consecutivas corresponde aos dígitos do pi. Por exemplo:

  • Ser o gato é minha obrigação de várias vidas seria 314159265 em pilish. Nove dígitos são muito mais fáceis de memorizar do que os 100.000 dígitos!; e

  Esse é um excelente método para você memorizar os dígitos do pi, pois o cérebro é muito melhor para lembrar palavras do que grandes sequências de números. Talvez você exercite sua mente e invente sua própria história em pi?

• Vários livros sobre a constante pi foram publicados. Há, é claro, ensaios matemáticos padrão entre eles, mas isso não é tudo. Se procurar bem, econtrará até mesmo livros completos escritos em pilish! O livro chamado "Not A Wake: A Dream Embodying π's Digits Fully for 10000 Decimals", de Mike Keith, detém o recorde do mais longo texto em pilish, com 10.000 dígitos.

• Há um Dia do Pi comemorado por muitos entusiastas do π. É em 14 de março, como a data sugere (3/14). Há alguns anos, em 2015, houve um dia "especial" do Pi, pois os próximos dois dígitos apareceram na data (3/14/15). E a hora (9:26:53) adicionou ainda mais dígitos!

• Embora aprender π com centenas ou milhares de dígitos possa ser divertido (?), foi determinado que apenas 38 casas decimais são suficientes para medir a circunferência do Universo observável, com a precisão da largura de um átomo de hidrogênio. Confira o vídeo sobre π e o tamanho do Universo feito pelo matemático James Grime no canal do Numberphile.

No uso cotidiano, elevar o círculo ao quadrado é uma metáfora para você se esforçar em tarefas difíceis ou até mesmo impossíveis. Mas o que isso significa do ponto de vista matemático?

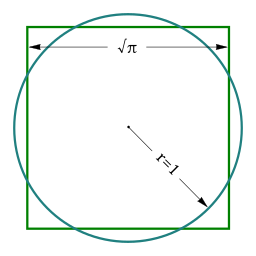
Esse tem sido um problema para os matemáticos desde a antiguidade. É a tarefa de construir um quadrado igual em área a um círculo, mas usando apenas uma régua e um compasso. A solução do problema foi provada impossível em 1882, quando o matemático Lindemann mostrou que π é um número transcendental; portanto, π e √π não podem ser construídos. No entanto, se removermos a restrição da régua e do compasso, o problema é fácil e já foi resolvido e descrito muitas vezes.

Você pode encontrar a combinação de palavras quadrado e círculo na vida cotidiana: os ringues de boxe e de luta livre são conhecidos como círculos quadrados. O nome vem do formato tradicional de um ringue.

Um círculo é uma forma 2D que serve como base em algumas formas geométricas curvilíneas 3D.

Um cilindro tem duas bases paralelas (geralmente circulares). Além disso, a única base de um cone é, na maioria das vezes, um círculo.

Como conhecemos a fórmula da área de um círculo, podemos calcular facilmente os volumes dessas formas:

v(cilindro) = π · r² · h

v(cone) = π · r² · h/3

Quando se trata de uma esfera, ela é um objeto 3D definido como somente a superfície de uma bola completamente redonda. É algo análogo ao círculo e ao disco, mas em três dimensões ao invés de duas.

Um círculo máximo é aquele cujo plano passa pelo centro da esfera; qualquer outro é chamado de círculo menor. Ele é usado, por exemplo, em cartografia e geografia. O equador é o único círculo máximo na família dos paralelos de latitude. No entanto, todos os meridianos de longitude, emparelhados com seu meridiano oposto, formam círculos máximos.

Podemos comparar países de várias maneiras: por sua área, população ou PIB, mas você já se perguntou qual é o país mais redondo do mundo?

Um matemático e blogueiro, Gonzalo Ciruelos, calculou o parâmetro de redondeza e criou a classificação. O vencedor na categoria de redondeza é Serra Leoa, enquanto o título de país menos redondo do mundo vai para as Ilhas Marshall.

Serra Leoa é o primeiro país em redondeza, mas também é o 14º em outra classificação: o país mais retangular do mundo! Para deixar tudo ainda mais confuso, o 4º país mais redondo (Cidade do Vaticano) é o 2º país mais retangular do mundo, e a Polônia, 5ª na classificação de redondeza, é a 10ª na classificação de retangularidade. Como é possível ser retangular e redondo ao mesmo tempo?!

É tudo uma questão de definição de retangularidade e circularidade, que pode não ser adequada para formas complexas ou dispersas, e as fronteiras das nações geralmente são.

Você pode encontrar uma explicação melhor e uma discussão dos resultados no site do bigthink.

Se você ainda não tem certeza de como usar nossa calculadora de círculo, dê uma olhada nesta ilustração:

1. Suponha que você queira calcular o tamanho de um agroglifo. Escolheremos aquele inspirado na identidade de Euler, encontrado em 2010 em Wilton, perto de Marlborough, Reino Unido. A identidade de Euler é um caso especial da fórmula de Euler (que pode ser derivada do círculo trigonométrico no plano complexo).

2. Digite a dimensão fornecida na calculadora de círculo. Sabemos que o círculo da plantação tinha aproximadamente 90 metros de diâmetro. Se você precisar alterar as unidades, clique no nome da unidade e escolha a que você precisa em uma lista suspensa (metros, no nosso caso).

3. Pronto! Graças a essa ferramenta incrível, você descobriu todos os parâmetros do círculo num piscar de olhos! Agora sabemos que:

   • A circunferência do círculo é igual a 282,743 metros;
   • O raio é 45 metros; e
   • A área é de 6.361,7m². Quase a área de um campo de futebol! (para ser mais exato: ~92% da área de um campo de futebol).

Experimente a calculadora você mesmo. No tema de círculos, por que você não verifica qual é a circunferência da roda da sua bicicleta?

Normalmente, por C, denotamos o comprimento da circunferência de um círculo, que é a distância em torno de um círculo. Se você souber o raio, então C é igual a 2 π × raio.

Sim, para encontrar a circunferência a partir do diâmetro, você deve usar a fórmula C = π × diâmetro. Isso decorre do fato de que diâmetro = 2 × raio, que pode ser substituído pela famosa fórmula C = 2π × raio.

Para determinar a área de um círculo a partir de sua circunferência, siga os passos a seguir:

1. Eleve a circunferência ao quadrado, ou seja, compute c².
2. Divida o resultado por 4π.
3. Pronto! Acabamos de aplicar a fórmula a = c² / 4π, que relaciona a área de um círculo à sua circunferência.

A resposta é 2√π ≈ 3,54. Isso ocorre porque c² = 4π × área e, portanto, pegando a raiz quadrada e colocando área = 1, obtemos c = √(4π × 1) = 2√π ≈ 3,54.