Calculadora da Área do Setor Circular

Com esta calculadora de área de setor circular da Omni, você poderá rapidamente encontrar qualquer área de setor circular, por exemplo, a área de um semicírculo ou de um quadrante. Neste breve artigo, nós vamos:

• Fornecer uma definição de setor e explicar o que é um setor de um círculo.

• Mostrar a fórmula da área do setor e explicar como você mesmo pode derivar a equação sem muito esforço.

• Revelar alguns exemplos da vida real onde a calculadora de área de setor pode ser útil.

Então, vamos começar com a definição de setor: o que é um setor em geometria?

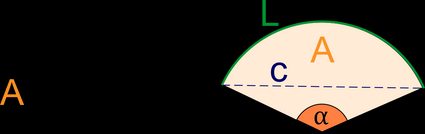
Um setor é uma região geométrica formada pela delimitação de um círculo por dois raios e o arco entre eles.

Os setores de um círculo são mais comumente visualizados em gráficos de pizza, nos quais um círculo é dividido em vários setores para mostrar o peso de cada segmento. As imagens abaixo mostram alguns exemplos de setores de círculos. Como você pode ver, nem sempre eles se parecem com uma fatia de torta, às vezes, eles se parecem mais com o que sobra da torta depois que você tira uma fatia:

Muito raramente você vai ouvir falar sobre o setor de uma elipse. Quando isso acontecer, tenha em mente que as fórmulas deste tipo de setor são muito mais difíceis de usar do que as equações da área do setor de um círculo.

A fórmula para a área do setor é simples: multiplique o ângulo central pelo raio ao quadrado e divida por 2:

• Área do setor = r² ⋅ α / 2

Mas de onde ela vem? Você pode encontrá-la usando proporções. Tudo o que você precisa lembrar é a fórmula da área do círculo (e temos certeza que você já sabe qual fórmula é essa!):

1. A área de um círculo é calculada como A = π ⋅ r². Esse é um ótimo ponto de partida.

2. O ângulo total é 2π em radianos ou 360° em graus, sendo que este último é a unidade angular mais comum.

3. Em seguida, queremos calcular a área de uma parte de um círculo, expressa pelo ângulo central.

   • Para ângulos de 2π (círculo completo), a área é igual a π⋅r²:

     2π → π ⋅ r²

   • Então, qual é a área do setor de um círculo?

     α → Área do setor

4. A partir da proporção, podemos encontrar facilmente a fórmula final da área do setor:

   Área do setor = α ⋅ π ⋅ r² / 2π = α ⋅ r² / 2

O mesmo método pode ser usado para encontrar o comprimento do arco; tudo o que você precisa lembrar é a fórmula para o perímetro de um círculo. Leia mais sobre isso na calculadora de circunferência e na calculadora de comprimento do arco da Omni.

Agora, encontrar a área de um semicírculo ou quadrante deve ser muito fácil. Basta você pensar em que parte de um círculo eles estão!

1. Área do semicírculo: π ⋅ r² / 2

• Sabendo que se trata da metade do círculo, divida a área por 2:

  Área do semicírculo = Área do círculo / 2 = π ⋅ r² / 2

• Obviamente, você obterá o mesmo resultado ao usar a fórmula da área do setor. Lembre-se apenas de que o ângulo reto é π (180°):

  Área do semicírculo = α ⋅ r² / 2 = π ⋅ r² / 2

2. Área do quadrante: π ⋅ r² / 4

• Como um quadrante é um quarto de um círculo, podemos escrever a fórmula como:

  Área do quadrante = área do círculo / 4 = π⋅r² / 4

• O ângulo central do quadrante é um ângulo reto (π/2 ou 90°), portanto, você chegará rapidamente à mesma equação:

  Área do quadrante = α ⋅ r² / 2 = π ⋅ r² / 4

Provavelmente, você está se perguntando: "por que precisamos aprender isso? Nunca vamos usar isso". Bem, gostaríamos de mostrar a você que a geometria está ao nosso redor:

• Se você está se perguntando qual o tamanho do bolo que deve pedir para a sua incrível festa de aniversário, acertou! É isso mesmo! Use a fórmula da área do setor para estimar o tamanho de uma fatia 🍰 para seus convidados, para que ninguém morra de fome.

• É uma história semelhante com a pizza. Você notou que cada fatia é um setor de um círculo 🍕? Por exemplo, se você não for um grande fã da borda, pode calcular qual tamanho de pizza será o melhor para você.

• Algum entusiasta da costura aqui? 👗 Os cálculos da área do setor podem ser úteis na preparação de uma saia circular (já que nem sempre é um círculo completo, e sim um setor de um círculo).

Além desses exemplos simples da vida real, a fórmula da área do setor pode ser útil em geometria, por exemplo, para encontrar a área da superfície de um cone. Saiba mais com a calculadora da área de superfície do cone da Omni.