Última atualização: 30 de Oct. de 2024

Calculadora de Deslocamento de Tubos 45

Q: Como encontrar o deslocamento de um tubo?

Para encontrar o deslocamento de um tubo: Meça o deslocamento horizontal, o deslocamento vertical e a distância horizontal do deslocamento . Eleve ao quadrado cada uma dessas medições e, em seguida, some todas elas . Pegue a raiz quadrada da soma para obter o deslocamento. Se você não souber o valor da distância horizontal ou tiver um ângulo de curvatura preferido para a conexão, repita os passos 2 e 3 com a distância horizontal igual a zero e divida tudo pelo seno do ângulo de curvatura da conexão.

Criada por Kenneth Alambra

Kenneth Alambra

Holds a Bachelor’s degree in Civil Engineering with 3+ years experience in fit-out construction and another 3+ years in technical sales. Ken has always been interested in creativity and innovation. He finds himself having fun solving problems and thinking of ways to improve anything he comes in contact with. During his free time, he plays a lot of bullet chess, listens to some pop music, or tries to learn something new – like preparing his favorite foods. See full profile

Check our editorial policy

Revisada por Dr.(a) Wojciech Sas

Wojciech Sas

PhD, Institute of Physics in Zagreb

A physicist at the Institute of Nuclear Physics in Kraków. Currently looking for that one and only magnetic nanomaterial that will improve everyone's life. Interested in astronomy and likes playing board games. Also, fond of watching chess tournaments; he never refuses to play a game (or two) himself. See full profile

Check our editorial policy

e Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

Traduzida por Doutorando(a), Marinara Andrade do Nascimento Moura

Marinara Andrade do Nascimento Moura

PhD candidate

LinkedInWebsiteResearch Gate

Marinara holds a master’s degree in Technology and is working on her PhD in Civil Engineering. She has always been interested in science and engineering, mostly because she is passionate about solving problems. She has published her articles in important scientific journals and international conferences as a researcher. She has experience teaching undergraduate students and believes that teaching is a perfect way to learn because the more we give, the more we have. In her free time, she loves to cook (and eat!), travel with her husband, and chat with her friends. See full profile

Check our editorial policy

e Dr.(a) João Rafael Lucio dos Santos

João Rafael Lucio dos Santos

PhD, Federal University of Campina Grande

LinkedInWebsiteResearch Gate

Joao is a physicist, researcher, and professor in Brazil. He earned his Ph.D. in Physics at the University of Rochester, NY in 2013. He has written several papers in international journals, mainly in field theory and cosmology. Joao is also a researcher and the outreach leader for the BINGO telescope. This state-of-the-art radio telescope will be operating in the Northeast of Brazil in a few years. He believes in the importance of spreading knowledge and high-quality information among society and the public in general. He also believes that people can enjoy the learning process if it is funny and if they can see it as a path to change their life, even in daily activities. In his free time, he enjoys running, playing tennis, cooking, traveling, and having pleasant moments with his relatives and friends. See full profile

Check our editorial policy

Novo

Índice

O que é o deslocamento de um tubo?Como usar a calculadora de deslocamento de tubo 45?Como calcular o deslocamento de um tubo?Como fazer um deslocamento de 45 graus de um tubo? Exemplo de cálculo Como calcular o deslocamento de uma tubulação de forma rápida? Com o uso de multiplicadores de deslocamento de tubulação Perguntas frequentes

A calculadora de deslocamento de tubos da Omni ajudará você a encontrar a distância necessária para completar um deslocamento de tubo necessário para qualquer curva típica de conexões de tubo ou qualquer ângulo de curva que você preferir.

Nesta calculadora, você aprenderá:

O que é deslocamento de tubo (rolling offset);
As diferentes fórmulas de deslocamento de tubo; e
Como calcular o rolling offset.

Você também aprenderá sobre os diferentes termos que normalmente usamos ao lidar com deslocamentos de tubos, como deslocamento vertical, deslocamento real e distância horizontal. Além disso, mostraremos um gráfico de deslocamento de tubo que contém multiplicadores de deslocamento de tubo que você pode usar para encontrar o comprimento do percurso de forma rápida e fácil.

O que é o deslocamento de um tubo?

Ao realizar alguns trabalhos com tubulações, às vezes nos deparamos com situações em que temos de conectar duas tubulações que não estão totalmente alinhadas entre si. Essas duas tubulações podem estar deslocadas horizontal ou verticalmente. Quando vemos uma combinação de deslocamento horizontal e vertical ou, em outras perspectivas, uma combinação de deslocamentos em duas direções diferentes, chamamos isso de deslocamento de tubulação.

Para lidar com deslocamentos de tubulação, podemos usar uma conexão de tubulação curvada para mudar a direção da tubulação e outra conexão curvada para retornar à direção final da tubulação. Nesta calculadora, abordamos como encontrar o comprimento do percurso (ou travel length, termo em inglês), que é o comprimento da diagonal que conecta os dois pontos em que a tubulação muda de direção, conforme mostrado na imagem abaixo:

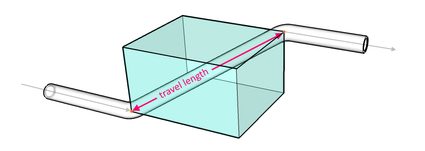
Diagrama simples de tubulação mostrando os dois pontos de curvatura diferentes de uma tubulação e o comprimento do deslocamento. — Ilustração do comprimento do percurso (*travel length*).

Você pode calcular o comprimento da tubulação usando trigonometria, alguns conceitos são baseados nos triângulos retângulos e no Teorema de Pitágoras (mais detalhes na calculadora do Teorema de Pitágoras). Antes de prosseguirmos com o cálculo, vamos primeiro aprender a usar a nossa calculadora de deslocamento de tubos.

Como usar a calculadora de deslocamento de tubo 45?

Usar nossa calculadora de deslocamento de tubos é fácil, pois você não precisa conhecer nenhuma fórmula para isso. Nossa ferramenta também pode ajudar você a visualizar a aparência do seu tubo com diagramas que mudam de acordo com a sua seleção e entradas. Aqui estão os passos que você pode seguir para usar a nossa calculadora:

Digite os deslocamentos horizontais e verticais necessários para sua tubulação. Nossa calculadora de deslocamento de tubos mostrará instantaneamente o deslocamento real da sua tubulação.
Em seguida, escolha a curvatura de conexão preferida, dependendo do que estiver disponível. Você pode personalizar de acordo com as suas necessidades, seja se você estiver dobrando o seu próprio tubo ou se tiver acessórios para tubos com curvatura de ângulo personalizada.
Se você escolher a opção de personalizar, nossa ferramenta exibirá o Ângulo de curvatura das conexões para que você possa entrar com o seu ângulo de curvatura desejado.
Ao selecionar ou inserir a curva do acessório, você verá o comprimento da tubulação e o comprimento da distância horizontal que a tubulação precisa seguir para completar o deslocamento.

Na próxima seção deste texto, você aprenderá a calcular os deslocamentos por conta própria para entender melhor como funciona a nossa calculadora.

Como calcular o deslocamento de um tubo?

Para calcular um deslocamento de um tubo 45, você precisa encontrar duas hipotenusas de dois triângulos retângulos dentro de uma caixa imaginária formada por uma tubulação. Temos a calculadora de hipotenusa e a calculadora de triângulo retângulo separadas se você quiser ir mais afundo nesses tópicos.

Na ilustração abaixo, podemos ver que é possível considerar as medições de deslocamento horizontal e vertical como os lados de um triângulo retângulo, e sua hipotenusa é o deslocamento real:

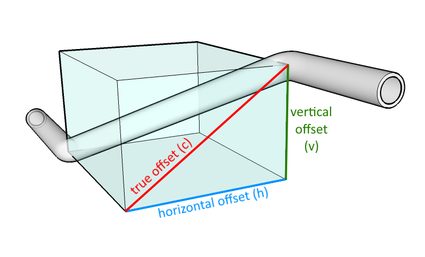
Imagem mostrando o primeiro triângulo retângulo, a distância horizontal, a distância vertical e o deslocamento real. — Primeiro triângulo retângulo formado por: deslocamento horizontal (horizontal offset), deslocamento vertical (vertical offset) e comprimento do percurso (travel length).

Usando o teorema de Pitágoras, podemos determinar o valor do deslocamento real (true offset) $c$ , que é simplesmente a diagonal de um retângulo, usando a seguinte equação:

c = \sqrt{h^2 + v^2}

onde:

$c$ : deslocamento real(true offset);
$h$ : deslocamento horizontal (horizontal offset); e
$v$ : deslocamento vertical (vertical offset).

Agora vamos dar uma olhada dentro da caixa imaginária para ver outro triângulo retângulo formado pelo true offset, travel length e o run, com a ajuda desta ilustração:

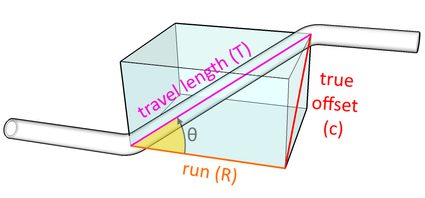
Imagem mostrando o segundo triângulo retângulo e a viagem como hipotenusa. — Segundo triângulo retângulo, formado pela distância horizontal (run), o comprimento do percurso (travel length) e o deslocamento real (true offset).

Nesse triângulo, não podemos usar o teorema de Pitágoras, pois inicialmente não sabemos o valor da distância horizontal $R$ , necessária para obter o comprimento do percurso $T$ . Entretanto, como sabemos o ângulo de curvatura da conexão do tubo que queremos usar, podemos utilizar a função trigonométrica seno (para mais detalhes, veja a calculadora de funções trigonométricas 🇺🇸) para obter o valor de $T$ , conforme a equação abaixo:

T = \frac{c}{\text{sen}(\theta)}

onde:

$T$ : comprimento do percurso (travel length) do tubo que conecta os dois cantos opostos da nossa caixa imaginária;
$c$ : deslocamento da tubulação; e
$\theta$ : ângulo de curvatura da conexão do tubo que você usará.

Você pode então usar o teorema de Pitágoras para encontrar o comprimento da distância horizontal usando essa equação:

R = \sqrt{T^2 - c^2}

ou a função trigonométrica de uma tangente, como mostrado aqui:

R = \frac{c}{\tan(\theta)}

Além dessas equações, também vale a pena observar que caso você já saiba o valor da distância horizontal, juntamente com os valores dos deslocamentos horizontal e vertical, você pode obter diretamente o valor de $T$ usando essa equação:

T = \sqrt{R^2 + h^2 + v^2}

Agora que você conhece todas as equações necessárias para calcular as medições de deslocamento de tubos 45, que tal seguirmos para um exemplo 🙂?

Como fazer um deslocamento de 45 graus de um tubo? Exemplo de cálculo

Digamos que você queira conectar dois tubos que estão deslocados horizontal e verticalmente em um metro (100 cm) e meio metro (50 cm), respectivamente. Nessa situação, planejamos usar cotovelos de 45 graus para completar o deslocamento. Então, como fazemos esse deslocamento de 45 graus? Podemos começar obtendo o deslocamento da tubulação usando nossa equação:

\begin{align*} c &= \sqrt{h^2 + v^2}\\[0.5em] &= \sqrt{100^2 + 50^2}\\[0.5em] &= \sqrt{10.000 + 2.500}\\[0.5em] &= \sqrt{12.500}\\[0.5em] &= 111{,}80\ \text{cm} \end{align*}

Então, usando nossa equação para encontrar o comprimento do percurso, temos:

\begin{align*} T &= \frac{c}{\text{sen}(\theta)}\\[1.2em] &= \frac{111{,}80\ \text{cm}}{\text{sen}(45\degree)}\\[1.2em] &= 158{,}11\ \text{cm} \end{align*}

Assim, você pode saber qual seria a distância horizontal usando uma das duas equações discutidas anteriormente. Neste exemplo, vamos tentar usar a equação com a função tangente da seguinte forma:

\begin{align*} R &= \frac{c}{\tan(\theta)}\\[1.2em] &= \frac{111{,}80\ \text{cm}}{\tan(45\degree)}\\[1.2em] &= 111{,}80\ \text{cm} \end{align*}

Agora, com os cálculos que fizemos, sabemos as distâncias necessárias para completar o deslocamento do nosso tubo. Além disso, observe que a distância horizontal é sempre igual ao deslocamento real sempre que usamos cotovelos de 45 graus. Para outros ângulos de conexões de tubulação, seus valores já serão diferentes.

💡 Lembre-se que você precisa ajustar o comprimento do percurso de acordo com as permissões da conexão para determinar o comprimento necessário do tubo a ser cortado para a montagem perfeita da tubulação.

Como calcular o deslocamento de uma tubulação de forma rápida? Com o uso de multiplicadores de deslocamento de tubulação

Outra maneira de determinar o comprimento do percurso é usar algumas constantes multiplicadoras de deslocamento de tubo. Essas constantes serão úteis, especialmente quando você quiser calcular os comprimentos de percurso por conta própria, mas tiver apenas uma calculadora que não tenha funções trigonométricas. Essas constantes estão na tabela de deslocamento de tubo abaixo para que você tenha uma referência:

Curva de ajuste	Multiplicador
22 ½°	2,6131
45°	1,4142
60°	1,1547
90°	1,0000

No entanto, para usar um multiplicador de deslocamento de tubo, primeiro você precisa avaliar o true offset. Em seguida, para encontrar o comprimento do percurso, você deve multiplicar a constante pelo true offset, conforme mostrado na equação abaixo:

T = m\cdot \sqrt{h^2 + v^2}

em que $m$ é o multiplicador de deslocamento do tubo.

✅ Se o cálculo de ângulos no mundo da construção lhe interessa tanto quanto os cálculos de deslocamento de tubos, talvez você também goste da nossa calculadora de corte angular 🇺🇸 e da nossa calculadora de ângulo de esquadria. 😊

Perguntas frequentes

O que é um deslocamento de tubo?

Quando precisamos deslocar uma tubulação nas direções horizontal e vertical, temos um deslocamento de tubo. Imagine uma tubulação que entra em um canto de uma caixa imaginária e sai no canto diagonal oposto mais distante da referida caixa imaginária. Você pode completar um deslocamento de tubo encontrando o que é chamado de comprimento de percurso do tubo.

Como calcular o deslocamento de tubulação?

Para calcular o deslocamento na tubulação:

Meça as distâncias horizontal e vertical do deslocamento.
Determine o deslocamento real, que é a hipotenusa do triângulo retângulo formado por esses deslocamentos.
Divida o true offset pelo seno do ângulo de curvatura da conexão para encontrar o comprimento do percurso.
Além disso, você pode dividir o true offset pela tangente do ângulo de curvatura da conexão para estimar a distância horizontal do deslocamento.

Como calcular um deslocamento de tubo 45?

Para calcular um deslocamento de tubo 45 usando conexões de 45 graus:

Determine os deslocamentos horizontal e vertical da sua tubulação.
Pegue a raiz quadrada da soma dos quadrados dos deslocamentos horizontal e vertical. Esse será o true offset do seu deslocamento.
Finalmente, multiplique o true offset por 1,4142 ou divida-o por sen(45°).

Como colar as conexões de tubos de PVC?

A melhor maneira de colar acessórios de PVC em tubos é usar cimento solvente de PVC. Os cimentos solventes de PVC derretem temporariamente as superfícies dos materiais de PVC em que você os aplica. Enquanto essas superfícies do PVC derretem, você pode colocá-las em contato umas com as outras para formar uma ligação química à medida que secam. Ao usar o cimento solvente para PVC, certifique-se de torcer um pouco o tubo e a conexão para garantir uma conexão adequadamente vedada.

Como encontrar o deslocamento de um tubo?

Para encontrar o deslocamento de um tubo:

Meça o deslocamento horizontal, o deslocamento vertical e a distância horizontal do deslocamento.
Eleve ao quadrado cada uma dessas medições e, em seguida, some todas elas.
Pegue a raiz quadrada da soma para obter o deslocamento.
Se você não souber o valor da distância horizontal ou tiver um ângulo de curvatura preferido para a conexão, repita os passos 2 e 3 com a distância horizontal igual a zero e divida tudo pelo seno do ângulo de curvatura da conexão.

Qual é o deslocamento 45 graus de um 1x1 m²?

Para encontrar o comprimento do percurso de deslocamento de um tubo com deslocamento horizontal de 1 m e distância vertical de 1 m usando uma conexão de 45 graus:

Eleve ao quadrado os deslocamentos horizontal e vertical e some-os da seguinte forma: 1² + 1² = 2.
Tire a sua raiz quadrada para encontrar o true offset: √2 = 1,41421 metros.
Finalmente, divida 1,41421 m pelo seno de 45° para obter 1,41421 m/sen (45°) = 2 m.