Kalkulator przedziału ufności

Omni kalkulator przedziałów ufności jest narzędziem, które pomoże ci wyznaczyć przedział ufności dla próbki, o ile podasz nam średnią 🇺🇸, odchylenie standardowe i wielkość próbki. Możesz ustalić dowolny poziom ufności. Jeśli chcesz dowiedzieć się, czym jest przedział ufności i jak go obliczamy lub też szukasz wzoru na 95% przedział ufności dla wartości z (z-score), poniższy artykuł z pewnością ci pomoże.

Formalna definicja mówi, że, „przedział ufności to uzyskany na podstawie próbki losowej zakres wartości parametru populacji, który z dużym prawdopodobieństwem zawiera prawdziwą wartość nieznanego parametru”. Ale co to oznacza w praktyce?

Wyobraźmy sobie, że producent cegieł martwi się, czy masa produkowanych przez niego cegieł jest zgodna ze specyfikacją. Wyznaczył, że średnia masa próbki 100 cegieł jest równa 3 kg. Stwierdził również, że 95% przedział ufności wynosi od 2,85 kg do 3,15 kg. Oznacza to, że może być w 95% pewien, że średnia masa wszystkich wyprodukowanych przez niego cegieł będzie się mieścić w przedziale od 2,85 kg do 3,15 kg. Mówiąc nieco precyzyjniej: jeśli producent będzie wielokrotnie losował próbki 100 cegieł i wyznaczał na podstawie każdej z nich przedział ufności, to 95% tych przedziałów będzie zawierało prawdziwą średnią masę cegły.

Oczywiście, nie zawsze chcemy mieć dokładnie 95% pewności — czasami potrzeba więcej, czasami wystarcza mniej. Być może chcesz mieć aż 99% pewności, a może wystarczy ci, że przedział ufności jest poprawny w 90% przypadków? Ten procent nazywa się poziomem ufności.

Obliczenie przedziału ufności wymaga znajomości trzech parametrów próby: wartości średniej, μ, odchylenia standardowego, σ, oraz liczebności próby, n (czyli liczby wykonanych pomiarów). Mając te dane, możemy wyznaczyć błąd standardowy 🇺🇸, a potem błąd statystyczny według następujących wzorów:

błąd standardowy = σ/√n

błąd statystyczny = błąd standardowy · Z(0,95)

gdzie Z(0,95) to wartość z odpowiadająca poziomowi ufności 95%. Jeśli używasz innego poziomu ufności, musisz obliczyć odpowiednią wartość z. Ale nie martw się, nasz kalkulator wartości z ułatwi ci to zadanie!

Jak znaleźć wartość Z(0,95)? Jest to taka liczba, która ma następującą własność — podczas losowania ze standardowego rozkładu normalnego z prawdopodobieństwem 95% uzyskamy wartość nie większą niż Z(0,95). Oznacza to, że jeśli narysujesz gęstość rozkładu normalnego 🇺🇸 N(0,1), to pole pod krzywą pomiędzy -Z(0,95) oraz Z(0,95) będzie równy 0,95. Przypomnijmy, że całe pole pod tą krzywą wynosi 1.

Jeśli chcesz obliczyć tę wartość korzystając z tabeli wartości z, to musisz:

1. Wybrać swój poziom ufności. Załóżmy, że jest to 95%.

2. Obliczyć, jakie jest prawdopodobieństwo, że twój wynik nie znajdzie się w przedziale ufności. Wartość ta jest równa 100% - 95% = 5%.

3. Przyjrzyj się gęstości rozkładu normalnego. 95% to obszar pomiędzy -Z(0,95) oraz Z(0,95). Oznacza to, że obszar na lewo od -Z(0,95) jest równy 0,025 (2,5%), zaś obszar na prawo od Z(0,95) jest również równy 0,025 (2,5%).

4. Obszar na prawo od Z(0,95) wyznacza też wartość p odpowiadającą twojej wartości z. Możemy użyć tabel, aby znaleźć wartość z odpowiadającą wartości p równej 0,025. Otrzymamy liczbę z równą 1,959.

Po obliczeniu wartości Z(0,95) możesz ją podstawić do podanego wyżej wzoru, aby uzyskać błąd statystyczny. Pozostaje nam tylko znaleźć dolny i górny koniec przedziału ufności:

dolny koniec = średnia - błąd statystyczny

górny koniec = średnia + błąd statystyczny

Aby obliczyć (dwustronny) przedział ufności, wykonaj następujące kroki:

1. Ustal wielkość próby. Załóżmy, że wynosi ona n = 100.

2. Znajdź średnią wartość swojej próbki. Przyjmijmy, że jest to 3.

3. Wyznacz odchylenie standardowe próby. Załóżmy, że wynosi ono σ = 0,5.

4. Wybierz poziom ufności. Najczęściej jest to 95%.

5. W tabeli statystycznej znajdź wartość Z(0,95), czyli 97,5 kwantyl rozkładu N(0,1). W naszym przykładzie będzie to 1,959.

6. Oblicz błąd standardowy jako σ/√n = 0,5/√100 = 0,05.

7. Pomnóż tę wartość przez wartość z, aby otrzymać błąd statystyczny: 0.05 · 1.959 = 0.098.

8. Dodaj i odejmij błąd statystyczny od wartości średniej, aby uzyskać przedział ufności. W naszym przypadku przedział ufności obejmuje wartości od 2,902 do 3,098.

To wszystko! Całkiem sporo obliczeń, prawda? Na szczęście nasz kalkulator przedziału ufności może wykonać wszystkie te obliczenia za ciebie.

Jednym z niebanalnych zastosowań przedziałów ufności jest analiza szeregów czasowych, gdzie przykładowy zbiór danych reprezentuje ciąg obserwacji w określonym przedziale czasowym.

Bardzo często celem takiego badania jest sprawdzenie, czy zmiana wartości jednego parametru może wpłynąć na wartości innej zmiennej.

Aby być bardziej precyzyjnym, rozważmy następujące pytanie, które często budzi zainteresowanie ekonomistów: Jak zmiana stopy procentowej wpływa na poziom cen?

Jest kilka sposobów podejścia do tego zagadnienia, ale każde z nich wiąże się ze skomplikowaną analizą teoretyczną i empiryczną, która znacznie wykracza poza zakres tego tekstu. Istnieje też wiele technik szacowania i stosowania przedziałów ufności. Mimo wszystko, dokonując pewnych uproszczeń, poprzez ten przykład przedstawimy rolę przedziałów ufności w dość skomplikowanym problemie.

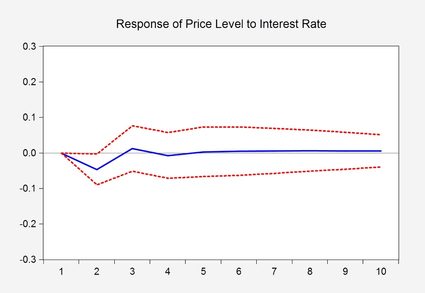
Powyższy wykres jest wizualną reprezentacją wyników estymacji modelu ekonometrycznego, tzw. funkcji odpowiedzi impulsowej, która pokazuje reakcję pewnej zmiennej na zmianę innego parametru. Czerwone przerywane linie poniżej i powyżej niebieskiej krzywej reprezentują 95% przedziały ufności (czasami mówi się o paśmie ufności), które definiują obszar najbardziej prawdopodobnych wartości. Widzimy, że po zmianie stopy procentowej istotna zmiana poziomu cen pojawia się dopiero w drugim miesiącu.

Mamy nadzieję, że dzięki powyższym przykładom i wyjaśnieniom lepiej rozumiesz pojęcie przedziału ufności i nabierasz ochoty na skorzystanie z naszego kalkulatora przedziału ufności.

Jeżeli będziemy wielokrotnie pobierać próbki i wykorzystywać każdą z nich do znalezienia kilku 95% przedziałów ufności dla średniej populacji, to prawdziwa średnia populacji będzie zawarta w około 95% tych przedziałów ufności. Pozostałe 5% przedziałów nie będzie zawierało prawdziwej średniej populacji.

Wartość z dla dwustronnego 95% przedziału ufności wynosi 1,959. Jest to też 97,5 kwantyl standardowego rozkładu normalnego N(0,1).

Wartość z dla dwustronnego 99% przedziału ufności wynosi 2,807. Jest to też 99,5 kwantyl standardowego rozkładu normalnego N(0,1).

Długość przedziału ufności zwiększa się, gdy zwiększa się błąd statystyczny, co ma miejsce, gdy:

• Wzrasta poziom istotności;

• Zmniejsza się wielkość próby; lub

• Zwiększa się wariancja próby.

Długość przedziału ufności maleje, gdy zmniejsza się błąd statystyczny, co ma miejsce, gdy:

• Zmniejsza się poziom istotności;

• Zwiększa się wielkość próby; lub

• Zmniejsza się wariancja próby.

Średnia z próby nie ma wpływu na szerokość przedziału ufności!