Kalkulator przesunięcia fazowego

Witaj w Omni kalkulatorze przesunięcia fazowego, w którym przeanalizujemy funkcje trygonometryczne oraz dostępne sposoby obliczania ich przesunięcia fazowego. W rzeczywistości zajmiemy się czymś więcej: wyjaśnimy również, jak znaleźć amplitudę i okres danej funkcji. W rzeczywistości okazuje się, że ogromna klasa funkcji zachowuje się praktycznie tak samo, a różnice sprowadzają się do opisania właśnie tych wspomnianych wartości: amplitudy, okresu i przesunięcia fazowego. Cóż, przynajmniej w przypadku przesunięcia pionowego wykresu funkcji.

Jak wspomnieliśmy w poprzedniej sekcji, skupimy się tutaj na funkcjach trygonometrycznych: a dokładniej na sinusie i cosinusie. Niemniej jednak ważne jest, aby pamiętać, że wiele pojęć jest bardziej ogólnych, zwłaszcza te dotyczące przesunięcia poziomego wzdłuż osi X lub przesunięcia pionowego.

Po pierwsze, spójrzmy na grafikę pokazującą gdzie amplituda, okres, przesunięcie fazowe i przesunięcie pionowe pojawiają się na wykresie (zauważ, że ten sam obrazek pojawia się na górze kalkulatora przesunięcia fazowego Omni).

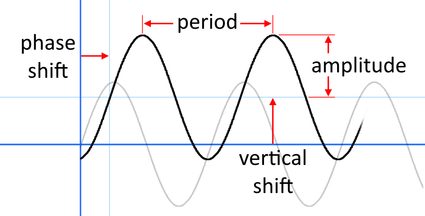
Możemy zapisać takie funkcje za pomocą wzoru (czasami nazywanego równaniem przesunięcia fazowego lub wzorem przesunięcia fazowego):

lub:

gdzie $A$, $B$, $C$, $D$ są dowolnymi liczbami rzeczywistymi, ale $A$ i $B$ przyjmują wartości niezerowe (w przeciwnym razie nie byłaby to funkcja trygonometryczna). Oczywiście te cztery liczby określają amplitudę, okres, przesunięcie fazowe i przesunięcie pionowe. W pewnym stopniu obrazek sugeruje, jak wpływają one na wykres. Przydałoby się jednak poprzeć wizualizacje kilkoma definicjami.

1. Amplituda to odległość (w obie strony) wartości od linii środkowej wykresu. W przypadku prostego sinusa lub cosinusa jej wartość wynosi $1$, ponieważ linia środkowa znajduje się na $0$, a wartości funkcji mieszczą się w zakresie od $-1$ do $1$.

2. Okres to długość na osi poziomej, po której funkcja zaczyna się powtarzać. Innymi słowy, (nieskończony) wykres jest po prostu grupą kopii długości okresu sklejonych ze sobą na końcach. Dla prostego sinusa lub cosinusa okres jest równy $2\pi$ od $\sin(0) = \sin(2\pi) = \sin(4\pi) = ...$ i części pomiędzy są dokładnie takie same (i podobnie dla cosinusa).

3. Przesunięcie fazowe (zwane również przesunięciem poziomym lub przesunięciem wykresu wzdłuż osi X) opisuje, jak daleko w poziomie wykres został przesunięty w stosunku do zwykłego sinusa lub cosinusa. Jako taka, wartość jest równa $0$, jeśli mamy dwie niezmienione funkcje.

4. Przesunięcie pionowe opisuje, jak daleko w pionie wykres został przesunięty w stosunku do zwykłego sinusa lub cosinusa. Innymi słowy, jest to bliźniak przesunięcia fazowego, który dotyczy kierunku prostopadłego. W szczególności wartość jest ponownie równa $0$, jeśli mamy dwie niezmienione funkcje.

W porządku, dowiedzieliśmy się, czym jest przesunięcie fazowe, a także trzy towarzyszące mu wartości. Poniższe sekcje opisują jak obliczyć każdą z nich na podstawie notacji z powyższego wzoru na przesunięcie fazowe. Najpierw pokażemy jak znaleźć amplitudę.

Wprowadzone przez nas pojęcie jest szeroko stosowane w badaniach ruchów oscylacyjnych i harmonicznych. Mówiąc wprost, zjawiska te są najlepszymi kumplami trygonometrii. Możesz odkryć ten związek w naszym kalkulatorze trygonometrycznym lub dowiedzieć się więcej o różnych funkcjach, które pojawiają się podczas analizy wahadła w kalkulatorze funkcji trygonometrycznych 🇺🇸 — lub bardziej szczegółowym kalkulatorze cosinusów 🇺🇸 i kalkulatorze sinusów 🇺🇸!

Wiemy, że funkcje sinus i cosinus przyjmują wartości z zakresu od $-1$ do $1$. Co więcej, ten prosty fakt nie zmienia się, jeśli zastąpimy $\sin(x)$ lub $\cos(x)$ przez $\sin(Bx - C)$ bądź $\cos(Bx - C)$ przez niezerową $B$ i dowolną $C$. W rzeczywistości dzieje się tak dlatego, że funkcja $f(x) = Bx - C$ jest wtedy bijekcją (tj. funkcją wzajemnie jednoznaczną, korespondencją 1:1) na przestrzeń liczb rzeczywistych.

Zobaczmy teraz, co się stanie, jeśli dodamy $D$, tj. jeśli zamiast tego mamy $\sin(Bx - C) + D$ lub $\cos(Bx - C) + D$. Ponieważ pierwsza część daje wynik pomiędzy $-1$ i $1$, a całość będzie pomiędzy $-1 + D$ i $1 + D$ (zobacz jak znaleźć przesunięcie pionowe dla porównania). To oznacza, że linia środkowa wypada na $D$, a amplituda to wciąż $1$, ponieważ wartości wypadają w odległości nawet o $1$ od $D$.

Dlatego jedyną rzeczą, która może wpływać na amplitudę we wzorach na przesunięcie fazowe $A\cdot\sin(Bx - C) + D$ i $A\cdot\cos(Bx - C) + D$ jest niezerowa $A$. I rzeczywiście, ponieważ $\sin(Bx - C)$ i $\cos(Bx - C)$ niezmiennie przyjmują wartości pomiędzy $-1$ i $1$, mnożnik $A$ zmienia ten zakres na $-1\cdot A = -A$ i $1 \cdot A = A$.

Tak, zgadłeś/aś: amplituda równań przesunięcia fazowego $A \cdot\sin(Bx - C) + D$ i $A \cdot\cos(Bx - C) + D$ jest po prostu równa $A$.

Przypomnijmy, że funkcje sinus i cosinus mają okresy równe $2\pi$, tzn. mamy $\sin(x + 2\pi) = \sin(x)$ i $cos(x + 2\pi) = cos(x)$ dla dowolnego $x$. W szczególności daje to:

oraz:

Widzimy więc, że $A$ i $D$ we wzorze na przesunięcie fazowe nie mają wpływu na okres. Rzeczywiście, wszystko sprowadza się do tego co dzieje się wewnątrz funkcji trygonometrycznych.

oraz:

Zgodnie z tymi samymi zasadami, co powyżej, czynnik $C$ nie jest tym, który wykonuje zadanie. Tak więc, po odrzuceniu trzech opcji, musi to być czwarty parametr: $B$.

Ponownie zwracamy się do komentarza, od którego zaczęliśmy, aby zrozumieć, dlaczego i jak $B$ wpływa na okresowość w równaniach przesunięcia fazowego $A \cdot \sin(Bx - C) + D$ i $A \cdot \cos(Bx - C) + D$. Na tej podstawie możemy sformułować poniższe równanie:

Tak więc z każdym $2\pi/B$ dodanym do argumentu $x$, trafiamy z powrotem w to samo miejsce, a funkcja się powtarza (i podobnie dla cosinusa).

Podsumowując, okres równania przesunięcia fazowego jest równy $2\pi/B$.

Nasza codzienna wiedza o falach zazwyczaj przedkłada częstotliwość nad okres, jednak w istocie są one prawie tym samym. Dowiedz się, dlaczego tak się dzieje z Omni kalkulatorem częstotliwości.

Z definicji przesunięcie fazowe opisuje poziome przesunięcie funkcji względem regularnej funkcji $\sin(x)$ lub $\cos(x)$. Jako takie, podstawowe funkcje mają je równe $0$. W rzeczywistości, jeśli porównamy ich wykresy:

...zauważmy, że możemy uzyskać jedną z nich, przesuwając poziomo drugą o określony wektor (w rzeczywistości wzajemne kofunkcje mają wiele podobieństw). Mówiąc dokładniej, możemy na tej podstawie ukształtować poniższe równania:

oraz:

Powyższy przykład sugeruje już, gdzie w $A \cdot\sin(Bx - C) + D$ i $A \cdot\cos(Bx - C) + D$, powinniśmy szukać wartości odpowiedzialnych za przesunięcia fazowe. Jednak w przeciwieństwie do amplitudy i okresu, tym razem będziemy potrzebować dwóch z czterech zmiennych.

Ogólnie rzecz biorąc (czyli nie tylko w równaniach przesunięcia fazowego), otrzymujemy przekształcenie poziome dowolnej funkcji $f(x)$ obliczając $f(x - a)$: przesunięcie wykresu o wektor $a$ w prawo. Innymi słowy, zastępujemy każde wystąpienie $x$ z $x - a$ we wzorze na $f(x)$. Na przykład, zastosowanie tej operacji do $\sin(x)$ daje $\sin(x - a)$, ale dla, powiedzmy, $\cos(3x + 1)$ otrzymamy już:

Innymi słowy, nie możemy zapominać o mnożnikach stojących przed $x$.

W naszym przypadku wzór na przesunięcie fazowe daje:

co jest przesunięciem fazowym $C/B$ (w prawo) funkcji $A \cdot\sin(Bx)$. Oczywiście możemy powtórzyć powyższe działania także dla cosinusa.

Podsumowując, aby obliczyć przesunięcie fazowe, musisz znaleźć $C/B$.

Jest to bardzo proste, zwłaszcza teraz, gdy zobaczyliśmy, czym są przesunięcie fazowe, amplituda i okres oraz jak je obliczyć. Rozwińmy to, czego nauczyliśmy się do tej pory.

Wiemy, że we wzorach na przesunięcie fazowe $A \cdot\sin(Bx - C) + D$ i $A \cdot\cos(Bx - C) + D$, $A$ określa, jak daleko wartości wahają się po obu stronach linii środkowej. Z kolei $B$ określa, jak daleko rozciągamy nierówności wykresu i w rezultacie, jak szybko powtarzają się wartości. Ponadto, wraz z $C$, oba opisują, czy przesunęliśmy funkcję w lewo, czy w prawo i o ile.

Oczywiście przesunięcie poziome nie wpływa na przesunięcie pionowe: w końcu są to dwa prostopadłe kierunki. Z drugiej strony amplituda mówi nam, jak daleko w pionie sięga wykres, ale nie przesuwa go. W skrócie pozostaje nam tylko jedna litera: $D$.

$D$ w równaniach przesunięcia fazowego jest właśnie przesunięciem pionowym. Określa zakres funkcji, tj. jak daleko od zwykłej, nie-$D$ wersji przesuwamy wykres.

Na tym kończymy część teoretyczną. Czas zobaczyć, jak obliczyć przesunięcie fazowe na fajnym przykładzie. Pokażemy też jak znaleźć okres, amplitudę i przesunięcie pionowe. W końcu, dlaczego nie? Więcej matmy = więcej zabawy!

Zobaczmy, jak znaleźć amplitudę, okres, przesunięcie fazowe i przesunięcie pionowe funkcji $f(x) = 0.5 \cdot\sin(2x - 3) + 4$.

W górnej części naszego narzędzia musimy wybrać funkcję, która pojawia się w naszym wzorze. W naszym przypadku wybieramy „sinus” w sekcji „Funkcja trygonometryczna w f” Spowoduje to symboliczną reprezentację takiego równania przesunięcia fazowego: $f(x) = A \cdot\sin(Bx - C) + D$. Patrząc wstecz na to, co mamy, wprowadzamy następujące dane:

Zauważ, że jeszcze przed wprowadzeniem wartości, kalkulator przesunięcia fazowego wyświetla wykres funkcji $\sin(x)$. Dzieje się tak, ponieważ narzędzie rozumie brak wprowadzenia danej wartości. W związku z tym odczytuje brak danych wejściowych jako $A = 1$, $B = 1$, $C = 0$, i $D = 0$, co daje:

W momencie, gdy podamy ostatnią wartość, wykres funkcji pojawi się pod spodem wraz z amplitudą, okresem, przesunięciem fazowym i przesunięciem pionowym. Zauważ również, że w razie potrzeby możesz przejść do trybu zaawansowanego (ang. advanced mode) kalkulatora, aby znaleźć wartość funkcji w dowolnym punkcie $x_0$.

Teraz wyjaśnijmy jak samodzielnie znaleźć przesunięcie fazowe i wszystkie inne wartości. W tym celu wystarczy przypomnieć sobie jak cztery sekcje powyżej tłumaczyliśmy matematykę stojącą za tym zadaniem:

• Amplituda to $A = 0,\!5$;
• Okres wynosi $2\pi / B = 2\pi / 2 = \pi$;
• Przesunięcie fazowe to $C / B = 3 / 2 = 1,\!5$;
• Przesunięcie pionowe wynosi $D = 4$.

Wykres wygląda wówczas następująco:

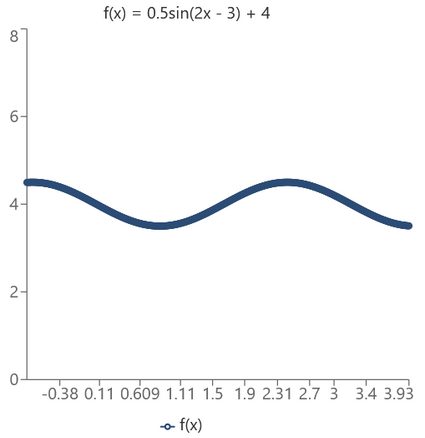
Bułka z masłem, prawda? Pamiętaj, aby pobawić się kalkulatorem przesunięcia fazowego i zobaczyć, jak różne współczynniki wpływają na wykres.

Aby obliczyć przesunięcie fazowe funkcji postaci A ⋅ sin(Bx - C) + D lub A ⋅ cos(Bx - C) + D, musisz:

1. Określić B.
2. Znaleźć C.
3. Podzielić C/B.
4. Pamiętać, że jeśli wynik jest:
   • dodatni, wykres jest przesunięty w prawo.
   • ujemny, wykres jest przesunięty w lewo.
5. Gratulacje, właśnie znalazłeś/aś przesunięcie fazowe.

Aby znaleźć przesunięcie fazowe na wykresie, musisz:

1. Określić czy jest to przesunięta funkcja sinus, czy cosinus.
2. Spojrzeć na wykres po prawej stronie osi pionowej.
3. Znaleźć:
   • maksimum, jeśli współczynnik przed funkcją jest dodatni;
   • minimum, jeśli współczynnik jest ujemny.
4. Obliczyć odległość od osi pionowej do tego punktu.
5. Jeśli funkcja była sinusem, odejmij π/2 lub 3π/2 od tej odległości, odpowiednio dla maksimum lub minimum.
6. Gratulacje, właśnie znalazłeś/aś przesunięcie fazowe z wykresu.

Znajdź amplitudę, okres i przesunięcie fazowe funkcji postaci A ⋅ sin(Bx - C) + D lub A ⋅ cos(Bx - C) + D w następujący sposób:

• Amplituda jest równa A.
• Okres jest równy 2π / B.
• Przesunięcie fazowe jest równe C / B.

Aby wykreślić funkcje trygonometryczne z przesunięciem fazowym, musisz:

1. Określić, jaka to funkcja trygonometryczna.
2. Skupić się na punkcie (0,0) na płaszczyźnie.
3. Jeśli przesunięcie fazowe jest:
   • dodatnie, przesuń w prawo.
   • ujemne, przesuń w lewo.
4. Przesuń wykres na odległość określoną przez przesunięcie fazowe.
5. To miejsce jest punktem początkowym.
6. Narysuj wykres funkcji bez przesunięcia, tak jakby punkt był w miejscu (0,0).
7. Gratulacje, narysowałeś/aś wykres funkcji trygonalnej z przesunięciem fazowym.

Jeśli chodzi o funkcje trygonometryczne, tak. Zwykle rezerwujemy termin „przesunięcie fazowe” dla funkcji trygonometrycznych. Innymi słowy, przesunięcie pionowe może wystąpić dla dowolnego wykresu lub funkcji. Jeśli jednak w rzeczywistości jest to funkcja trygonometryczna, możemy to przesunięcie poziome nazwać przesunięciem fazowym.