Calculateur d'aire totale des solides

Ce calculateur d'aire totale des solides vous aide à trouver l'aire totale des solides tridimensionnels les plus courants. Si vous vous êtes déjà demandé comment trouver l'aire totale d'un solide ou ce que signifie l'aire latérale, alors ce calculateur est fait pour vous. L'aire et l'aire totale ont de nombreuses applications dans différents domaines, comme l'aérodynamique.

Dans cet article, vous trouverez les formules de l'aire d'une sphère, d'un cube, d'un cylindre, d'un cône, d'une pyramide, ainsi que des prismes rectangulaire et triangulaire. Nous vous expliquerons également comment calculer l'aire d'une sphère à titre d'exemple.

L'aire totale d'un solide est la somme des aires de chacune de ses faces. En d'autres termes, c'est l'aire totale d'un objet en 3D. Pour désigner l'aire totale d'un solide, on parle aussi simplement de l'aire d'un solide.

L'aire totale peut être divisée en une somme de l'aire des bases et de l'aire des faces latérales. L'aire des faces latérales est l'aire de tous les côtés de l'objet, à l'exclusion de sa base et de son sommet. Cette division est utilisée pour les formes où il existe une distinction évidente entre la base et les faces latérales ; par exemple, pour un cylindre, un cône, une pyramide ou un prisme triangulaire. Elle est rarement appliquée aux solides dont on ne sait pas exactement quelles faces doivent être considérées comme des bases (comme pour un cube ou un pavé droit), et nous ne l'utilisons pas pour les solides lisses tels qu'une sphère.

Notre calculateur d'aire totale des solides permet de trouver l'aire totale de sept solides différents. La formule dépend du type de solide.

• Aire d'une sphère : A = 4πr²
  où :
  r – le rayon de la sphère

• Aire d'un cube : A = 6a²
  où :
  a – la longueur d'un côté

• Aire d'un cylindre : A = 2πr² + 2πrh
  où :
  r – le rayon
  h – la hauteur du cylindre

• Aire d'un cône : A = πr² + πr√(r² + h²) 
  où :
  r – le rayon
  h – la hauteur du cône

• Aire d'un parallélépipède rectangle (pavé droit) : A = 2(ab + bc + ac)
  où :
  a, b et c – les longueurs des trois côtés du parallélépipède rectangle

• Aire d'un prisme triangulaire : A = 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) + h × (a + b + c)
  où :
  a, b et c – les longueurs des trois côtés de la base du prisme triangulaire
  h – une hauteur (longueur) du prisme

• Aire d'une pyramide : A = l × √(l² + 4 × h²) + l²
  où :
  l – la longueur d'un côté de la base au carré
  h – la hauteur d'une pyramide.

Mais d'où viennent ces formules ? Comment trouver l'aire des formes 3D de base ? Poursuivez votre lecture et vous le saurez !

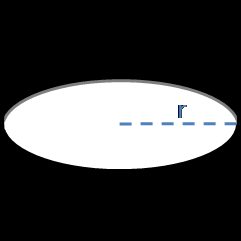
Pour calculer l'aire d'une sphère, il suffit de connaître son rayon (ou son diamètre).

• A = 4 × π × r²
  où : r – le rayon

Comme nous savons que le diamètre d'une sphère est égal à deux fois le rayon, soit d = 2r, nous pouvons écrire l'équation d'une autre manière :

• A = 4 × π × (d / 2)² = π × d²
  où : d – le diamètre de la sphère

Pour déterminer l'aire d'une sphère, il est nécessaire d'utiliser le calcul intégral. Si vous souhaitez en savoir plus, consultez cette démonstration.

Pour déterminer l'aire totale d'un cylindre, vous devez disposer de deux valeurs : le rayon (ou diamètre) d'une base et la hauteur du cylindre. L'équation générale est la suivante : aire des bases plus aire de la face latérale. Dans notre cas, la base est un cercle.

• A = 2πr² + 2πrh

D'où vient cette formule  ? Vous pouvez écrire l'équation de l'aire d'un cylindre comme suit :

• A = A(latérale) + 2 × A(base)

Il est facile de trouver l'aire d'une base ; nous nous souvenons de la formule bien connue pour l'aire d'un cercle : A(base) = π × r². Mais quelle est l'équation de l'aire latérale ? Essayez d'imaginer que nous « déplions » la partie latérale du cylindre. Reconnaissez-vous cette forme ? C'est un rectangle ! L'un des côtés est la hauteur du cylindre, et le second est la circonférence du cercle dépliée.

• A(base) = π × r²
• A(latérale) = h × (2 × π × r)

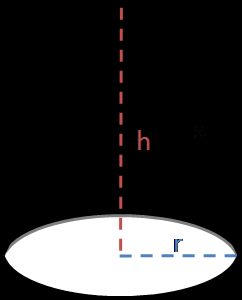
Nous pouvons diviser l'aire totale d'un cône en deux parties :

• A = A(latérale) + A(base)

Nous n'avons qu'une seule base, contrairement à un cylindre.

La base est à nouveau l'aire d'un cercle A(base) = π × r², mais les paramètres de l'aire latérale ne sont peut-être pas aussi évidents :

• A(latérale) = π × r × √(r² + h²)

Décomposons le calcul de l'aire latérale étape par étape :

1. Déroulez la partie latérale à plat. On obtient un secteur circulaire, c'est-à-dire une portion de cercle dont le rayon est s (s est la hauteur oblique du cône).

2. Pour le cercle de rayon s, la circonférence est égale à 2 × π × s. La longueur de l'arc de cercle est égale à 2 × π × r.

3. L'aire du secteur (qui est l'aire latérale de notre cône) est donnée par la formule suivante :

• A(latérale) = (s × (longueur de l'arc de cercle)) / 2 = (s × 2 × π × r) / 2 = π × r × s

  Cette formule peut être obtenue en utilisant les proportions, car le rapport entre les aires des formes est équivalent au rapport entre la longueur de l'arc de cercle et la circonférence :

  (aire du secteur) / (aire du cercle) = (longueur de l'arc de cercle) / (circonférence du cercle)

  Ce qui nous donne :

  (aire du secteur) / (π × s²) = (2 × π × r) / (2 × π × s)

  (aire du secteur) = (π × s²) × (2 × π × r) / (2 × π × s)

• A(latérale) = π × r × s

  Pour trouver le terme manquant de ce rapport, vous pouvez également utiliser notre calculateur de ratio 🇺🇸 !

4. En général, nous n'avons pas la valeur de s mais de h, qui est la hauteur du cône. Mais ce n'est pas un problème du tout ! Nous pouvons facilement transformer la formule en utilisant le théorème de Pythagore :

• r² + h²= s²

  Ainsi, en prenant la racine carrée, on obtient :

  s = √(r² + h²)

  Et donc, la formule de l'aire latérale se présente comme suit :

• A(latérale) = π × r × √(r² + h²)

5. Enfin, additionnez l'aire de la base et l'aire latérale pour trouver la formule finale de l'aire totale d'un cône.

• Si r et s sont donnés : A = A(latérale) + A(base) = π × r × s + π × r².
• Si r et h sont donnés :A = π × r × √(r² + h²) + π × r².

L' aire totale d'un cube 🇺🇸 est la plus simple formule que vous puissiez imaginer : chacune des faces est un carré ! Comme chaque cube a six faces carrées identiques, l'aire est égale à :

• A = 6 × (aire d'un côté)

Comme l'aire d'un carré est le produit de la longueur de ses côtés, la formule finale pour l'aire d'un cube est :

• A = 6 × l²
  où : l – un côté du carré

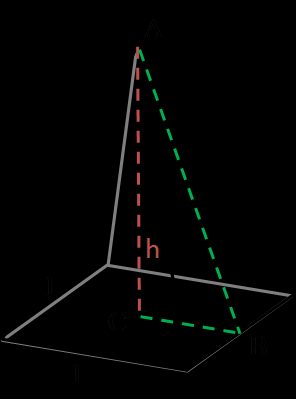
Une pyramide est un solide en 3D avec une base polygonale et des faces latérales triangulaires. Lorsque vous entendez une pyramide, on suppose généralement qu'il s'agit d'une pyramide régulière à base carrée. Mais selon la forme de la base, il peut aussi s'agir d'une pyramide hexagonale ou d'une pyramide rectangulaire. Régulière signifie que sa base est un polygone régulier et que la pyramide est droite, c'est-à-dire que son sommet est situé directement au-dessus du centroïde de sa base. Carrée signifie que sa base est de cette forme. Nous avons utilisé une pyramide régulière à base carrée dans ce calculateur d'aire totale des solides.

La formule pour calculer l'aire totale d'une pyramide est la suivante :

• A = l × √(l² + 4 × h²) + l²
  où :
  l – un côté de la base
  h – une hauteur de la pyramide

Une fois de plus, nous pouvons diviser l'équation en :

A = A(base) + A(latérale) = A(base) + 4 × A(face latérale)

La base ayant la forme d'un carré : A(base) = l². Pour calculer l'aire latérale, commençons par l'aire d'une face triangulaire :

1. Pour trouver la hauteur du triangle, nous aurons à nouveau besoin de la formule de l'hypoténuse :

   c = √(a² + b²)

2. Calculez l'hypoténuse du triangle ABC (qui est en même temps la hauteur de la face triangulaire) :

   c = √(h² + (l/2)²) = √(h² + l²/4)

3. L' aire d'un triangle (dans notre cas, il s'agit d'un triangle isocèle) peut être calculée comme suit :

   A = hauteur × base / 2

   donc,

   A(face latérale) = √(h² + l²/4) × l / 2

4. La formule finale pour l'aire d'une pyramide est :

   A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)

   A = l² + l × √(4 × h² + l²)

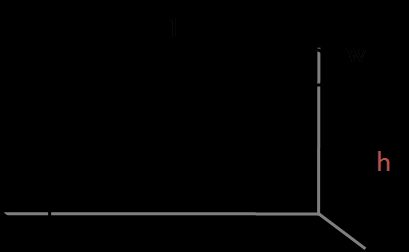
Pour calculer l'aire d'un parallélépipède rectangle, il suffit de calculer les aires des côtés rectangulaires :

• A = 2 × (A1 + A2 + A3)

où :

• A1 = L × l
• A2 = l × h
• A3 = L × h

La formule finale est donc la suivante :

• A = 2 × (L × l + l × h + L × h)

avec :

L – longueur
l – largeur
h – hauteur

Pour comprendre d'où vient la formule de l'aire totale d'un prisme triangulaire, examinons cette démonstration :

1. L'aire latérale est facile à calculer dans ce cas. Comme vous pouvez le voir sur l'image, il s'agit de trois rectangles ayant une longueur de côté en commun :

   A(latérale) = a × h + b × h + c × h = h × (a + b + c)

   On peut aussi réécrire cette équation comme suit :

   A(latérale) = h × P
   où : P – le périmètre de l'une des bases triangulaires

2. Trouvez ensuite l'aire de l'une des bases triangulaires. Vous pouvez le faire de plusieurs façons, en fonction des informations que vous avez. Dans notre calculateur, nous avons implémenté le calcul basé sur la formule de Héron 🇺🇸. Elle est utilisée lorsque vous connaissez les trois côtés d'un triangle (CCC).

   A(base) = 0,25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

3. La formule finale de l'aire d'un prisme triangulaire :

   A = A(latérale) + 2 × A(base)

   a = h × (a + b + c) + 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

Vous pouvez calculer l'aire de n'importe quel solide, par exemple votre corps. Vous remarquerez qu'ici, on parle de « surface » corporelle et non d'aire corporelle. C'est un abus de langage, nous calculons bien l'aire totale du corps. Si vous êtes curieux ou curieuse de savoir quelle est l'aire totale extérieure d'un corps humain, consultez ce calculateur de BSA (surface corporelle).

Si vous voulez trouver l'aire d'une sphère, vous devez suivre ces étapes :

1. Déterminez le rayon de la sphère. Supposons que le rayon est de 10 cm.

2. Entrez cette valeur dans la formule ci-dessous :

   A = 4πr²

3. Calculez le résultat :

   A = 4π × 10² = 1 256 cm²

4. Vous pouvez également utiliser un calculateur d'aire totale des solides en ligne pour trouver le rayon de la sphère si vous connaissez son aire.

Les unités utilisées pour l'aire sont toujours des unités de longueur élevées au carré. Par exemple, vous pouvez l'exprimer en cm², in², ft², m², mais aussi en acres et en hectares.

Si vous souhaitez trouver le volume de l'un de ces solides, utilisez notre calculateur de volume pour le faire.

Pour calculer le côté d'un cube à partir de son aire, procédez comme suit :

1. Notez l'aire de votre cube.
2. Divisez-la par six. Le résultat est l'aire d'une face.
3. Prenez la racine carrée du nombre obtenu à l'étape 2.
4. C'est la longueur de chaque côté de votre cube. Bravo !

Pour déduire le rayon d'une sphère à partir de son aire :

1. Écrivez l'aire de la sphère.
2. Divisez-la par 4π ≈ 12,566.
3. Prenez la racine carrée : √(aire / 4π).
4. Et voilà, c'est le rayon ! Vous pouvez vérifier votre résultat en utilisant un calculateur d'aire totale des solides en ligne.

La réponse est 50,265 5 cm². Pour trouver ce résultat, rappelez-vous que la formule de l'aire d'un cylindre est :

A = 2πr(r + h)

En écrivant r = h = 2, on obtient A = 16π ≈ 50,265 5. N'oubliez pas les unités ! Puisque r et h sont en cm, l'aire est en cm².