Dernière mise à jour le: 29 Nov 2024

Calculateur d'hypoténuse

Q: Comment calculer l'hypoténuse d'un triangle rectangle avec le cosinus ?

Calculez le cosinus de l'angle (mais pas de l'angle droit). Divisez la longueur du côté adjacent à l'angle que vous avez utilisé à l'étape 1 par le résultat obtenu à cette même étape. Vous obtenez ainsi la longueur de l' hypoténuse .

Q: L'hypoténuse est-elle toujours le côté le plus long d'un triangle ?

Oui, dans le cas des triangles rectangles, l'hypoténuse reste toujours le côté le plus long . Pour les triangles isocèles, les deux côtés égaux sont les côtés adjacents, tandis que dans un triangle équilatéral, tous les côtés sont simplement appelés côtés.

Q: Comment calculer les côtés d'un triangle rectangle avec l'hypoténuse ?

Si vous voulez calculer les côtés adjacents d'un triangle rectangle avec l'hypoténuse , vous avez deux options : Si vous connaissez l'un des angles aigus, a = c × cos( θ ) b = c × sin( θ ) où : θ – l'angle aigu adjacent à a Si vous connaissez l'aire, a = √{[ c 2 + √( c 4 − 16 A 2 )] / 2} b = 2 A / a

Q: Comment trouver la hauteur d'une hypoténuse ?

Tracez la hauteur de l'hypoténuse sur le triangle. Les deux nouveaux triangles que vous avez créés sont similaires entre eux et au triangle d'origine. Divisez la longueur du côté le plus court du triangle initial par l'hypoténuse de ce même triangle. Multipliez le résultat par la longueur du côté restant pour obtenir la longueur de l'altitude. Alternativement, étant donné que les angles des petits triangles sont les mêmes que ceux du triangle d'origine, vous pouvez aussi utiliser la trigonométrie .

Q: Comment calculer l'hypoténuse d'un triangle rectangle avec un angle ?

Si vous connaissez un angle et l'un des côtés adjacents d'un triangle rectangle, vous pouvez régler votre problème à l'aide de la trigonométrie : Calculez le sinus ou le cosinus de l'angle donné. Selon le côté que vous connaissez : divisez le côté opposé à l'angle connu par le sinus de l'angle ; ou divisez le côté adjacent à l'angle connu par le cosinus de l'angle. Et voilà ! Vous savez maintenant comment calculer l'hypoténuse d'un triangle rectangle avec un angle et un côté donnés.

Q: Comment trouver l'hypoténuse d'un triangle rectangle isocèle ?

Trouvez la longueur d'un des côtés qui n'est pas l'hypoténuse . Élevez cette longueur au carré. Doublez le résultat de l'étape 2. Prenez la racine carrée du résultat de l'étape 3. Cela vous donne la longueur de l'hypoténuse .

Q: Qu'est-ce que le théorème de congruence d'un triangle rectangle ?

Le théorème de congruence permet de vérifier si deux triangles rectangles sont congruents ou non. Il énonce que si deux triangles rectangles ont une hypoténuse et un angle aigu identiques, alors ils sont congruents.

Q: D'où vient le mot hypoténuse ?

Le mot hypoténuse vient du grec ancien hypoteinousa , qui signifie « soutenante (d'un angle droit) ». Ce mot vient à son tour de hypo- « en dessous » et teinein « tendu ». Encore une chose pour laquelle nous devons remercier la Grèce antique !

Q: Comment calculer l'hypoténuse d'un triangle rectangle sans Pythagore ?

Pour calculer l'hypoténuse d'un triangle rectangle sans Pythagore , vous devez connaître l'un des côtés adjacents et l'un des angles aigus . Pour calculer l'hypoténuse d'un triangle rectangle avec un angle , utilisez le cosinus ou le sinus : c = a / cos( β ) = b / cos ( α ) = a / sin( α ) = b / sin( β ) où : α – l'angle opposé au côté a β – l'angle opposé au côté b

Nouveau

Sommaire

C'est quoi l'hypoténuse d'un triangle rectangle ?Formule de l'hypoténuse : comment calculer l'hypoténuse d'un triangle rectangle ?Exemple de l'échelle : calcul de l'hypoténuse d'un triangle rectangle avec ce calculateur d'hypoténuse FAQ

Avec ce calculateur d'hypoténuse, découvrez facilement le côté le plus long d'un triangle rectangle. Dans cet article, nous répondrons, entre autres, aux questions suivantes :

C'est quoi l'hypoténuse d'un triangle rectangle ?
Comment effectuer le calcul de l'hypoténuse d'un triangle rectangle ? (en règle générale)
- Comment calculer l'hypoténuse d'un triangle rectangle avec un angle ?
- Comment calculer l'hypoténuse d'un triangle rectangle avec le cosinus ?
- Comment calculer l'hypoténuse d'un triangle rectangle sans Pythagore ?
Comment utiliser ce calculateur d'hypoténuse ?
Comment calculer les côtés d'un triangle rectangle avec l'hypoténuse ?

Les réponses sont ci-dessous accompagnées d'un exemple simple pour vous aider à comprendre. N'hésitez pas à essayer ce calculateur d'hypoténuse dès maintenant !

C'est quoi l'hypoténuse d'un triangle rectangle ?

Triangle rectangle avec angle droit et hypoténuse indiqués.

L'hypoténuse est le plus long côté d'un triangle rectangle. C'est le côté opposé à l'angle droit (90°). La longueur de l'hypoténuse peut être déterminée, par exemple, à partir du théorème de Pythagore. Pour en savoir plus, consultez notre calculatrice du théorème de Pythagore.

Formule de l'hypoténuse : comment calculer l'hypoténuse d'un triangle rectangle ?

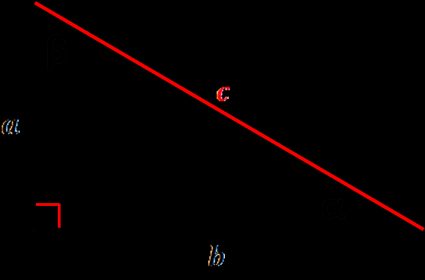
Triangle rectangle avec ses côtes a, b, c and ses angles α and β indiqués.

Ce calculateur d'hypoténuse propose différentes formules pour s'adapter à divers scénarios.

1. Comment calculer l'hypoténuse d'un triangle rectangle avec les côtés adjacents ?

Utilisez le théorème de Pythagore pour calculer l'hypoténuse à partir des deux autres côtés du triangle rectangle. Prenez la racine carrée de la somme des carrés :

c = √(a² + b²)

Triangle rectangle avec formules de la loi des sinus. a sur sin(α) est égal à b sur sin(β). Tous deux égaux à c, car sin(90°) = 1.

2. Comment calculer l'hypoténuse d'un triangle rectangle avec un angle et le cosinus ?

Pour effectuer le calcul de l'hypoténuse d'un triangle rectangle avec un angle, vous devez diviser la longueur du côté adjacent à l'angle donné par le cosinus de l'angle :

c = b/cos(α) = a/cos(β)

Vous pouvez aussi recourir au sinus, si vous préférez :

c = a/sin(α) = b/sin(β)

Cette formule est expliquée dans notre calculateur de la loi des sinus 🇺🇸.

3. Comment calculer l'hypoténuse d'un triangle rectangle avec l'aire et un côté adjacent ?

Le calcul de l'hypoténuse d'un triangle rectangle avec l'aire est plus facile que vous ne pensiez. Comme l'aire d'un triangle rectangle est égale à (a × b) / 2, alors :

c = √(a² + b²) = √(a² + (aire × 2 / a)²) = √((aire × 2 / b)² + b²)

Pour en savoir plus sur les calculs impliquant des triangles rectangles, consultez notre calculateur d'aire d'un triangle rectangle et le calculateur d'angle et de côté d'un triangle rectangle.

Si vous vous demandez comment calculer l'hypoténuse d'un triangle rectangle sans Pythagore ?, c'est tout à fait possible ! Vous devrez vous concentrer la deuxième option, celle avec la trigonométrie.

Exemple de l'échelle : calcul de l'hypoténuse d'un triangle rectangle avec ce calculateur d'hypoténuse

Voyons combien mesure l'échelle dont nous avons besoin pour secourir un chaton d'un toit haut de 3 m. Notre calculateur vous aidera à trouver la longueur nécessaire de l'échelle du sol jusqu'au bord du toit, tout en prenant en compte la portion de l'échelle qui doit dépasser le bord !

Il est très important de comprendre le concept de l'hypoténuse à ce stade. Si vous vous demandez toujours « C'est quoi l'hypoténuse ? », revoyez la définition au début de l'article.

Choisissez l'option nécessaire pour vos calculs. Vous savez que notre toit a une hauteur de 3 m (~ 10 ft) et que l'angle le plus sûr pour une échelle est de ~75,5°. Dans la liste déroulante du champ correspondant, sélectionnez l'option : angle ∡ et un côté.
Changez les unités en mètres.

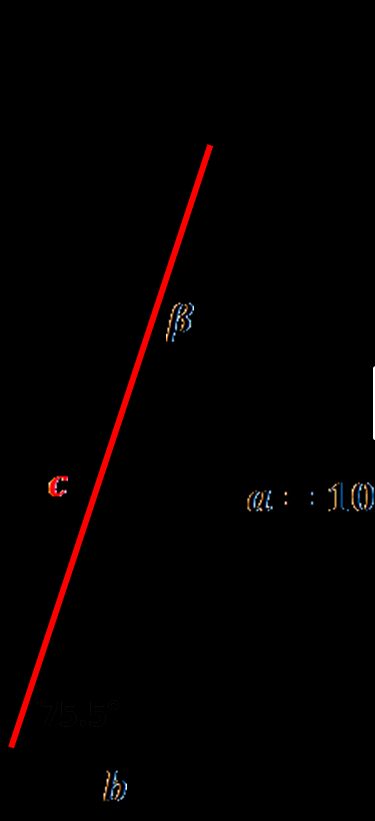
Image simplifiée d'une échelle. Triangle droit avec a = 3 m et angle α égal à 75,5°.

Saisissez les valeurs données. Notre côté adjacent a mesure 3 m de long, et l'angle α entre l'échelle et le sol est égal à 75,5°.
La longueur de l'échelle, soit l'hypoténuse du triangle rectangle, apparaît ! Elle est égale à 3,10 m.

L'angle β est de 14,5° et le côté adjacent b mesure 0,78 m. Le deuxième côté adjacent est également un paramètre crucial, car il indique à quelle distance du mur (ou plutôt du bord du toit) vous devez placer l'échelle. Un principe à retenir est la règle du 4:1, qui indique que pour chaque 1,2 m de hauteur verticale, le pied de l'échelle doit se déplacer de 0,3 m par rapport au mur.

Ce calculateur peut également calculer les côtés d'un triangle rectangle avec l'hypoténuse. Il vous suffira de choisir la deuxième ou la troisième option dans le premier champ de sélection, puis saisir un angle et l'hypoténuse ou l'aire et l'hypoténuse !

FAQ

Comment calculer l'hypoténuse d'un triangle rectangle avec le cosinus ?

Calculez le cosinus de l'angle (mais pas de l'angle droit).
Divisez la longueur du côté adjacent à l'angle que vous avez utilisé à l'étape 1 par le résultat obtenu à cette même étape.
Vous obtenez ainsi la longueur de l'hypoténuse.

L'hypoténuse est-elle toujours le côté le plus long d'un triangle ?

Oui, dans le cas des triangles rectangles, l'hypoténuse reste toujours le côté le plus long. Pour les triangles isocèles, les deux côtés égaux sont les côtés adjacents, tandis que dans un triangle équilatéral, tous les côtés sont simplement appelés côtés.

Comment calculer les côtés d'un triangle rectangle avec l'hypoténuse ?

Si vous voulez calculer les côtés adjacents d'un triangle rectangle avec l'hypoténuse, vous avez deux options :

Si vous connaissez l'un des angles aigus,

a = c × cos(θ)
b = c × sin(θ)

où :
θ – l'angle aigu adjacent à a
Si vous connaissez l'aire,

a = √{[c² + √(c⁴ − 16A²)] / 2}
b = 2A / a

Comment trouver la hauteur d'une hypoténuse ?

Tracez la hauteur de l'hypoténuse sur le triangle. Les deux nouveaux triangles que vous avez créés sont similaires entre eux et au triangle d'origine.
Divisez la longueur du côté le plus court du triangle initial par l'hypoténuse de ce même triangle.
Multipliez le résultat par la longueur du côté restant pour obtenir la longueur de l'altitude.
Alternativement, étant donné que les angles des petits triangles sont les mêmes que ceux du triangle d'origine, vous pouvez aussi utiliser la trigonométrie.

Comment calculer l'hypoténuse d'un triangle rectangle avec un angle ?

Si vous connaissez un angle et l'un des côtés adjacents d'un triangle rectangle, vous pouvez régler votre problème à l'aide de la trigonométrie :

Calculez le sinus ou le cosinus de l'angle donné.
Selon le côté que vous connaissez :
- divisez le côté opposé à l'angle connu par le sinus de l'angle ; ou
- divisez le côté adjacent à l'angle connu par le cosinus de l'angle.
Et voilà ! Vous savez maintenant comment calculer l'hypoténuse d'un triangle rectangle avec un angle et un côté donnés.

Comment construire une droite perpendiculaire à l'hypoténuse ?

Munissez-vous d'un compas, d'une règle et d'un stylo ou d'un crayon.
Prenez la longueur de l'hypoténuse comme écartement de votre compas (ou de n'importe quelle longueur, pourvu qu'elle reste constante).
Dessinez un premier cercle tel que son centre est l'une des extrémités de l'hypoténuse.
Tracez un autre cercle dont le centre se trouve à l'autre extrémité de l'hypoténuse.
Tracez une droite reliant les deux points où les cercles se rencontrent. Cette droite est perpendiculaire à l'hypoténuse.

Comment trouver l'hypoténuse d'un triangle rectangle isocèle ?

Trouvez la longueur d'un des côtés qui n'est pas l'hypoténuse.
Élevez cette longueur au carré.
Doublez le résultat de l'étape 2.
Prenez la racine carrée du résultat de l'étape 3. Cela vous donne la longueur de l'hypoténuse.

Qu'est-ce que le théorème de congruence d'un triangle rectangle ?

Le théorème de congruence permet de vérifier si deux triangles rectangles sont congruents ou non. Il énonce que si deux triangles rectangles ont une hypoténuse et un angle aigu identiques, alors ils sont congruents.

D'où vient le mot hypoténuse ?

Le mot hypoténuse vient du grec ancien hypoteinousa, qui signifie « soutenante (d'un angle droit) ». Ce mot vient à son tour de hypo- « en dessous » et teinein « tendu ». Encore une chose pour laquelle nous devons remercier la Grèce antique !

Comment calculer l'hypoténuse d'un triangle rectangle sans Pythagore ?

Pour calculer l'hypoténuse d'un triangle rectangle sans Pythagore, vous devez connaître l'un des côtés adjacents et l'un des angles aigus.

Pour calculer l'hypoténuse d'un triangle rectangle avec un angle, utilisez le cosinus ou le sinus :

c = a / cos(β) = b / cos (α) = a / sin(α) = b / sin(β)

où :
α – l'angle opposé au côté a
β – l'angle opposé au côté b