Dernière mise à jour le: 27 Jul 2024

Calculateur d'aire d'un triangle rectangle

Q: Comment calculer l'aire d'un triangle avec une hypoténuse de 5 cm et un angle de 45° ?

Vous devez appliquer la formule aire = c² × sin(α) × cos(α) / 2 pour c = 5 et α = 45° . Le théorème mathématique utilisé pour obtenir cette formule s'appelle la loi des sinus . Dans ce cas, l'aire est égale à 6,25 cm² .

Q: Comment appelle-t-on les côtés d'un triangle rectangle ?

Les deux côtés perpendiculaires l'un à l'autre s'appellent côtés adjacents , alors que le côté opposé à l'angle droit, qui est aussi le côté le plus long, est l' hypoténuse .

Sommaire

Formules de l'aire d'un triangle rectangle Aire d'un triangle rectangle isocèle Comment utiliser le calculateur d'aire d'un triangle rectangle ?FAQ

Si vous voulez savoir comment trouver l'aire d'un triangle rectangle, vous êtes au bon endroit ! Ce calculateur d'aire d'un triangle rectangle est l'outil parfait pour vous.

Que vous connaissiez les côtés adjacents, l'hypoténuse et un côté adjacent, ou un côté et un angle autre que l'angle droit, ce calculateur a la réponse.

Poursuivez votre lecture pour en savoir plus sur les formules de l'aire d'un triangle rectangle, ou essayez tout simplement notre calculateur !

Formules de l'aire d'un triangle rectangle

🙋 Si votre triangle n'est pas un triangle rectangle, consultez ce calculateur d'aire d'un triangle.

La formule standard vient de la formule de l'aire de tous les triangles :

$A = \dfrac{a \times h}{2}$

Comme les côtés adjacents du triangle rectangle sont perpendiculaires l'un à l'autre, on peut utiliser cette formule en supposant que l'un de ces côtés soit la base, et l'autre la hauteur.

\text{A}=\frac{a\times b}{2}

Mais parfois ce n'est pas si évident. Que faut-il faire si l'on ne connaît pas les deux côtés adjacents ?

Si l'hypoténuse et un côté adjacent sont donnés, prenez le théorème de Pythagore.

\qquad a^2+b^2=c^2

Ensuite, réarrangez la formule et calculez la racine carrée 🇺🇸 de l'équation pour calculer le côté manquant, par exemple, $b$ :

$b = \sqrt{c^2 - a^2}$

Enfin, reprenez la formule standard et entrez vos données.

\qquad\text{A}=a\times\frac{\sqrt{c^2-a^2}}{2}

Analogiquement, si vous connaissez $b$ , calculez d'abord la longueur de $a$ :

$a = \sqrt{c^2 - b^2}$

Ensuite, trouvez l'aire :

\qquad \text{A} = b\times\frac{\sqrt{c^2-b^2}}{2}

Si vous connaissez l'hypoténuse et un angle autre que l'angle droit, vous pouvez utiliser la loi des sinus 🇺🇸 pour obtenir l'aire.

\qquad a=c\times\sin(\alpha)

Vous pouvez réécrire cette formule comme suit :

\qquad \begin{split} b&=c\times\sin(\beta)\\&=c\times\sin(90\degree-\alpha)\\ &=c\times\cos(\alpha) \end{split}

Donc :

\qquad \text{A}=c^2\times\sin(\alpha)\times\frac{\cos(\alpha)}{2}

Si vous connaissez un côté adjacent et un angle autre que l'angle droit, vous pouvez trouver l'aire à l'aide de la trigonométrie. Voyons les relations trigonométriques que nous allons utiliser :

\qquad\frac{a}{b}=\tan(\alpha)

\qquad\frac{b}{a}=\tan(\beta)

Donc, nous pouvons écrire deux formules. En fonction de $b$ :

\qquad \begin{split} \text{A}&=b\times\tan(\alpha)\times\frac{b}{2}\\ \\[1.5em] &=b^2\times\frac{\tan(\alpha)}{2} \end{split}

En fonction de $a$ :

\qquad \begin{split} \text{A}&=a\times a\times \frac{\tan(\beta)}{2}\\[1em] &=a^2\times\frac{\tan(\beta)}{2} \end{split}

🙋 Vous voulez en savoir plus sur les triangles rectangles ? Consultez notre calculateur de triangle rectangle !

Aire d'un triangle rectangle isocèle

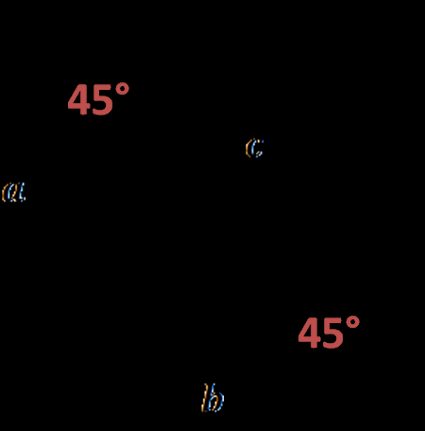
Un triangle rectangle isocèle est un triangle rectangle particulier. Il est parfois appelé triangle 45 45 90, car ses angles font 45°, 45° et 90°. (Si les triangles isocèles vous intéressent, consultez notre calculateur de triangle rectangle isocèle.) Dans un tel triangle, les côtés adjacents sont égaux, et l'hypoténuse est le côté le plus long.

a=b

Si l'on suppose que l'un des côtés adjacents est la base et l'autre la hauteur, et que l'angle entre les deux est l'angle droit, l'aire sera la suivante :

\text{A}=\frac{a^2}{2}

Comment utiliser le calculateur d'aire d'un triangle rectangle ?

Voyons les calculs étape par étape :

Choisissez une option, en fonction des paramètres que vous connaissez. Supposons qu'un côté adjacent et un angle soient donnés. Nous sélectionnerons donc l'option « un angle et un côté ».
Saisissez les valeurs. Disons que $\alpha = 40\degree$ et $b = 17\ \text{cm}$ .
Regardez notre calculateur aire d'un triangle rectangle effectuer tous les calculs pour vous ! L'aire du triangle choisi est égale à $121,\!25\ \text{cm}^2$ .

FAQ

Comment calculer l'aire d'un triangle rectangle à partir de deux côtés ?

La méthode dépend des côtés connus.

Si vous connaissez les deux côtés adjacents, utilisez la formule suivante :

aire = a × b / 2

où :
- a et b – les côtés adjacents

‎

Si vous connaissez un côté adjacent, par exemple, a, et l'hypoténuse, c, voici la formule à utilise :

aire = a × √(c² - a²) / 2

Comment calculer l'aire d'un triangle avec une hypoténuse de 5 cm et un angle de 45° ?

Vous devez appliquer la formule aire = c² × sin(α) × cos(α) / 2 pour c = 5 et α = 45°. Le théorème mathématique utilisé pour obtenir cette formule s'appelle la loi des sinus. Dans ce cas, l'aire est égale à 6,25 cm².

Comment savoir si un triangle est rectangle ?

Si vous connaissez les trois côtés d'un triangle et que vous voulez vérifier si ce triangle est rectangle, utilisez le théorème de Pythagore pour vérifier si la somme des deux cotés adjacents élevés au carré est bien égale au carré de l'hypoténuse : a² + b² = c².

Comment appelle-t-on les côtés d'un triangle rectangle ?

Les deux côtés perpendiculaires l'un à l'autre s'appellent côtés adjacents, alors que le côté opposé à l'angle droit, qui est aussi le côté le plus long, est l'hypoténuse.