Calculateur de triangle rectangle

Le calculateur du triangle rectangle vous assistera dans le calcul des longueurs des côtés d'un triangle rectangle. Il vous montrera également comment déterminer l'aire d'un triangle rectangle et il vous fournira de nombreuses informations sur les applications concrètes du triangle rectangle.

Tout d'abord, définissons un triangle rectangle. L'explication est très simple et peut même sembler évidente pour ceux qui la connaissent déjà : un triangle rectangle est un triangle dont un et seulement un des angles fait exactement 90°. Les deux autres angles seront évidemment inférieurs à un angle droit parce que la somme de tous les angles d'un triangle est toujours égale à 180°.

Dans un triangle rectangle, les côtés sont définis d'une manière particulière. Le côté opposé à l'angle droit est toujours le plus long du triangle et il porte le nom « d'hypoténuse ». Les deux autres côtés sont appelés les « côtés adjacents ». La relation entre l'hypoténuse et chaque côté adjacent est assez simple, comme on le verra quand il sera question du théorème de Pythagore.

Si tout ce que vous voulez calculer est l'hypoténuse d'un triangle rectangle, cet article et notre calculateur du triangle rectangle répondront à vos attentes. Cependant, Omni Calculator a aussi développé un outil dédié que nous vous recommandons également d'utiliser : le calculateur d'hypoténuse. L'hypoténuse est le côté opposé à l'angle droit et peut être déterminée en employant le théorème de Pythagore. Dans un triangle rectangle avec les côtés adjacents a et b et avec l'hypoténuse c, le théorème de Pythagore stipule que : a² + b² = c².

Pour résoudre c, prenez la racine carrée des deux côtés pour obtenir c = √(b²+a²). Nous pouvons considérer cette variation du théorème de Pythagore comme une « formule de l'hypoténuse ». Notre calculateur du théorème de Pythagore est aussi un excellent outil pour calculer l'hypoténuse.

Résolvons maintenant un exemple de problème comportant le calcul de l'hypoténuse d'un triangle rectangle sans utiliser les calculateurs Omni :

1. Établissez les valeurs de a et b.
2. Élevez a et b au carré.
3. Additionnez les deux valeurs obtenues : a² + b².
4. Prenez la racine carrée de la somme.
5. La racine carrée donnera deux résultats : un positif et un négatif. Comme il s'agit d'une longueur, ne tenez pas compte du résultat négatif.
6. La valeur obtenue est la valeur de l'hypoténuse c.

Voyons maintenant ce processus à l'aide des calculateurs Omni, par exemple, le calculateur du triangle rectangle disponible sur ce site :

1. Insérez les valeurs de a et b dans le calculateur.
2. Vous obtiendrez immédiatement la valeur de c.
3. De plus, vous découvrirez aussi la valeur de l'aire d'un tel triangle.

Nous avons déjà vu que calculer l'aire d'un triangle à angle droit est très facile à l'aide du calculateur du triangle rectangle. Chez Omni Calculator, nous mettons également à votre disposition un calculateur conçu dans ce but : le calculateur de l'aire d'un triangle rectangle 🇺🇸. Voyons maintenant en plus de détail comment calculer l'aire d'un triangle rectangle.

La méthode pour trouver l'aire d'un triangle rectangle est assez simple. Tout ce dont vous avez besoin, ce sont les mesures de la base et de la hauteur. Dans un triangle rectangle, la base et la hauteur sont les deux côtés qui forment l'angle droit. Comme la multiplication de ces deux valeurs donnerait l'aire du rectangle correspondant, et que le triangle représente la moitié de ceci, la formule est la suivante :

aire = ½ × base × hauteur

Si vous ne connaissez pas la base ou la hauteur, vous pouvez la trouver en utilisant le théorème de Pythagore. Vérifiez vos résultats avec le calculateur du triangle rectangle. Vous pouvez ainsi calculer l'aire d'un triangle dont les côtés sont plus longs ou ont une valeur décimale.

Nous allons maintenant voir d'autres éléments liés au triangle rectangle que les calculateurs Omni peuvent calculer.

Les côtés d'un triangle ont une pente. La formule de la pente est la suivante :

pente = (y₂ - y₁)/(x₂ - x₁)

Donc pour les coordonnées (1,-6) et (4,8), la pente du segment est égale à (8 + 6)/(4 - 1) = 14/3. Un moyen facile de déterminer si un triangle est rectangle, quand les coordonnées sont connues, est de multiplier les pentes : si le résultat est égal à -1, il s'agit d'un triangle à angle droit.

Il existe une méthode facile pour convertir les radians en degrés et les degrés en radians à l'aide de la conversion d'angles :

• si un angle est exprimé en radians — il faut multiplier par 180/π ; et
• si un angle est exprimé en degrés — multipliez par π/180.

Parfois, on ne connait pas deux ou même trois côtés, et cela peut poser problème. Dans ce cas-là, le calculateur du triangle rectangle, le calculateur de l'hypoténuse et la méthode pour trouver l'aire d'un triangle rectangle ne vous seront d'aucune aide. Vous devrez employer des fonctions trigonométriques pour déterminer les mesures manquantes.

Le triangle rectangle n'est qu'un des nombreux triangles spéciaux qui existent. Ces triangles ont une ou plusieurs caractéristiques particulières qui les rendent uniques. Par exemple, comme nous l'avons vu, le triangle rectangle a un angle droit, et donc une hypoténuse, ce qui en fait un type de triangle unique. À part le triangle rectangle, il existe d'autres triangles spéciaux aux propriétés intéressantes.

L'un des triangles spéciaux les plus connus est le triangle équilatéral, qui a trois côtés égaux et tous ses angles font 60°. Il est donc beaucoup plus simple de calculer les différents paramètres d'un tel triangle en utilisant un calculateur.

Un autre triangle particulier est le triangle isocèle, qui a deux côtés de la même longueur, et par conséquence, deux angles de la même taille. Contrairement au triangle équilatéral, les triangles isocèles ont des formes différentes.

Il existe de nombreux autres triangles spéciaux. Cependant, nous allons maintenant nous intéresser à quelques triangles rectangles très spéciaux qui, en plus d'être des triangles rectangles, possèdent d'autres propriétés uniques qui les rendent intéressants.

Le triangle dit isocèle est probablement le plus spécial de tous les types de triangles rectangles. C'est un triangle rectangle qui est aussi un triangle isocèle. Ses deux côtés adjacents ont la même longueur (isocèle), mais aussi, ses autres angles sont exactement deux fois plus petits que l'angle droit.

Ce triangle rectangle est le type de triangle que vous pouvez obtenir après avoir divisé un carré par sa diagonale. C'est pourquoi les deux côtés adjacents (les côtés du carré) ont la même longueur. Pour ceux qui souhaitent approfondir leurs connaissances sur le plus spécial des triangles rectangles, nous recommandons de consulter le calculateur de triangle rectangle isocèle qui a été conçu à cet effet.

Un autre triangle fascinant du groupe des triangles rectangles spéciaux est le demi triangle équilatéral ou triangle dit triangle 30 60 90. Son nom vient du fait qu'il a un angle droit (90°), un angle de 30° et un autre de 60°. Ces angles sont spéciaux en raison des valeurs de leurs fonctions trigonométriques (cosinus, sinus, tangente, etc.). On peut remarquer cela à l'aide du calculateur de demi triangle équilatéral (30-60-90), mais pour ceux qui n'ont pas assez de temps pour une autre lecture, nous allons résumer les particularités de ces fonctions ci-dessous. Si le côté le plus court a une longueur a, les autres mesures du triangle sont les suivantes :

1. La longueur du deuxième côté est égale à a√3.
2. L'hypoténuse est égale à 2a.
3. L'aire est égale à (a²√3)/2.
4. Le périmètre est égal à a(3 + √3).

À première vue, un triangle rectangle et un parallélogramme n'ont rien en commun. Comment un calculateur de triangles peut-il aider à comprendre ce qu'est un parallélogramme ? En réalité, tout parallélogramme peut être décomposé en deux ou plusieurs triangles rectangles. Voici un exemple qui permet de visualiser cela plus facilement.

Imaginez un rectangle, n'importe lequel. Tracez maintenant une des diagonales de ce rectangle. Si l'on sépare le rectangle par sa diagonale, on obtient deux triangles rectangles. En observant les triangles, il n'y a pas besoin d'utiliser le calculateur du triangle rectangle pour voir que les deux sont égaux, donc que leurs aires sont les mêmes. Cela signifie que l'aire du rectangle est le double de celle de chaque triangle.

Si nous pensons aux équations menant à cette conclusion, c'est logique puisque l'aire d'un rectangle ayant pour côtés a et b est égale à aire = a × b, tandis que dans le cas du triangle rectangle c'est aire = base × hauteur / 2, ce qui, dans ce cas, sera aire = a × b /2. C'est précisément ce que
l'on a déjà vu après avoir coupé le rectangle par la diagonale.

C'est un exemple simple avec un rectangle et le procédé est le même pour un carré. Pour les autres parallélogrammes, cela devient un peu plus compliqué (on peut arriver jusqu'à quatre triangles rectangle de tailles différentes). Néanmoins, avec un peu d'astuce, vous pouvez réutiliser la même idée et calculer l'aire d'un parallélogramme en utilisant des triangles rectangles. Pour encore plus d'efficacité, vous pouvez bien sûr utiliser notre calculateur.

La géométrie et les polygones, en particulier les triangles, vont toujours de pair. Les propriétés de certains triangles, comme les triangles rectangles, sont généralement intéressantes et surprenantes, même pour les non-mathématiciens. Nous allons maintenant examiner un ensemble intéressant de nombres étroitement associés aux triangles rectangles que les mathématiciens adorent, et peut-être que vous les adorerez aussi.

Ces ensembles de nombres s'appellent les triplets de Pythagore. Il s'agit d'ensembles de trois nombres entiers (appelons-les a, b, et c) qui satisfont le théorème de Pythagore : a² + b² = c². Autrement dit, des cotés de longueurs a, b, et c pourraient former un triangle rectangle. La quantité de nombres qui satisfont cette relation est limité, mais les mathématiciens s'amusent à rechercher de nouveaux exemples.

En outre, elle possède quelques autres propriétés intéressantes qui sont exploitées en cryptographie. Étant donné les utilisations possibles pour de tels ensembles de nombres, les mathématiciens ont exploré encore au-delà ; ils ont utilisé quatre ou plus d'ensembles de nombres qui satisfont une relation similaire, c'est-à-dire une relation dans laquelle la somme des carrés de tous les nombres (sauf un) donne le carré du nombre qui reste.

Également très lié à ces triplets de Pythagore est le célèbre dernier théorème de Fermat, dans lequel le mathématicien presque légendaire Pierre Fermat a déclaré qu'un ensemble de trois nombres entiers qui satisferait la relation : aⁿ + bⁿ = cⁿ pour n supérieur à 2 n'existe pas. Cette conjecture n'a été prouvée qu'en 1995, plus de 300 ans après sa formulation, et elle est considérée comme l'un des problèmes mathématiques les plus importants du siècle.

Nous avons beaucoup parlé des triangles, en particulier des triangles rectangles, et de leurs applications en mathématiques et en géométrie. Ce dont nous n'avons pas encore parlé, c'est l'utilité des triangles rectangles pour des calculs dans la vie réelle. On pourrait croire que les applications de tels triangles en dehors de la géométrie sont limitées, mais jetons un coup d'œil aux ombres.

Eh oui, on a bien dit des ombres ! Elles sont projetées par des objets lorsqu'ils sont éclairés. Si l'on observe la position de la forme créée par l'ombre, de l'objet et du sol, on se rend compte qu'il s'agit en fait d'un triangle rectangle ! Du moins, c'est le cas quand l'objet est parfaitement vertical et le sol est horizontal. Cela est vrai la plupart du temps, ou presque. Donc le calculateur du triangle rectangle peut être utilisé pour trouver différentes informations sur des objets éclairés par le soleil. Voici comment faire ça :

Imaginez-vous devant un bâtiment dont vous aimeriez connaître la hauteur. Seulement, il est trop haut pour être mesuré directement avec un mètre ruban. Vous pouvez alors résoudre ce problème en mesurant l'ombre projetée par le bâtiment sur le sol. Ensuite, à l'aide d'un instrument de mesure d'angle simple et d'une feuille de papier, vous pouvez déterminer l'angle entre l'ombre et le sol. Comme l'angle entre le bâtiment et le sol est toujours de 90°, vous pouvez facilement calculer la hauteur de l'immeuble.

Cette technique permet de mesurer la hauteur de nombreux objets si le temps est beau et ensoleillé ou à l'aide d'autres sources de lumière pour éclairer l'objet. En fait, la technique était bien connue auparavant. L'utilisation la plus intéressante et la plus époustouflante des triangles rectangles est probablement celle d'Ératosthène, qui a réussi à utiliser des triangles rectangles et des ombres pour mesurer le rayon de la Terre, et nous allons maintenant vous expliquer comment il s'y est pris.

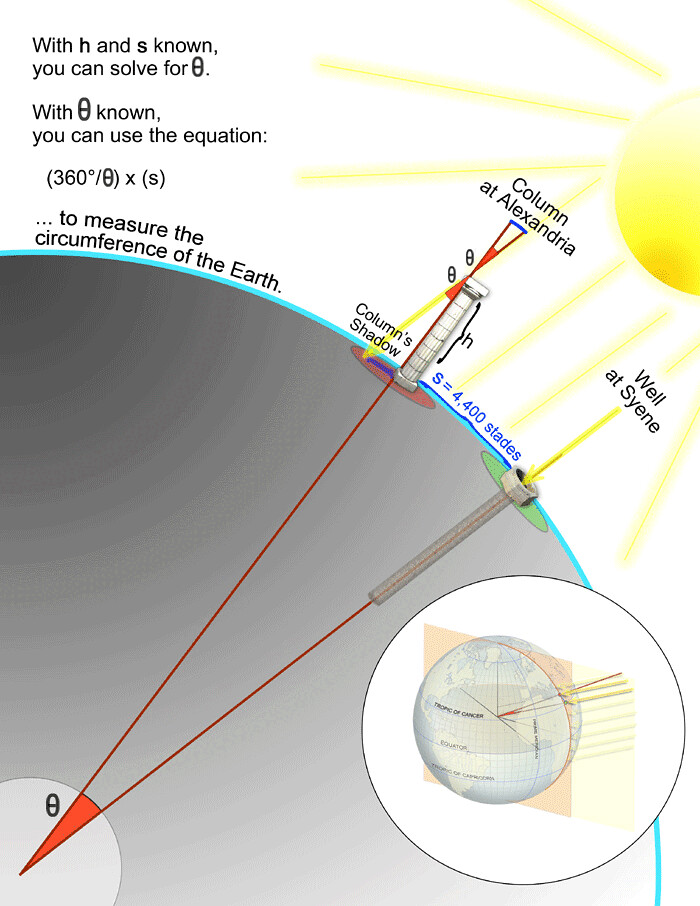
Ératosthène a remarqué que pendant le solstice d'été, il y avait un endroit sur la Terre où, à midi, il n'y avait pas d'ombre dans les puits, c'est-à-dire que le soleil était directement au-dessus. Tenant compte de cela, il a construit une colonne d'une hauteur connue à une distance connue d'un de ces puits et il a mesuré la taille de l'ombre créée par le poteau à midi le jour du solstice. Ensuite, à l'aide de triangles rectangles et de la trigonométrie, il a pu déterminer l'angle partant du centre de la Terre entre le puits et le poteau, ainsi que le rayon de la Terre, étant donné la distance entre ces deux points.

C'était un calcul assez étonnant que vous pouvez réaliser beaucoup plus facilement, en utilisant les calculateurs Omni que nous avons créées pour vous.