Calculadora de la forma pendiente-intersección

Esta calculadora de la forma pendiente-intersección te mostrará cómo hallar la ecuación de una recta a partir de las coordenadas de dos puntos en la recta. Con su ayuda, podrás encontrar la pendiente y ordenada al origen empleando la forma pendiente-intersección de la recta. Continúa leyendo para aprender qué es la forma pendiente-intersección de una ecuación lineal, cómo hallar la ecuación de una recta y como influye la forma pendiente-intersección en la vida real.

Cualquier línea sobre un plano puede describirse matemáticamente como una relación entre las posiciones en el eje vertical (eje y) y horizontal (eje x) de cada uno de los puntos que contribuyen a la recta. Esta relación puede escribirse como y = [algo con x]. La forma concreta de [algo con x] determinará qué tipo de recta tenemos. Por ejemplo, y = x² + x es una parábola, también llamada función cuadrática. En cambio, y = mx + b (con m y b representando números reales cualesquiera) es la ecuación de una recta.

En esta calculadora de la forma pendiente-intersección, nos centraremos en la ecuación de una recta. Puedes consultar nuestra calculadora de razón de cambio promedio para hallar la relación que existe entre las variables de funciones no lineales.

Las ecuaciones lineales, o ecuaciones de la recta, se reconocen rápidamente porque no contienen términos con exponentes. (Por ejemplo, encontrarás una x o una y, pero nunca una x².) Cada ecuación lineal describe una línea recta, que puede expresarse mediante su ecuación de forma pendiente-intersección.

Como hemos visto antes, puedes escribir la ecuación de cualquier recta en forma de y = mx + b. Es la llamada forma pendiente-intersección porque te da dos datos importantes: la pendiente m y la intersección con el eje Y b de la recta (también se suele emplear el término "ordenada al origen" para referirse a esta intersección). Más adelante podrás utilizar estos valores para una interpolación lineal.

La pendiente es la inclinación de una recta. Nos dice cuánto cambia y para un cambio dado en x. Si es positiva, los valores de y aumentan al aumentar x. Si es negativa, y disminuye al aumentar x. Puedes obtener más información en la descripción de nuestra calculadora de la pendiente de una recta.

La ordenada al origen es el valor de y en el que la recta cruza el eje Y. Para hallarla, tienes que sustituir x = 0 en la ecuación lineal. Más adelante verás por qué la intersección con el eje Y es un parámetro importante en las ecuaciones lineales, y también conocerás el significado físico de su valor en ciertos ejemplos del mundo real.

¿Aún necesitas saber cómo hallar la forma pendiente-intersección de una ecuación lineal? Supondremos que conoces dos puntos por los que pasa la recta. El primero tendrá coordenadas (x₁, y₁) y el segundo (x₂, y₂). Tus incógnitas serán la pendiente m y la ordenada al origen b.

En primer lugar, sustituye las coordenadas de los dos puntos en la ecuación pendiente-intersección:

(1) y₁ = mx₁ + b

(2) y₂ = mx₂ + b

Luego, resta la primera ecuación de la segunda:

y₂ - y₁ = m(x₂ - x₁)

Por último, divide ambos lados de la ecuación por (x₂ - x₁) para hallar la pendiente:

m = (y₂ - y₁)/(x₂ - x₁)

Una vez hallada la pendiente, puedes sustituirla en la primera o segunda ecuación para hallar la intersección y:

y₁ = x₁(y₂ - y₁)/(x₂ - x₁) + b

b = y₁ - x₁(y₂ - y₁)/(x₂ - x₁)

Esta calculadora de la forma pendiente-intersección te permite encontrar la ecuación de una recta en la forma pendiente-intersección. Solo necesitas brindar dos puntos por los que pasa la recta. Para eso, sigue el procedimiento que se indica a continuación.

1. Escribe las coordenadas del primer punto. Supongamos que es un punto con x₁ = 1 e y₁ = 1.

2. Escribe también las coordenadas del segundo punto. Tomemos un punto con x₂ = 2 e y₂ = 3.

3. Utiliza la fórmula de la pendiente para hallar la pendiente:

   m = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2.

4. Calcula la intersección con el eje Y. Aquí también puedes utilizar x₂ e y₂ en lugar de x₁ e y₁.

   b = y₁ - mx₁ = 1 - 2×1 = -1

5. Junta estos valores para construir la forma pendiente-intersección de una ecuación lineal:

   y = 2x - 1.

6. También puedes usar la calculadora de distancia para hallar la distancia entre dos puntos.

También es posible encontrar la intersección en X de una recta. Es el valor de x en el que la recta cruza el eje X (el valor de x para el que y es igual a 0). Puedes calcularlo de la siguiente manera:

0 = mx + b

x = -b/m

Como vemos, la única condición que debe cumplirse es que el coeficiente m sea distinto de cero.

Nuestra calculadora de la forma pendiente-intersección te mostrará los valores de la intersección en X y de la intersección en Y. Aun así, si quieres aprender más, te recomendamos que visites nuestra calculadora de intersección con el eje Y 🇺🇸.

Hemos visto qué es la forma pendiente-intersección, pero para entender por qué es tan útil, debes conocer algunas aplicaciones que tiene en el mundo real. Veamos un par de ejemplos. Empezaremos con unos sencillos ejemplos de física para que puedas hacerte una idea de lo que significan las intersecciones con los ejes X e Y.

Imagina un automóvil que se mueve a una velocidad fija hacia ti. Su movimiento puede graficarse como tiempo vs. la distancia entre el vehículo y tú (como se muestra arriba). Esto significa que el eje X representará el tiempo transcurrido, y el eje Y representará la distancia al automóvil. Incluso puedes imaginar que el automóvil ha empezado a moverse antes de que pusieras en marcha el cronómetro (es decir: antes de que t = 0).

Ahora bien, si te fijas en la intersección con el eje Y (x = 0), el punto en el que empezaste a llevar la cuenta del tiempo es t = 0. Por tanto, el valor de y en este punto indicará la posición inicial (distancia) del automóvil respecto a ti. Este valor es, como hemos dicho antes, el mismo que el valor de b en la forma pendiente-intersección de una ecuación lineal.

Observando ahora la intersección con el eje X (y = 0), este será el punto en el que la distancia del automóvil a ti será 0. Entonces el valor de x en este punto será el momento en que tú y el automóvil se encuentren en el mismo lugar. Esperemos que esto signifique que estás dentro del automóvil y no debajo.

El ejemplo del automóvil anterior es muy sencillo y te ayudará a entender por qué es importante la forma pendiente-intersección y, más concretamente, el significado de las intersecciones. En este artículo hablaremos principalmente sobre rectas, pero los puntos de intersección pueden calcularse para cualquier tipo de curva (si cruza algún eje).

De hecho, el ejemplo anterior no se ajusta a una ecuación lineal y sigue las dos intersecciones.

Una ecuación que tiene garantizada una intersección en Y, pero no necesariamente una intersección en X, es una parábola. Esta ecuación se encuentra graficada en la imagen de arriba. Tiene un máximo o un mínimo (según la orientación). Si este máximo está por debajo del eje X o el mínimo está por encima del eje X, nunca habrá una intersección con el eje X.

Sin embargo, a diferencia de los humanos, no todas las ecuaciones son iguales. Algunas de las fórmulas describen curvas que pueden no interceptar nunca el eje X, el eje Y o ambos. Veamos con un poco más de detalle cómo puede ser esto.

Podemos distinguir 3 grupos de ecuaciones según tengan solo intersección en Y, solo intersección en X, o ninguna de las dos. El primer grupo (solo intersección con el eje Y) puede tener casi cualquier tipo de ecuación, incluidas las ecuaciones lineales. Un ejemplo fácil es y = 3 (o cualquier otro valor constante de y excepto 0), ya que se trata de una recta paralela al eje X y, por el contrario, nunca cruzará este eje. Por favor, no intentes calcular este tipo de intersecciones en esta calculadora de forma pendiente-intersección, ya que este tipo de ecuaciones pueden potencialmente romper Internet.

El segundo y el tercer grupo de ecuaciones son un poco más complicados de imaginar y, para entenderlos bien, necesitamos introducir el concepto de asíntota. Una asíntota es una recta (que puede expresarse como una ecuación lineal) a la que la función o curva de la que estamos hablando se acerca cada vez más, pero que en realidad nunca cruza ni toca.

La definición puede no parecer del todo clara, pero con una ecuación de ejemplo, tendremos menos problemas para entenderla. Tomemos la ecuación y = 1/x. Si intentamos encontrar la intersección en Y sustituyendo x = 0, llegamos a lo que se llama una expresión matemáticamente indefinida, ya que no tiene sentido dividir por 0.

Si tomamos valores cada vez más cercanos a 0 (algo así como 0.1, luego 0.001, 0.000001...), vemos que el valor de y aumenta muy rápidamente. Así que alrededor del punto x = 0, sabemos que y tendría un valor enorme, pero debido a cómo funcionan las matemáticas, no tiene un valor definido para ese punto exacto. A veces la gente puede decir 1/0 = ∞, pero la realidad es que el infinito no es un número, sino un concepto.

En este caso, la ecuación lineal x = 0 representa la asíntota de la función y = 1/x, lo que significa que y = 1/x nunca cruzará esa recta y, por tanto, no tendrá intersección en Y. En general, siempre que una función tenga una asíntota que esté sobre uno de los ejes, le faltará al menos uno de los puntos de intersección.

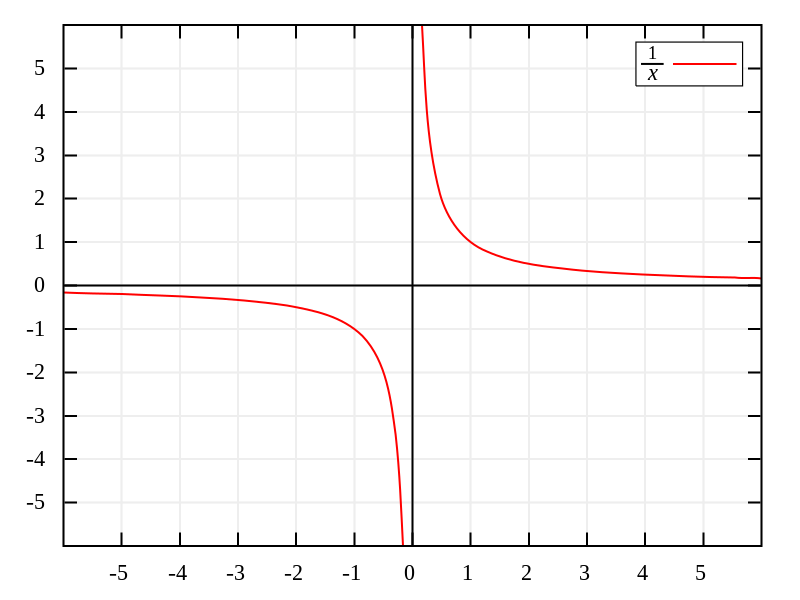
De hecho, el ejemplo que te hemos mostrado (y = 1/x) también tiene una asíntota para y = 0, es decir, el eje X. Por la misma razón que antes, y = 0 nunca es alcanzable mediante la fórmula porque requeriría x = ∞, y como hemos dicho antes, esto es imposible.

Antes de pasar al siguiente tema, es importante señalar que hemos simplificado demasiado al hablar del infinito, pero creemos que es un buen y rápido enfoque para los que no están acostumbrados al concepto de trabajar con el infinito en matemáticas. Te recomendamos que aprendas más sobre cómo tratar con el infinito, empezando por las expresiones indefinidas en matemáticas.

Uno podría pensar fácilmente que la utilidad de las ecuaciones lineales es muy limitada debido a su simplicidad. Sin embargo, la realidad es un poco distinta. Las ecuaciones lineales son el núcleo de algunos de los métodos más potentes para resolver problemas de minimización y optimización.

Los problemas de minimización son un tipo de problema en el que se trata de encontrar la forma de hacer que una de las variables sea lo más pequeña posible. Esta variable puede ser, por ejemplo, la diferencia entre la predicción hecha por un modelo y la realidad. Este tipo de problemas son uno de los problemas más comunes y son el foco del aprendizaje automático y de los experimentos científicos.

Uno de los métodos más usuales y potentes para encontrar el valor mínimo de una ecuación o fórmula es el llamado método de Newton, que debe su nombre al genio que lo inventó. Funciona utilizando derivadas, ecuaciones lineales, e intersecciones con el eje X:

Este método consiste en elegir un valor de x para la ecuación y calcular la derivada de la ecuación en ese punto. Utilizando la derivada como pendiente de una ecuación lineal que pasa por ese punto exacto (x, y), se calcula entonces la intersección en X. Esta es una de las situaciones en las que resulta útil la forma pendiente-intersección.

Una vez calculada la intersección con el eje X, hacemos uso de ese valor de x para repetir el proceso anterior, un número determinado de veces, hasta llegar a un valor de y que sea mínimo (lo que significa que la derivada será 0). En la vida real, llegar al punto mínimo exacto no es posible en un tiempo finito, por lo que normalmente nos conformamos con un valor "suficientemente cercano".

Un ejemplo muy común es cuando se emplea el método de cuadrados mínimos para ajustar datos a una fórmula o tendencia. En este caso, el valor que queremos minimizar es la suma del cuadrado de la distancia entre la línea de tendencia y los datos, donde la distancia se calcula a lo largo de una línea perpendicular desde el punto hasta la línea de tendencia.

No, la forma estándar y la forma pendiente-intersección son dos formas distintas de describir una recta:

• La forma pendiente-intersección se escribe y = mx + b, donde m es la pendiente (inclinación) de la recta, y b es la ordenada al origen o intersección en Y, es decir, el valor en el que la recta corta al eje vertical. Por ejemplo, y = -2x + 3.
• La forma estándar es Ax + By + C = 0, donde A, B, C son números enteros. Por ejemplo, 2x + y - 3 = 0.

Si quieres reescribir tu ecuación en forma estándar a la forma pendiente-intersección, sigue estos pasos:

1. Escribe la forma estándar de la recta: Ax + By + C = 0.
2. Mueve Ax y C al lado derecho, dejando al término By en el lado izquierdo: By = -Ax - C.
3. Divide ambos lados por B: y = -(A/B)x - (C/B).
4. Como puedes ver, tenemos la forma pendiente-intersección y = mx + b con pendiente m = -A/B e intersección en Y (ordenada al origen) b = -C/B.

La pendiente describe la inclinación de una línea. La pendiente puede ser positiva, negativa o cero y:

• una pendiente positiva significa que la línea aumenta de izquierda a derecha;
• pendiente negativa significa que la línea desciende de izquierda a derecha; y
• pendiente cero significa que la línea es horizontal.

Cuanto mayor sea el valor absoluto de la pendiente, más rápido aumentará/disminuirá la línea. De hecho, el valor de la pendiente es exactamente la cantidad en que la recta aumenta/disminuye cuando x aumenta una unidad.

La pendiente es m = 1. Para llegar a este resultado, utiliza la fórmula m = tan(α), donde α es el ángulo entre la recta y el eje x. Como tan(45°) = 1, obtenemos la pendiente 1.