Calculadora de razón de cambio promedio
Table of contents
¿Qué es la razón de cambio? Definamos la tasa de variación mediaFórmula de la razón de cambio promedio¿Cómo hallar la razón de cambio promedio? Primer ejemplo¿Cómo hallar la razón de cambio promedio? Segundo ejemploFAQsLa calculadora de la razón de cambio promedio está aquí para ayudarte a comprender el sencillo concepto que se esconde tras un nombre largo y un poco confuso. ¿Qué es la razón de cambio, también conocida como “tasa de variación”? En términos generales, muestra la relación entre dos factores. A continuación encontrarás una definición más precisa de la razón de cambio promedio. También demostraremos y explicaremos la fórmula de la razón de cambio promedio con un par de ejemplos de cómo utilizarla.
¿Prefieres ver a leer? Aprende todo lo que necesitas en 90 segundos con este vídeo que hemos hecho para ti:
¿Qué es la razón de cambio? Definamos la tasa de variación media
Todo se mueve. El cambio es inevitable. Desde la aceleración de tu bicicleta o automóvil hasta el crecimiento de la población, desde el flujo sanguíneo de tus venas hasta la simbiosis de tus células, la razón de cambio nos permite establecer el valor asociado a esos cambios.
La razón de cambio promedio, o tasa de variación media, es una tasa o razón que describe cómo cambia un número, en promedio, con relación con otro. Si tienes una función, es la pendiente de la recta trazada entre dos puntos. Pero no la confundas con la pendiente de la función en cada punto. Puedes utilizar la razón de cambio promedio para cualquier función, no solo las lineales.
🙋 Si quieres saber más sobre la pendiente, ve a la calculadora de pendientes.
Fórmula de la razón de cambio promedio
En la imagen siguiente, hemos marcado dos puntos para ayudarte a comprender mejor cómo hallar la razón de cambio promedio.
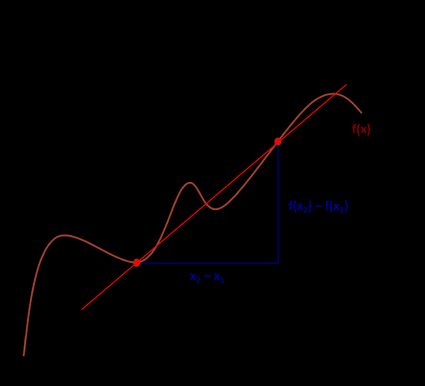
La fórmula de la razón de cambio promedio es:
A = [f(x₂) - f(x₁)] / [x₂ - x₁]
donde:
- (x₁, f(x₁)) - Coordenadas del primer punto.
- (x₂, f(x₂)) - Coordenadas del segundo punto.
Si es positiva, significa que una coordenada aumenta a medida que la otra también aumenta. Por ejemplo, cuanto más montes en bici, más calorías quemarás.
Es igual a cero cuando una coordenada cambia pero la otra no. Un buen ejemplo podría ser no estudiar para los exámenes. Cuando el tiempo empieza a correr, la cantidad de cosas que hay que aprender no cambia.
La razón de cambio promedio es negativa cuando una coordenada aumenta mientras que la otra disminuye. Supongamos que te vas de vacaciones. Cuanto más tiempo dediques al viaje, más cerca estarás de tu destino.
💡 Puedes aprender otras formas de describir la diferencia entre dos puntos en la calculadora de la altura y horizontal de una pendiente 🇺🇸.
¿Cómo hallar la razón de cambio promedio? Primer ejemplo
Calculemos la razón de cambio promedio de la distancia (velocidad media) de un tren que va de París a Roma (1420.6 km). En el siguiente gráfico, puedes ver la variación de la distancia a lo largo del tiempo:
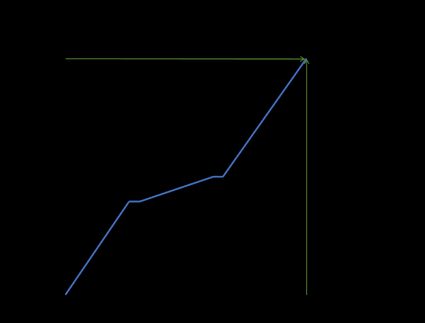
Como ves, la velocidad no era constante. El tren se detuvo dos veces y, entre parada y parada, iba bastante más despacio. Pero para calcular la velocidad media, las únicas variables que importan son el cambio en la distancia y el cambio en el tiempo. Así pues, si las coordenadas del primer punto son (0, 0), y las coordenadas del segundo punto son la distancia entre dos ciudades, y el tiempo de viaje es (1420.6, 12.5), entonces:
A = (1420.6 - 0) / (12.5 - 0) = 113.648 [km/h]
En promedio, el tren iba a 113.648 kilómetros por hora. Veamos ahora un ejemplo más matemático.
¿Cómo hallar la razón de cambio promedio? Segundo ejemplo
Se te ha asignado una función:
f(x) = x² + 5x - 7
Halla la razón de cambio promedio en el intervalo [-4, 6].
-
Halla los valores de tu función para ambos puntos:
f(x₁) = f(-4) = (-4)² + 5 × (-4) - 7 = -11
f(x₂) = f(6) = 6² + 5 × 6 - 7 = 59
-
Utiliza la ecuación de la razón de cambio promedio:
A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11)] / [6 - (-4)] = 70 / 10 = 7
Si te ha gustado la calculadora de la razón de cambio promedio, no dudes en consultar nuestras otras herramientas, como esta calculadora de distancias, donde puedes hallar la distancia entre puntos o rectas.
¿Es la razón de cambio promedio lo mismo que la pendiente?
Técnicamente, no. La razón de cambio promedio refleja cómo varía una función, en promedio, entre dos puntos. En cambio, definimos la pendiente de una función como la pendiente de la recta tangente a la curva en un punto concreto. En una función lineal, cada punto cambia de forma idéntica, por lo que la razón de cambio promedio y la pendiente son iguales.
¿Cómo hallas la razón de cambio promedio de una función?
Para hallar la razón de cambio promedio de una función, sigue estos pasos:
-
Obtén las coordenadas (x, y) del punto inicial. Las llamaremos (x₀, y₀).
-
Obtén las coordenadas (x, y) del punto final. Serán (x₁, y₁).
-
Sustituye ambas dentro de la fórmula de la razón de cambio promedio (A):
A = (y₁ - y₀)/(x₁ - x₀).
¿Cuál es la razón de cambio promedio de y = 2x?
La razón de cambio promedio de y = 2x es 2. Como se trata de una función lineal, la razón de cambio promedio no es más que la pendiente de la función. En este caso, por cada cambio en la coordenada x, la coordenada y la duplicará.
¿Es la velocidad un ejemplo de razón de cambio promedio?
Si la velocidad es constante, sí. La velocidad refleja cómo cambia la posición instantáneamente con respecto al tiempo. Por tanto, si un objeto se moviera a velocidad constante, la razón de cambio promedio de la posición nos diría a qué velocidad se desplaza.