Calculadora de perímetro
Con esta calculadora de perímetro ya no tendrás que preocuparte por hacer los cálculos de perímetro. A continuación encontrarás las fórmulas de perímetro para doce figuras geométricas diferentes, así como un breve recordatorio sobre qué es el perímetro de una figura, cómo se saca el perímetro y una definición de perímetro. Sigue leyendo, pruébala, o consulta a la hermana gemela de esta calculadora: nuestra completa calculadora de área.
¿Qué es el perímetro de una figura?
El perímetro es la frontera de una figura geométrica cerrada. También puede definirse como el borde exterior de un área, simplemente la línea continua más larga que rodea a una figura. La respuesta sobre qué es el perímetro también se encuentra en su propio nombre. “Perímetro” procede del griego perimetros: peri, que significa “alrededor” + metron, entendido como “medida”. Ya que el perímetro es la longitud del contorno de la figura, este se expresa en unidades de distancia: por ejemplo, metros, pies, pulgadas o millas.
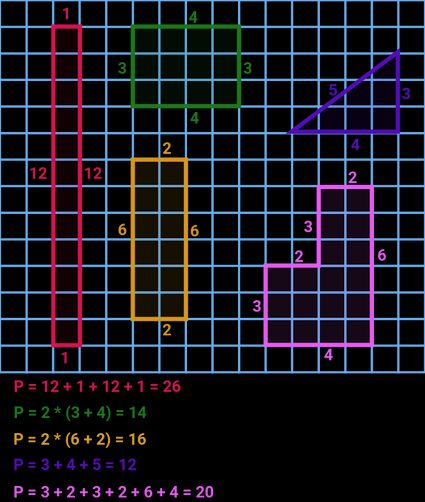
Cómo se saca el perímetro: fórmulas de perímetro
Ahora que ya sabemos qué es el perímetro, podemos pasar a la próxima pregunta: cómo se saca el perímetro, o sea, cómo calcular el perímetro. Normalmente, lo más sencillo y directo será encontrar la suma de todos los lados de una figura. Sin embargo, habrá casos en los que no haya lados (elipses, círculos, etc.), o se desconozcan uno o más lados. En este apartado enumeraremos todas las ecuaciones utilizadas en esta calculadora de perímetro.
Desplázate a las secciones siguientes si tienes curiosidad sobre una forma concreta y deseas ver una explicación, una derivación, o una imagen de cada una de las doce formas presentes en esta calculadora. Caso quieras más información sobre cómo se saca el perímetro de una figura específica, disponemos de herramientas dedicadas a cada figura por separado: solo tienes que escribir el nombre de la figura en la barra de búsqueda de la parte superior de esta página web.
Aquí tienes las fórmulas para el perímetro de las doce figuras geométricas de esta calculadora:
-
fórmula del perímetro de un cuadrado: .
-
fórmula del perímetro de un rectángulo: .
-
fórmulas para el perímetro de un triángulo:
-
-
-
.
-
-
fórmula del perímetro de un círculo: .
-
fórmula del perímetro del sector circular: ( se ingresa en radianes).
-
fórmula del perímetro de una elipse: .
-
fórmula del perímetro de un cuadrilátero/trapecio: .
-
fórmulas para el perímetro de un paralelogramo:
-
-
fórmulas para el perímetro de un rombo:
-
-
.
-
-
fórmula del perímetro de un deltoide o cometa: .
-
fórmula del perímetro de una corona circular: .
-
fórmula del perímetro de un polígono regular: .
Fórmula del perímetro de un cuadrado

Un cuadrado tiene cuatro lados de igual longitud. Para calcular su perímetro, basta con multiplicar la longitud de los lados por :
Lo creas o no, ¡también tenemos una calculadora del perímetro de un cuadrado 🇺🇸!
Fórmula del perímetro de un rectángulo

La fórmula del perímetro de un rectángulo es casi tan fácil como la ecuación del perímetro de un cuadrado. La única diferencia es que ahora tenemos dos pares de lados de igual longitud:
Fórmula del perímetro de un triángulo

La forma más sencilla de calcular el perímetro de un triángulo 🇺🇸 es, como siempre, sumar todos los lados:

Sin embargo, no siempre te darán las tres caras. ¿Qué puedes hacer entonces? Bueno, en lugar de preocuparte, puedes utilizar la calculadora de la ley del coseno 🇺🇸 para encontrar el lado que falta:
puede incorporarse a la fórmula del perímetro:

La otra opción es utilizar la ley de los senos si tienes un lado y los dos ángulos que tocan dicho lado:
Y:
Por lo que el perímetro del triángulo puede expresarse como
Fórmula del perímetro de un círculo (fórmula de la longitud de una circunferencia)

El "perímetro de un círculo" es la longitud de la circunferencia que forma dicho círculo. La fórmula más conocida del perímetro de un círculo utiliza una sola variable: su radio
¿Te has preguntado alguna vez cuántas veces girará la rueda de tu bicicleta en un recorrido de 16 kilómetros? Pues ese es uno de los casos en los que necesitarás utilizar la fórmula del perímetro de un círculo. En la fórmula de arriba, introduce el radio de tu rueda (la mitad del diámetro de la rueda), y divide 16 kilómetros por el perímetro obtenido (¡pero no te olvides de la conversión de las unidades de longitud!). Si quieres ser aún más preciso, puedes incluir el tamaño del neumático de la bicicleta.
Fórmula del perímetro de un sector circular

Calcular el perímetro de un sector circular puede parecer complicado: ¿es solo la longitud del arco, o es la longitud del arco más dos radios? ¡Solo debes tener en cuenta la definición de perímetro! El perímetro del sector es la suma de las longitudes de todas sus fronteras, por lo que usamos la longitud del arco más los dos radios
Donde se ingresa en radianes.
Fórmula del perímetro de una elipse

Aunque la fórmula del área de una elipse es realmente sencilla y fácil de recordar, la fórmula del perímetro de una elipse es la más problemática de todas las ecuaciones que aparecen aquí. En esta calculadora de perímetros, hemos optado por aplicar una de las aproximaciones de Ramanujan:
Donde es el radio más corto posible y es el radio más largo posible de una elipse. La otra aproximación de Ramanujan, más exacta, es:
También existe una forma más sencilla: utilizando una variable adicional :
Es decir:
o también puedes utilizar nuestra calculadora ;)
Fórmula del perímetro de un trapecio

Si quieres saber cómo calcular el perímetro de un trapecio irregular, no hay ninguna fórmula especial, simplemente suma los cuatro lados:
Quizá te hayas dado cuenta, pero es la fórmula del perímetro de cualquier cuadrilátero.
También hay una opción que se presenta con ciertos trapecios especiales, como el trapecio isósceles, en el que necesitas los lados , y . Otro ejemplo es el trapecio rectángulo, en el que la longitud de las bases y de un cateto son suficientes para hallar el perímetro de la figura (para hallar el último cateto, usamos el teorema de Pitágoras).
Fórmula del perímetro de un paralelogramo

En esta calculadora de perímetro encontrarás tres fórmulas para calcular el perímetro de un paralelogramo:
- La más sencilla, sumando todos los lados:

- La fórmula del perímetro de un paralelogramo que requiere un lado y diagonales

- Cuando el perímetro se da en términos de base, altura y cualquier ángulo del paralelogramo.
Fórmula del perímetro de un rombo

La fórmula del perímetro de un rombo no es ingeniería aeroespacial, así que hagámosla concisa: ¡es la misma que la fórmula del perímetro de un cuadrado!

La otra solución para hallar el perímetro del rombo requiere las longitudes de las diagonales:
Intenta derivar tú mismo la fórmula. Sabes que las dos diagonales de un rombo son perpendiculares y se bisecan entre sí, de modo que puedes dividir la figura en cuatro triángulos rectángulos congruentes. Como cada triángulo tiene catetos que miden e/2 y f/2, lo único que tienes que hacer es hallar la hipotenusa del triángulo, que es, al mismo tiempo, el lado del rombo. Luego multiplica el resultado por cuatro para hallar la fórmula final del perímetro de un rombo.
Fórmula del perímetro de un deltoide o cometa

La fórmula del perímetro de un deltoide es bastante sencilla: basta con sumar todos los lados:
Fórmula del perímetro de una corona circular

Puesto que el perímetro se define como la frontera, una corona circular requiere que sumemos la circunferencia de ambos círculos concéntricos:
Fórmula del perímetro de un polígono (pentágono regular, hexágono, octógono, etc.)

En nuestra calculadora de perímetro, también hemos implementado una fórmula sencilla para el perímetro de un polígono regular:
donde es el número de lados del polígono. Así, por ejemplo, puedes calcular el perímetro de un pentágono, un hexágono o un octógono.
Además, para polígonos de hasta 12 lados, el nombre del polígono aparecerá en la herramienta. ¡Fantástico!
Si quieres determinar el perímetro de cualquier polígono, suma las longitudes de todos sus lados:
donde , , ..., son las longitudes de los lados, y es el símbolo de suma (de a ).
O utiliza las coordenadas de los vértices:
Con and .
Preguntas frecuentes
¿Cómo calculo el perímetro de figuras geométricas irregulares?
Para calcular el perímetro de figuras geométricas irregulares:
- Mide las longitudes de todos los lados (exteriores).
- Si los lados incluyen fragmentos circulares, mide el radio y el ángulo central, es decir, el ángulo entre los radios que unen a los dos puntos finales del arco con el centro.
- Aplica la fórmula del perímetro de un círculo para este radio, y toma la parte proporcional al ángulo.
- Suma la longitud de todos los lados.
¿Puedo determinar el área dado el perímetro?
En general, no, no es posible calcular el área a partir del perímetro. Esto es especialmente cierto en el caso de los rectángulos, paralelogramos, cometas, y trapecios. Sin embargo, para algunas figuras geométricas concretas, como cuadrados, hexágonos, polígonos regulares en general, y círculos, puedes determinar su lado (o radio, en el caso de los círculos) a partir del perímetro y luego proceder a calcular el área.
¿Cuál es el perímetro de un edificio rectangular de 20 m por 15 m?
El perímetro es de 70 m. Para llegar a este resultado, tienes que sumar la longitud de los cuatro lados del edificio. Dos lados de 20 m de longitud sumados dan 40 m, mientras que los otros dos lados de 15 m de longitud sumados dan 30 m. Juntos, obtenemos 40 m + 30 m = 70 m, como se dijo.