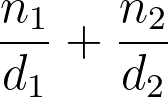Te damos la bienvenida a nuestra calculadora de fracciones, una herramienta realmente versátil que puede hacer:
- ➕ sumas de fracciones;
- ➖ restas de fracciones;
- ✖️ multiplicaciones de fracciones; y
- ➗ divisiones de dos fracciones cualesquiera.
Además, tiene la capacidad de simplificar una fracción (reducir), así como de decirte cómo convertir una fracción en un decimal, y viceversa. Si todavía no estás impresionado, esta calculadora de fracciones no solo funciona con fracciones propias e impropias, sino también con fracciones mixtas, ¿qué más se puede pedir? 😁
Como de costumbre, hemos preparado textos introductorios, que te permitirán adentrarte en el mundo de las fracciones 🌎. A continuación leerás sobre la definición de fracción, los tipos de fracciones (propias, impropias y mixtas) y todas las operaciones con fracciones básicas, como la suma y resta de fracciones. ¿Estás preparado?
¿Qué es una fracción? Definición de fracción
Una fracción representa la porción de partes iguales de algo.
Puedes reconocer una fracción simple porque tiene dos números separados por una línea (o barra):
-
Al número de arriba lo llamamos numerador y lo escribimos encima de la raya. Nos dice:
Cuántas partes tenemos.
-
Al número inferior lo llamamos denominador y lo escribimos debajo de la línea. Significa:
El número total de partes.
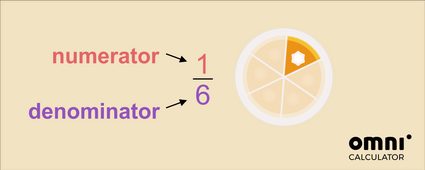
En el ejemplo anterior, es una parte de las seis porciones en que se cortó la torta en total. Lo leemos como una sexta parte de toda la torta.
Pero, por supuesto, ¡la torta se puede cortar de otras maneras!
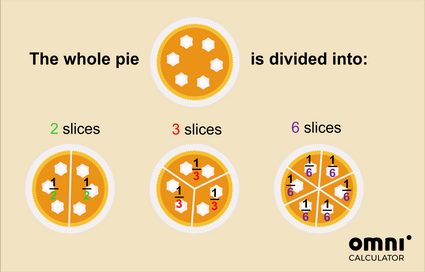
Así, si cortas el pastel en 2 partes, entonces una porción es la mitad del pastel entero. Si lo cortas en 3 partes, entonces una porción es un tercio, etc.
Utilizamos fracciones constantemente:
-
Cada vez que quieres expresar una parte de un objeto entero, que puede dividirse en trozos iguales: como un pastel 🍰, una tableta de chocolate 🍫, una sandía 🍉, una pizza 🍕, etc;
-
Cuando medimos algo 📏, especialmente en metros ("estas cortinas son 1/3 más cortas que aquellas"); y
-
El tamaño de la pantalla de tu computadora 🖥️ se expresa como una proporción, por ejemplo, 16:9, y también es una fracción, solo que se escribe de otra manera. Para saber cómo simplificar las proporciones, consulta nuestra calculadora de razones
¿Qué son fracciones propias, fracciones impropias y fracciones mixtas?
Ahora que ya conoces la definición de fracción, veamos los distintos tipos de fracciones que encontrarás en esta calculadora de fracciones. En general, tenemos tres tipos de fracciones: fracciones propias, impropias y mixtas:
-
Fracciones propias
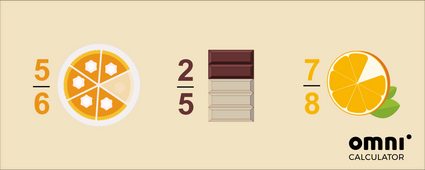
En las fracciones propias, el número superior (numerador) es menor que el número inferior (denominador). Esto significa que siempre será menor que el total de algo, por ejemplo:
🍰 5 trozos de torta de una torta que se cortó en 6;
🍫 2 partes de una barra de chocolate que tiene 5 partes; y
🍊 7 gajos de una naranja que contiene 8.
La regla general, que sirve tanto para números positivos como negativos, es que el valor absoluto de la fracción sea menor que uno:
|numerador/denominador| < 1
-
Fracciones impropias
¿Qué es una fracción impropia? Es una fracción en la que el numerador es mayor (o igual) que el denominador. Ejemplos de fracciones impropias son:
🍰 10 porciones de pastel, cuando cada pastel tiene 6 trozos;
🍫 8 partes de una barra de chocolate. Una barra de chocolate entera tiene 5 partes; y
🍊 21 gajos de naranja, cuando cada naranja tiene 8 gajos iguales.

-
Fracciones mixtas
Las fracciones mixtas, también conocidas como números mixtos o fracciones con enteros, son otra forma de expresar una fracción impropia. Se forman con números enteros (número de elementos) y una fracción propia juntos. Veamos los ejemplos del párrafo anterior:
🍰 10 trozos de pastel, cuando cada pastel tiene 6 trozos es lo mismo que → 1 pastel entero y 4 trozos de 6;
🍫 8 pedazos de chocolate, cuando toda la barra de chocolate tiene 5 partes → 1 barra de chocolate entera y 3 pedazos de un total de 5; y
🍊 21 gajos de naranja, si cortamos la naranja en 8 gajos → 2 naranjas enteras y 5 gajos de un total de 8.

💡 Las cosas más importantes que debes recordar después de leer esta sección:
- Una fracción propia tiene un numerador (número superior) menor que su denominador (número inferior);
- El numerador de una fracción impropia es mayor (o igual) que su denominador; y
- Los números mixtos, o fracciones con enteros, están formados por un número entero y una fracción propia.
Ahora que ya conoces un poco mejor los diferentes tipos de fracciones, ¿pasamos a las operaciones con fracciones?
¿Cómo hacer suma de fracciones? ➕
Cuando se trata de sumar fracciones, hay tres escenarios:
-
El denominador (número inferior) es el mismo en ambas fracciones. Por ejemplo, 3/5 y 1/5.
Este es el caso más sencillo; basta con sumar los numeradores (números superiores) y dejar el denominador como está, p. ej.:
➽ 3/5 + 1/5 = (3 + 1)/5 = 4/5
-
Las fracciones tienen denominadores distintos. Por ejemplo, 2/5 y 3/10.
Este es un caso un poco más complicado: para sumar estas fracciones, tienes que encontrar el denominador común.
-
Puedes utilizar, por ejemplo, mcm (el mínimo común múltiplo), para hallar al múltiplo común de tus dos denominadores:
mcm(5,10) = 10. Otra opción es multiplicar tus denominadores y reducir la fracción después. -
Luego, tienes que expandir cada fracción para que este denominador común sea su número inferior:
Así, debes multiplicar la fracción con el denominador igual a 5 (nuestro 1/5) por 2 para obtener 10 (recuerda que debes multiplicar tanto los números superiores como los inferiores):
➽ 2/5 = (2 × 2)/(5 × 2) = 4/10
Tu segunda fracción ya tiene su denominador igual a 10:
➽ 3/10
-
Ahora que tus fracciones tienen el mismo denominador, puedes sumarlas:
➽ 4/10 + 3/10 = (4 + 3)/10 = 7/10
-
-
Quieres encontrar la suma de fracciones mixtas. Por ejemplo, 2 3/5 y 1 1/2.
Una solución para este tipo de problema es convertir la fracción mixta en una fracción impropia y sumarla como de costumbre.
Convirtámosla en 2 3/5
-
Multiplica el número entero por el denominador:
2 × 5 = 10
-
Suma el resultado al numerador:
10 + 3 = 13
-
Ese es tu nuevo numerador: escríbelo encima de tu denominador:
2 3/5 = 13/5
Análogamente, puedes hallar que 1 1/2 = 3/2.
-
Suma, como explicamos arriba, las fracciones con distintos denominadores:
➽ 13/5 + 3/2 = 26/10 + 15/10 = 41/10
-
Por último, puedes volver a convertir tu resultado en una fracción mixta:
Realiza una división larga con resto:
➽ 41/10 = 4 R 1 = 4 1/10
-
Por supuesto, nuestra calculadora de fracciones puede resolver esta suma de fracciones mixtas, así como todos los demás ejemplos. 😎
Si todavía te preguntas sobre cómo hacer sumas de fracciones, ¿quizá una imagen te ayude?
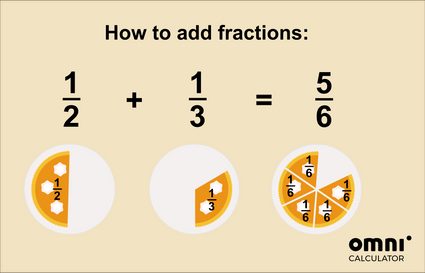
Para una explicación aún más detallada, consulta nuestra calculadora de suma de fracciones 🇺🇸.
¿Cómo hacer resta de fracciones? ➖
Si te preguntas cómo hacer resta de fracciones y has leído la sección anterior Cómo hacer suma de fracciones, tenemos buenas noticias para ti: ¡es prácticamente lo mismo!
-
Si tienes fracciones con el mismo denominador, resta los numeradores:
➽ 3/5 - 1/5 = (3 - 1)/5 = 2/5
-
Cuando hagas la resta de fracciones con diferentes denominadores, como 2/5 y 3/10, repite el procedimiento del apartado anterior, pero restando, no sumando en el paso final:
-
Encuentra un denominador común: en este caso, 10.
-
Expande las fracciones a sus fracciones equivalentes utilizando el denominador común: 4/10 y 3/10.
-
Resta los numeradores.
➽ 2/5 - 3/10 = 4/10 - 3/10 = 1/10
-
-
Para fracciones mixtas (23/5 y 1 1/2):
-
Cambia las fracciones mixtas por fracciones impropias, como antes:
2 3/5 = 13/5 y 1 1/2 = 3/2
-
Haz la resta de las fracciones impropias con diferentes denominadores:
➽ 13/5 - 3/2 = 26/10 - 15/10 = 11/10
-
Escríbelo como fracción impropia, o conviértelo de nuevo en una fracción mixta:
➽ 11/10 = 1 R 1 = 1 1/10
-
Puedes imaginar la resta como tomar o comer parte del pastel:
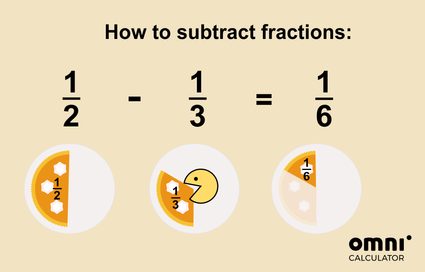
La resta de fracciones no es tan difícil, ¿verdad? Aún más cuando utilizas este maravilloso resolvedor de fracciones.
¿Cómo hacer multiplicación de fracciones? ✖️ Reglas para multiplicar fracciones
Ahora que ya sabes hacer la suma y resta de fracciones, aprender a multiplicar fracciones será sumamente sencillo. Para realizar esta operación, se multiplican numerador con numerador y denominador con denominador. A veces también hay que llegar a fracciones simplificadas para resolver la ecuación.
Mira este ejemplo:
➽ 2/3 × 5/6 = (2 × 5)/(3 × 6) = 10/18
que luego puedes simplificar a 5/9
Siempre que trates con fracciones mixtas, no olvides que siempre debes escribirlas como una fracción impropia antes de multiplicar las fracciones:
➽ 2 1/2 × 3 1/4 = 5/2 × 13/4 = (5 × 13)/(2 × 4) = 65/8 = 8 1/8
Y cuando multipliques una fracción por un número entero, recuerda que puedes escribir el número entero como él mismo dividido por 1:
➽ 3 × 5/7 = 3/1 × 5/7 = (3 × 5)/(1 × 7) = 15/7
Si no sabes qué son las fracciones simplificadas o cómo reducir fracciones, desplázate hasta la sección Cómo simplificar fracciones.
Ahora que ya sabes cómo hacer multiplicación de fracciones, pasemos al siguiente tema, la división de fracciones.
¿Cómo hacer divisiones de fracciones? ➗
¿Te torturas pensando cómo dividir fracciones? ¡No te preocupes! La división de fracciones es bastante similar a la multiplicación de fracciones. La única diferencia es que debes multiplicar la primera fracción por el recíproco de la segunda fracción. Puede sonar un poco raro, ¡pero es muy sencillo! Echa un vistazo a este ejemplo:
(1/2) / (3/5) = 1/2 × 5/3 = (1 × 5)/(2 × 3) = 5/6
Por tanto, lo único que tienes que hacer es dar la vuelta a la segunda fracción (eso significa su recíproco) y multiplicar normalmente las fracciones resultantes. A veces, puede que también necesites hacer alguna simplificación de fracciones. ¡Y eso es todo! 🎉
¿Cómo simplificar fracciones?
Nos gustan las cosas sencillas, incluso en matemáticas. Por eso es tan importante simplificar las fracciones. Simplificar, aquí, significa que escribimos la fracción en su forma más simple posible. También llamamos a las fracciones simplificadas como fracciones en forma reducida.
Pero, ¿qué significa esto exactamente? Echa un vistazo a estos ejemplos:
- Suena mejor decir que queda un cuarto de pizza, en vez de dos octavos, ¿verdad?
- O que se han comido la mitad de un pastel, en lugar de tres sextos.
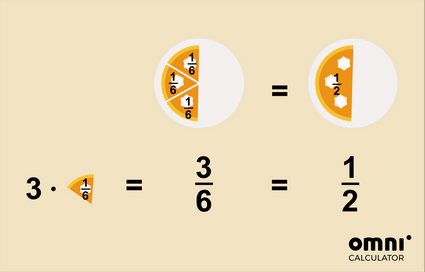
Para simplificar una fracción, puedes utilizar dos métodos:
-
Utiliza una especie de método de fuerza bruta: divide la fracción por 2, 3, 5, 7, 11... hasta que sea imposible continuar la división (sin resto):
➽ 42/126 = /:2
➽ 21/63 = /:3
➽ 7/21 = /:7
➽ 1/3
-
Halla el MCD (máximo común divisor) del numerador y el denominador, y luego divídelos por este número:
MCD(42,126) = 42, por lo que:➽ 42/126 = /:42
➽ 1/3
Lee más sobre reducción de fracciones en nuestra calculadora para simplificar fracciones 🇺🇸. Además, asegúrate de echar un vistazo a nuestra increíble calculadora de fracciones equivalentes 🇺🇸, que puede hallar las distintas maneras en las que puedes escribir una fracción.
¿Cómo convierto un decimal en fracción?
Si quieres averiguar cómo convertir un decimal en una fracción, estás en el lugar adecuado. Aquí tienes una guía paso a paso:
Supongamos que quieres convertir 0.32 en una fracción:
-
Trata tu decimal como numerador, siendo 1 el denominador.
-
Desplaza el punto decimal hacia la derecha, hasta que solo tengas un número entero:
0.32 → 3.2 → 32
Cada movimiento corresponde a una multiplicación por 10
0.32 × 10 → 3.2 × 10 → 32
-
Has multiplicado el numerador por 10 × 10, y ahora tenemos que multiplicar el denominador por el mismo número:
1 × 10 × 10 = 100
-
¡Has cambiado la fracción por un decimal! ✨ 0.32 → 32/100
-
Por último, simplifica el resultado. Como el máximo común divisor de 32 y 100 es 4, divide tanto el numerador como el denominador por este valor:
➽ 32/100 = 8/25
Y ya está, ahora tienes la fracción en su forma más simple. ❤️ Por supuesto, también lo puedes hacer todo con nuestro resolvedor de fracciones.
¿Cómo convierto una fracción en decimal?
Pues bien, la forma más fácil de convertir una fracción en decimal es... utilizar una calculadora. Ya sea esta calculadora de fracciones, una calculadora de bolsillo estándar o nuestra herramienta dedicada: el convertidor de fracciones a decimales 🇺🇸.
A veces la fracción es relativamente fácil de convertir en decimal sin ninguna herramienta, como para 1/2, 3/4 (o incluso 1/8). Creemos que puedes expandir las fracciones anteriores para que tengan 10, 100, 1000, etc. en el denominador, respectivamente:
-
Multiplica 1/2 por 5 para obtener 10 como denominador:
➽ 1/2 = 5/10 = 0.5
-
Multiplica 3/4 por 25 para obtener 100 como denominador:
➽ 3/4 = 75/100 = 0.75
-
Multiplica 1/8 por 125 para obtener 1000 como denominador:
➽ 1/8 = 125/1000 = 0.125
Pero, ¿y si no tienes Internet ni una calculadora a mano, sino solo papel y lápiz 📝? ¿Y si, además, tu fracción no parece tan fácil de expandir como las anteriores? Entonces, probablemente tendrás que hacer la división larga a mano. ¡Suerte! 🤞
Preguntas frecuentes
¿Cómo hacer sumas de fracciones con diferentes denominadores?
Primero tienes que encontrar un denominador común. Utilizaremos 1/2 y 3/5 como ejemplo. Sigue estos pasos para hacer la suma de fracciones con diferentes denominadores:
-
Encuentra el mínimo común múltiplo (mcm) del denominador:
10
-
Divide el mcm por cada denominador y multiplica a los numeradores por cada resultado:
-
10/2 = 5
5 × 1 = 5 -
10/5 = 2
2 × 3 = 6
-
-
Suma los números hallados en el paso 2 y coloca la respuesta como numerador:
-
6 + 5 = 11
-
11/10 = 1 1/10
-
-
¡Perfecto! Has sumado fracciones con denominadores diferentes.
¿Son las fracciones números racionales?
Sí, toda fracción es un número racional, pero no todos los números racionales son fracciones. Un número racional es una fracción solo cuando el numerador y el denominador son números enteros.
¿Cómo escribo 0.3333 como fracción?
0.3333 escrito como fracción es 3333/10000.
Para hallar esta respuesta:
-
Escribe el decimal como numerador y 1 como denominador:
0.3333/1
-
Mueve el punto decimal a la derecha al final del número para que aparezca como un entero:
3333
-
Agrega al denominador el mismo número de ceros que el número de posiciones que has desplazado el punto decimal. En este caso, son cuatro:
10000
-
Coloca el número del Paso 2 como numerador y el número del Paso 3 como denominador:
3333/10000
¿Cuál es el producto de 1/2 y 5/3?
El producto de 1/2 y 5/3 es 5/6.
Para llegar a esta respuesta, multiplicamos los numeradores y denominadores por separado:
-
1 × 5 = 5; y
-
2 × 3 es 6; por tanto,
-
1/2 × 5/3 = 5/6.