Calculadora del círculo unitario

Bienvenido a la calculadora del círculo unitario ⭕. Nuestra herramienta te ayudará a determinar las coordenadas de cualquier punto del círculo unitario. Sólo tienes que introducir el ángulo ∡, y te mostraremos el seno y coseno de tu ángulo.

Si no estás seguro de qué es un círculo unitario, desplázate hacia abajo y encontrarás la respuesta. La ficha del círculo unitario y una explicación sobre cómo hallar la tangente del círculo unitario, el seno y el coseno también están aquí, así que no esperes más: ¡sigue leyendo en esta calculadora de trigonometría fundamental!

Un círculo unitario es un círculo de radio 1 (radio unitario). En la mayoría de los casos, está centrado en el punto $(0,0)$, el origen del sistema de coordenadas.

El círculo unitario es un concepto muy útil para aprender trigonometría y conversión de ángulos.

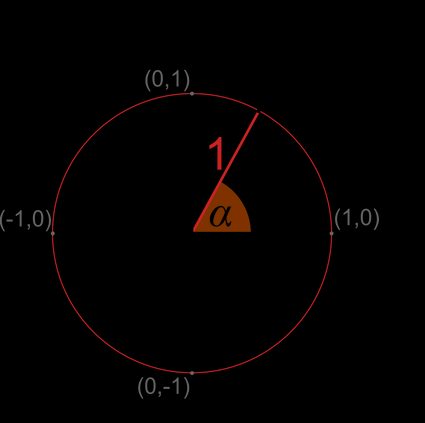
Ahora que ya sabes lo que es un círculo unitario, pasemos a las relaciones en el círculo unitario.

Bien, ¿por qué es tan útil el círculo unitario en trigonometría?

En resumen:

Relaciones del círculo unitario para el seno y el coseno:

• El seno es la coordenada y;
• El coseno es la coordenada x

Explicación estándar:

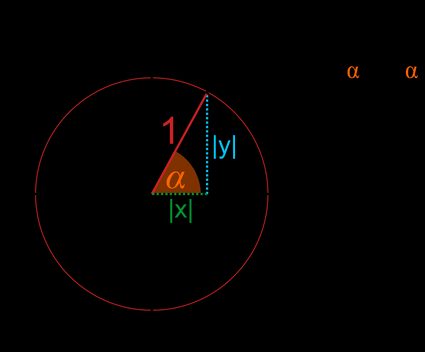
Tomemos un punto A cualquiera de la circunferencia del círculo unitario.

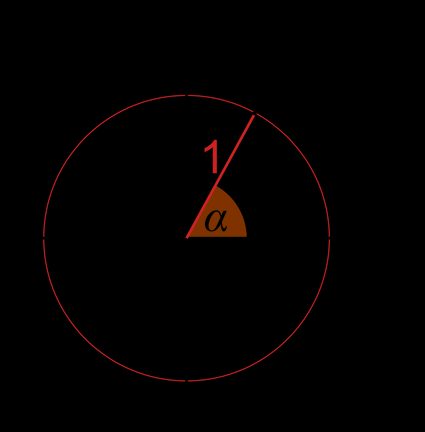
• Las coordenadas de este punto son $x$ y $y$. Como se trata de un círculo unitario, el radio r es igual a $1$ (distancia entre el punto $P$ y el centro del círculo).

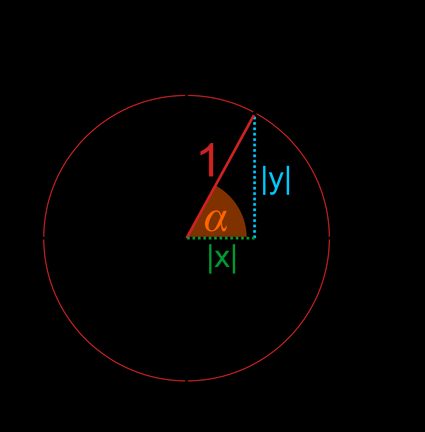
• Proyectando el radio sobre los ejes x e y, obtendremos un triángulo rectángulo, donde $|x|$ y $|y|$ son las longitudes de los catetos, y la hipotenusa es igual a $1$.

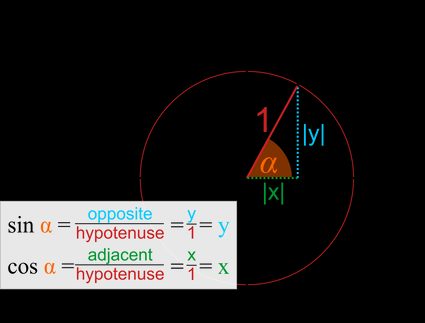
• Como en todo triángulo rectángulo, puedes determinar los valores de las funciones trigonométricas hallando las razones de los lados:

En otras palabras, el seno es la coordenada y.

Y el coseno es la coordenada x.

La ecuación del círculo unitario, que procede directamente del teorema de Pitágoras, es la siguiente:

O, análogamente:

¡Esta íntima conexión entre trigonometría y triángulos no puede ser más sorprendente! Encuentra más información sobre estos importantes conceptos en la calculadora de triángulo rectángulo de Omni.

Puedes hallar directamente el valor de la tangente del círculo unitario si recuerdas la definición de tangente:

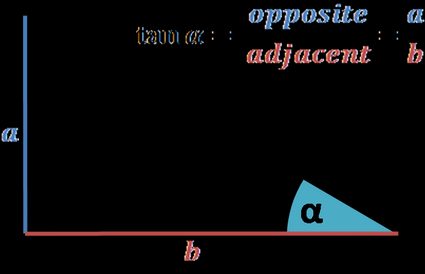
Relación entre los lados opuestos y adyacentes de un ángulo en un triángulo rectángulo.

Como hemos aprendido en el párrafo anterior, $\text{sen}(\alpha) = y$ y $\cos(\alpha) = x$, así:

También podemos definir la tangente del ángulo como su seno dividido por su coseno:

Lo que, por supuesto, nos dará el mismo resultado.

Otro método es utilizar nuestra calculadora del círculo unitario, por supuesto. 😁

Pero, ¿y si no estás satisfecho sólo con este valor, y te gustaría realmente ver ese valor de tangente en tu círculo unitario?

Es un poco más complicado que determinar el seno y el coseno, que son simplemente las coordenadas. Hay dos formas de mostrar la tangente del círculo unitario:

Método 1:

1. Crea una recta tangente en el punto $A$.
2. Intersecará al eje x en el punto $B$.
3. La longitud del segmento $\bar{AB}$ es el valor de la tangente

Método 2:

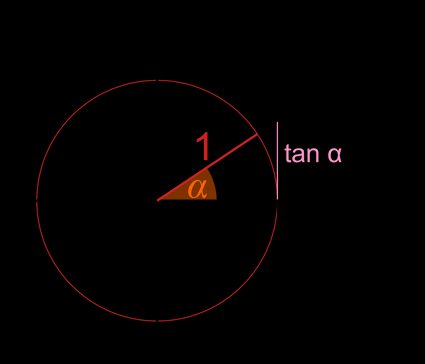
1. Traza una recta $x = 1$.
2. Prolonga la recta que contiene el radio.
3. Nombra la intersección de estas dos rectas como punto $C$.
4. La tangente, $\tan(\alpha)$, es la coordenada y del punto $C$.

En ambos métodos, hemos creado triángulos rectángulos con su lado adyacente igual a 1 😎

El seno, el coseno y la tangente no son las únicas funciones que puedes construir sobre el círculo unitario. Además de la cofunción tangente (cotangente), puedes presentar otras funciones menos conocidas, por ejemplo, la secante, la cosecante y el arcaico verseno:

El concepto de círculo unitario es muy importante porque puedes utilizarlo para hallar el seno y el coseno de cualquier ángulo. A continuación te presentamos algunos ángulos frecuentes en el diagrama del círculo unitario:

Por ejemplo, ¿cómo determinar $\text{sen}(150\degree)$?

1. Busca el ángulo $150\degree$.
2. Como hemos aprendido antes, el seno es una coordenada y, por tanto, tomamos la segunda coordenada del punto correspondiente del círculo unitario:

Alternativamente, introduce el ángulo 150° en nuestra calculadora del círculo unitario. Te mostraremos el valor $\text{sen}(150\degree)$ de tu coordenada y, así como el coseno, la tangente y el gráfico del círculo unitario.

Bueno, depende de lo que quieras memorizar 🙃 Hay dos cosas que debes recordar cuando se trata del círculo unitario:

1. Conversión de ángulos, es decir, cómo cambiar entre un ángulo en grados y uno en términos de $\pi$ (radianes del círculo unitario);

2. Las funciones trigonométricas de los ángulos populares.

Empecemos por la primera parte, más fácil. Los ángulos más importantes son los que utilizarás todo el tiempo:

• $30\degree = \pi/6$;
• $45\degree = \pi/4$;
• $60\degree = \pi/3$;
• $90\degree = \pi/2$;
• Ángulo completo, $360\degree = 2\pi$.

Como estos ángulos son muy comunes, intenta aprenderlos de memoria ❤️. Para cualquier otro ángulo, puedes utilizar la fórmula de conversión de ángulos:

¡La conversión de radianes del círculo unitario a grados ya no debería ser un problema! 💪

La otra parte (memorizar toda la gráfica del círculo unitario, con los valores del seno y el coseno) es un proceso algo más largo. No lo describiremos aquí, pero no dudes en consultar 3 consejos esenciales sobre cómo recordar el círculo unitario o esta página de WikiHow. Si prefieres ver vídeos 🖥️ a leer 📘, mira uno de estos dos vídeos que explican cómo memorizar el círculo unitario:

• Un truco para recordar valores en el círculo unitario;
• Cómo memorizar el círculo unitario en minutos

Además, esta tabla con ángulos de uso común puede resultarte útil:

Y si algún método falla, no dudes en utilizar nuestra calculadora del círculo unitario: está aquí para ti, para siempre ❤️ ¡Esperemos que jugar con la herramienta te ayude a comprender y memorizar los valores del círculo unitario!

tan 30° = 1/√3. Para hallar esta respuesta en el círculo unitario, empezamos hallando los valores del sen y del cos como coordenada y y coordenada x, respectivamente: sen 30° = 1/2 y cos 30° = √3/2. Ahora utiliza la fórmula. Recuerda que tan 30° = sen 30° / cos 30° = (1/2) / (√3/2) = 1/√3, como se ha dicho. ¿Ves qué fácil es?

Determinar la cosecante de θ en el círculo unitario:

1. Desde el centro del círculo traza el radio correspondiente al ángulo θ.
2. Traza rectas tangentes al círculo en los puntos (0,1) y (0,-1).
3. Prolonga el radio del Paso 1 de forma que intersecte a una de esas tangentes.
4. La distancia del centro al punto de intersección del Paso 3 es la cosecante de tu ángulo θ.
5. Si no hay punto de intersección, la cosecante de θ es indefinida (esto ocurre cuando sen θ = 0).

Como el arcoseno es la inversa de la función seno, encontrar arcsen(1/2) equivale a encontrar un ángulo cuyo seno sea igual a 1/2. En el círculo unitario, los valores del seno son las coordenadas y de los puntos del círculo. Observando el círculo unitario, vemos que la coordenada y es igual a 1/2 para el ángulo π/6, es decir, 30°.