Calculadora de arcotangente

Q: ¿A cuánto equivale arctg(x)?

El arctg(x) es igual a la función tangente inversa: tan-¹(x) . Si en un triángulo rectángulo, la tangente del ángulo determina el cociente entre la perpendicular y la base ( tg(x) = perpendicular / base ), entonces arctg nos ayudará a sacar el valor del ángulo x: x = tg-¹(perpendicular / base) .

Q: ¿Es arctglo mismo que tg-¹?

Sí , arctg es lo mismo que tg-¹ y significa la función tangente inversa. Sin embargo, ten cuidado de no confundir tg-¹(x) con (tg(x))-¹ , que significa 1/tg(x) y se refiere a otra función trigonométrica, la cotangente de x .

Q: ¿Qué es un arctg 1?

Arctg 1 (o tg inverso 1 ) da la medida del ángulo de un triángulo rectángulo en el que la razón del lado opuesto y el lado adyacente al ángulo es igual a 1 . El valor de arctg 1 es 45° o π/4 radianes .

Q: ¿Cuál es el arctg de la √3?

El valor exacto de arctg(√3) es 60° o π/3 . Como tg(60°) = √3 y arctg es la función tg inversa, arctg(√3) será 60°.

Q: ¿Cómo puedo dibujar la gráfica de arctg?

Para dibujar la gráfica de arctg y leer los valores de determinados ángulos: Dibuja un sistema de coordenadas , donde el eje y sea el eje horizontal y el eje x sea el eje vertical. Dibuja la gráfica de x = tg(y) pero sólo en el intervalo <-π/2;π/2> . Rota la gráfica 90 grados en el sentido de las agujas del reloj . ¡Ya lo tienes! Es una gráfica de y = arctg(x) .

Q: ¿Cuál es la integral del arctg?

Como arctg(x) = tg-¹(x) , la integral de arctg es la integración del inverso de tg x, que podemos escribir matemáticamente como: ∫tg-¹(x) dx = x tg-¹(x) - ½ ln |1+x²| + C En esta ecuación, C es la constante de integración, dx denota que la integración del inverso de tg x es con respecto a x, y ∫ denota el símbolo de integración.

Q: ¿Cuál es la derivada de arctg?

La derivada de la función arctg es: d/dx(arctg(x)) = 1/(1+x²) . La función arctg se puede diferenciar porque su derivada existe en todos los puntos de su dominio. Si observas la gráfica del período único de la función arctg(x), verás que la curva es continua .

Creadores

Hanna Pamuła, doctorado/a

Hanna Pamuła

PhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Traductores

Luis Hoyos

Luis is a mechanical engineer who works at Omni Calculator as a content creator and researcher specializing in math and physics calculators with a focus on thermodynamics and classical mechanics. With a strong foundation in mechanical engineering, Luis is passionate about creating tools that simplify complex concepts and improve everyday life. Outside of work, Luis likes weightlifting and applying his engineering knowledge to optimize the thermal conditions of his home, all while caring for four beloved cats. See full profile

Check our editorial policy

Supervisores

Bogna Szyk y Jack Bowater

¡Nuevo!

Utiliza esta calculadora de arctg para calcular rápidamente la tangente inversa. Tanto si quieres saber "¿qué es un arctan o arctg?" como si sientes curiosidad por la integral o la derivada del arctan, has llegado al lugar adecuado. A continuación, también encontrarás la gráfica de arcotangente, así como una tabla ordenada con valores de uso común, como arctg(1) y arctg(0). También puedes escribir el valor que te interese en esta herramienta y encontrarás la respuesta en un abrir y cerrar de ojos.

¿Te interesa la trigonometría más avanzada? Consulta nuestras calculadoras calculadora de la ley de los senos y calculadora de la ley de los cosenos 🇺🇸 si tienes algún triángulo que resolver.

Antes de calcular el arcotangente: ¿Qué es el arctg?

En arcotangente es la inversa de la función tangente. Para un análisis en profundidad de la tangente, visita nuestra calculadora de tangentes 🇺🇸. Puede abreviarse como arctan o arctg. En pocas palabras, utilizamos el arctg cuando queremos encontrar un ángulo para el que conocemos el valor de la tangente.

Sin embargo, en sentido estricto, como la tangente es una función trigonométrica periódica, no tiene función inversa. Aun así, podemos definir una función inversa si restringimos el dominio al intervalo en el que la función es monótona. El intervalo comúnmente elegido, $-\frac{\pi}{2}<y<\frac{\pi}{2}$ , se denomina valor principal y es, al mismo tiempo, el ámbito de una función tangente inversa.

Abreviación	Definición	Domino	Rango común de valores principales
$\text{arctg}(x)$
$\text{tg}^{-1}(x)$	$x = \tg(y)$	all real numbers $\mathbb{R}$	$-\frac{\pi}{2}<y<\frac{\pi}{2}$ $-90\degree<y<90\degree$
$\text{arctg}(x)$

Utilizar la convención $\tg^{-1}(x)$ puede llevar a confusión sobre la diferencia entre arcotangente y cotangente. Resulta que arctg y cot son en realidad cosas distintas:

$\cot(x) = 1/\tg(x)$ por lo que la cotangente es básicamente el recíproco de una tangente o, en otras palabras, el inverso multiplicativo.
$\arctg(x)$ es el ángulo cuya tangente es $x$ .

Esperamos que tengas ya claro que arctg y cotg son diferentes. Para evitar más malentendidos, quizá quieras **utilizar la notación $\arctg(x)$ en lugar de $\tg^{-1}(x)$ **.

🙋 ¡Explora Omni Calculator si quieres aprender a calcular todas las funciones trigonométricas 🇺🇸!

Entendiendo la calculadora del arctg: las gráficas arctg

Restringiendo el dominio de la función tangente principal, obtenemos la tangente inversa que oscila entre $-\frac{\pi}{2}<y<\frac{\pi}{2}$ radianes exclusivamente. Sin embargo, el dominio de una función arcotangente son todos los números reales. Entonces la gráfica tiene el siguiente aspecto:

$\boldsymbol{x}$	$\boldsymbol{\arctg(x)}$
	rad	grados
$-\infty$	$-\pi/2$	$-90\degree$
$-3$	$-1.2490$	$-71.565\degree$
$-2$	$-1.1071$	$-63.435\degree$
$-\sqrt 3$	$-\pi/3$	$-60\degree$
$-1$	$-\pi/4$	$-45\degree$
$-\sqrt{3}/3$	$-\pi/6$	$-30\degree$
$0$	$0$	$0$
$\sqrt{3}/3$	$\pi/6$	$30\degree$
$1$	$\pi/4$	$45\degree$
$\sqrt 3$	$\pi/3$	$60\degree$
$2$	$1.1071$	$63.435\degree$
$3$	$1.2490$	$71.565\degree$
$\infty$	$\pi/2$	$90\degree$

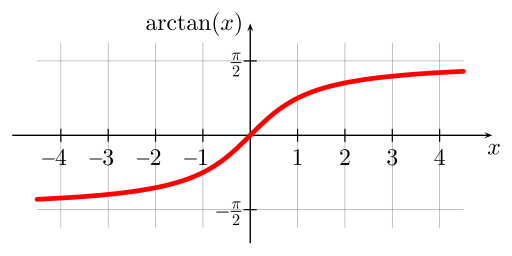
¿Cómo se crea este gráfico arcotangente? Reflejando el $\tg(x)$ en el intervalo $(-\pi/2, \pi/2)$ a través de la recta $y = x$ . También puedes verlo como una permutación de los ejes horizontal y vertical:

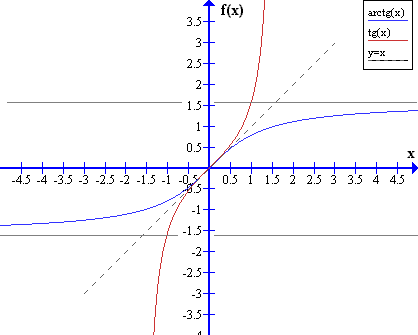
Propiedades del arctg, relaciones con las funciones trigonométricas, integral y derivadas del arctg

Las relaciones en trigonometría son cruciales para comprender este tema aún más a fondo. Inspeccionar el triángulo rectángulo con longitudes del lado $1$ y $x$ es un buen punto de partida si quieres encontrar las relaciones entre arctan o arctg y las funciones trigonométricas básicas:

Seno: $\sin(\arctg(x)) = x / \sqrt{1 + x^2}$ ;
Coseno: $\cos(\arctg(x)) = 1 / \sqrt{1 + x^2}$ ;
Tangente: $\tg(\arctg(x)) = x$ .

Otras relaciones útiles con el arcotangente son:

$\arctg(x) = \pi/2 -\text{arccot}(x)$ .
$\arctg(-x) = -\arctg(x)$ .
$\arcsin(x) = \arctg\left(x / \sqrt{1 - x^2}\right)$ (aprende sobre el arcsen en la calculadora de arcsin 🇺🇸).
Integral de arctg:

\begin{split} &\int\arctg(x) \text{d}x\\ & \!=\! x \arctg(x)\! -\! \frac{1}{2}\ln(1 \!+\! x^2) \!+ \!C \end{split}

Derivadas de arctg o arctan:

\frac{\text{d}}{\text{d}x}\! \arctg(x) \! =\! \frac{1}{1 \!+\! x^2}\ \text{if}\ x\! \neq\! \pm\text{i}

$\arctg(x) + \arctg(1/x) = \pi/2$ , for $x > 0$ and $\arctg(x) + \arctg(1/x) = -\pi/2$ , for $x < 0$

Es fácil demostrar la primera ecuación a partir de las propiedades del triángulo rectángulo con longitudes del lado $1$ y $x$ , ya que sabemos perfectamente que la suma de los ángulos de un triángulo es igual a $180\degree$ . Restando el ángulo recto, que es $90\degree$ , nos quedan dos ángulos no rectos, que deben sumar $90\degree$ . Así, podemos escribir los ángulos como $\arctg(x)$ y $\arctg(1/x)$ .

Cómo usar la calculador de arctg o arctan para sacar el arcotangente

Esta es una de nuestras calculadoras más fáciles de usar, ¡de verdad! Sólo tienes que introducir el número del que quieres sacar el arctg. Como el dominio del arctgson todos los números reales, no tienes que preocuparte de más. Digamos que queremos calcular el arctg de 1. Sólo tienes que introducir el número y la calculadora de la tangente inversa mostrará el resultado. Como esperábamos, el arctg de 1 es igual a $45\degree$ . Esta calculadora del arctg también funciona al revés, es decir, como una calculadora de tangentes estándar: escribe el ángulo en la segunda casilla y aparecerá la tangente de ese ángulo.

Preguntas frecuentes

¿A cuánto equivale arctg(x)?

El arctg(x) es igual a la función tangente inversa: tan-¹(x). Si en un triángulo rectángulo, la tangente del ángulo determina el cociente entre la perpendicular y la base (tg(x) = perpendicular / base), entonces arctg nos ayudará a sacar el valor del ángulo x: x = tg-¹(perpendicular / base).

¿Es arctglo mismo que tg-¹?

Sí, arctg es lo mismo que tg-¹ y significa la función tangente inversa. Sin embargo, ten cuidado de no confundir tg-¹(x) con (tg(x))-¹, que significa 1/tg(x) y se refiere a otra función trigonométrica, la cotangente de x.

¿Qué es un arctg 1?

Arctg 1 (o tg inverso 1) da la medida del ángulo de un triángulo rectángulo en el que la razón del lado opuesto y el lado adyacente al ángulo es igual a 1. El valor de arctg 1 es 45° o π/4 radianes.

¿Cuál es el arctg de la √3?

El valor exacto de arctg(√3) es 60° o π/3. Como tg(60°) = √3 y arctg es la función tg inversa, arctg(√3) será 60°.

¿Cómo puedo dibujar la gráfica de arctg?

Para dibujar la gráfica de arctg y leer los valores de determinados ángulos:

Dibuja un sistema de coordenadas, donde el eje y sea el eje horizontal y el eje x sea el eje vertical.
Dibuja la gráfica de x = tg(y) pero sólo en el intervalo <-π/2;π/2>.
Rota la gráfica 90 grados en el sentido de las agujas del reloj.
¡Ya lo tienes! Es una gráfica de y = arctg(x).

¿Cuál es la integral del arctg?

Como arctg(x) = tg-¹(x), la integral de arctg es la integración del inverso de tg x, que podemos escribir matemáticamente como:

∫tg-¹(x) dx = x tg-¹(x) - ½ ln |1+x²| + C

En esta ecuación, C es la constante de integración, dx denota que la integración del inverso de tg x es con respecto a x, y ∫ denota el símbolo de integración.

¿Cuál es la derivada de arctg?

La derivada de la función arctg es: d/dx(arctg(x)) = 1/(1+x²). La función arctg se puede diferenciar porque su derivada existe en todos los puntos de su dominio. Si observas la gráfica del período único de la función arctg(x), verás que la curva es continua.