Calculadora del ángulo entre dos vectores

Con esta calculadora de ángulos entre dos vectores, aprenderás rápidamente a encontrar el ángulo entre dos vectores. No importa si tus vectores están en 2D o 3D, ni si están representados por coordenadas o puntos inicial y final: nuestra herramienta te será útil en todos los casos. Juega un poco con la calculadora y consulta las definiciones y explicaciones que aparecen a continuación; si estás buscando las fórmulas del ángulo entre dos vectores, seguro que las encontrarás.

En esta sección encontrarás las fórmulas del ángulo entre dos vectores, y solo las fórmulas. Si quieres entender cómo las obtenemos, ve directamente a la siguiente sección, Cómo hallar el ángulo entre dos vectores.

Ángulo entre dos vectores 2D

1. Vectores representados por coordenadas (notación estándar de conjunto ordenado, en sus componentes):

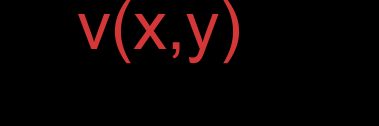
Para el vector $\boldsymbol a$:

Y $\boldsymbol b$:

El ángulo es:

2. Vectores entre un punto inicial y un punto final:

Para el vector $\boldsymbol a$:

Y:

Así que el vector $\boldsymbol a$ es:

Para el vector $\boldsymbol b$:

Y:

Así que el vector $\boldsymbol b$ es:

Y:

Ángulo entre dos vectores 3D

1. Vectores representados por coordenadas:

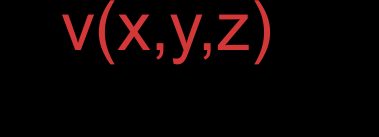
Y:

Entonces:

2. Vectores entre un punto inicial y un punto final:

Para el vector $\boldsymbol{a}$:

Y:

Así que:

Para el vector $\boldsymbol{b}$:

Y:

Entonces:

De forma análoga a la versión 2D, obtén la fórmula final:

También es posible tener un vector definido por coordenadas y el otro definido por un punto inicial y final, pero no dejemos que eso complique aún más esta sección. Lo único que importa es que nuestra calculadora de ángulos entre dos vectores tiene todas las combinaciones posibles a tu disposición.

Muy bien, en la sección anterior nos enfocamos exclusivamente en la representación de las fórmulas. Pero, ahora, para entender mejor las fórmulas del ángulo entre dos vectores, veamos de dónde vienen:

1. Empecemos con la fórmula geométrica básica para calcular el producto punto 🇺🇸:

   El producto punto se define como el producto de las magnitudes de los vectores multiplicado por el coseno del ángulo entre ellos (aquí denotado por $\alpha$):

2. Entonces, haz que el ángulo sea el sujeto de la ecuación:

   Divide por el producto de las magnitudes de los vectores:

Halla el coseno inverso de ambos lados:

3. Ahora, repasemos la definición de la magnitud de un vector:

   Como la magnitud es la raíz cuadrada de la suma de las componentes del vector a la segunda potencia, nos encontramos con que:

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ en el espacio 2D; y

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ en el espacio 3D.

¿Notaste que es la misma fórmula que se utiliza en la calculadora de distancia? ¿Y que tiene su origen directamente en la geometría? Aprende a hacer esto con la calculadora del teorema de Pitágoras

4. Utiliza la fórmula algebraica del producto punto (suma de los productos de las componentes de los vectores), y sustituye las magnitudes:

En el espacio 2D:

Si los vectores $\boldsymbol{a}$ y $\boldsymbol{b}$ son, respectivamente:

Y:

En el espacio 3D:

Si los vectores $\boldsymbol{a}$ y $\boldsymbol{b}$ son, respectivamente:

Y:

Luego:

¡Y eso es todo!

Además, si tus vectores tienen una forma diferente (conoces sus puntos inicial y final), tendrás que realizar algunos cálculos de antemano. El objetivo es reducirlos a la notación vectorial estándar.

Si tu vector está descrito por el punto inicial $A=(x_1, y_1)$ y el punto final $B=(x_2, y_2)$, entonces el vector$\boldsymbol{a}$ puede expresarse como:

¿Aún no tiene sentido? ¡No te preocupes! Hemos preparado algunos ejemplos para aclarar cualquier duda que puedas tener.

Supongamos que queremos hallar el ángulo entre dos vectores:

y $\boldsymbol{b}$ definido como el vector entre el punto $A = (1, 1, 2)$ y $B = (-4, -8, 6)$.

¿Qué tenemos que hacer?

1. Primero, calcula el vector $\boldsymbol{b}$, dados los puntos inicial y final:

2. A continuación, determina el producto punto de los vectores $\boldsymbol{a}$ y $\boldsymbol{b}$:

3. Ahora, halla la magnitud de los vectores:

Y:

4. Por último, emplea la ecuación del producto escalar transformado:

¡Y ahí lo tienes! Acabas de calcular el ángulo entre dos vectores en 3D.

Si quieres aprender más conceptos de geometría de coordenadas, te recomendamos que consultes la calculadora de razón de cambio promedio.

Entonces, ¿cómo funciona nuestra calculadora de ángulos entre dos vectores? Sigue estas instrucciones paso a paso:

1. Elige tu espacio vectorial. Consideremos el mismo ejemplo de la sección anterior. Nuestros vectores y puntos tienen tres coordenadas, así que seleccionamos la opción 3D.

2. Selecciona la representación del primer vector. El primer vector está en notación estándar, así que dejamos el valor por defecto: representación en coordenadas.

3. Ingresa el primer vector. Escribe $x = 3,$ $y = 6,$ y $z = 1$.

4. Elige la representación del segundo vector. Esta vez tenemos que cambiarla a representación con punto.

5. Ingresa los valores del segundo vector. Introduce $\boldsymbol A = (1,1,2)$ y $\boldsymbol B = (-4,-8,6)$ en los campos correspondientes.

6. La herramienta indicará el ángulo entre los dos vectores 3D en el momento en que completes el último campo. En nuestro caso, es $150.2\degree$, que es, por supuesto, el mismo resultado que obtuvimos de los cálculos manuales.

Un vector es una elemento de un espacio vectorial que posee magnitud, dirección y sentido. Es muy común su uso para representar cantidades físicas tales como la fuerza, velocidad y desplazamiento, entre otras.

El ángulo formado entre dos vectores se define utilizando el coseno inverso de los productos escalares de los dos vectores y el producto de sus magnitudes.

Para calcular el ángulo entre dos vectores en un espacio 2D:

1. Halla el producto punto de los vectores.
2. Divide el producto punto por la magnitud del primer vector.
3. Divide el resultado por la magnitud del segundo vector.

Matemáticamente, el ángulo α entre dos vectores [x_a,y_a] y [x_b, y_b] se puede escribir como:

α = arccos[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))]

Para calcular el ángulo entre dos vectores en un espacio 3D:

1. Halla el producto punto de los vectores.
2. Divide el producto punto por la magnitud del primer vector.
3. Divide el resultado por la magnitud del segundo vector.

Matemáticamente, el ángulo α entre dos vectores [x_a,y_a,z_a] y [x_b, y_b,z_b] se puede escribir como:

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²))]