Calculadora de valor p

¡Bienvenido a nuestra calculadora de valor p! Nunca más tendrás que preguntarte cómo hallar el valor p, ya que aquí podrás determinar el valor p unilateral y bilateral de los estadísticos de prueba, con todas las distribuciones más populares: normal, t de Student, chi-cuadrado y F de Snedecor.

Los valores p aparecen en todas partes en la ciencia, pero a mucha gente le intimida un poco el concepto. No te preocupes: en este artículo te explicamos no sólo qué es el valor p, sino también cómo interpretar correctamente los valores p. ¿Alguna vez has sentido curiosidad por saber cómo calcular el valor p a mano? ¡También te proporcionamos todas las fórmulas necesarias!

Formalmente, el valor p es la probabilidad de que el estadístico de prueba produzca valores al menos tan extremos como el valor que produjo para tu muestra. ¡Es crucial recordar que esta probabilidad se calcula bajo el supuesto de que la hipótesis nula H₀ es cierta!

De forma más intuitiva, el valor p responde a la pregunta:

Suponiendo que vivo en un mundo en el que se cumple la hipótesis nula, ¿qué probabilidad hay de que, para otra muestra, la prueba que estoy realizando genere un valor al menos tan extremo como el que he observado para la muestra que ya tengo?

Es la hipótesis alternativa la que determina lo que realmente significa "extremo", por lo que el valor p depende de la hipótesis alternativa que plantees: de cola izquierda, de cola derecha o de dos colas. En las fórmulas siguientes, S representa un estadístico de prueba, x el valor que produjo para una muestra dada, y Pr(suceso | H₀) es la probabilidad de un suceso, calculada bajo el supuesto de que H₀ es cierta:

1. Prueba de cola izquierda:

   valor p = Pr(S ≤ x | H₀)

2. Prueba de cola derecha:

   valor p = Pr(S ≥ x | H₀)

3. Prueba de dos colas:

   valor p = 2 × min{Pr(S ≤ x | H₀), Pr(S ≥ x | H₀)}

   (Por min{a,b}, denotamos el número más pequeño entre a y b)

   Si la distribución de la estadística de la prueba bajo H₀ es simétrica respecto a 0, entonces:
   valor p = 2 × Pr(S ≥ |x| | H₀)

   o, lo que es lo mismo:
   valor p = 2 × Pr(S ≤ -|x| | H₀)

Como una imagen vale más que mil palabras, vamos a ilustrar estas definiciones. En este caso, utilizaremos el hecho de que la probabilidad puede representarse claramente como el área bajo la curva de densidad de una distribución dada. Mostraremos dos conjuntos de imágenes: uno para una distribución simétrica y otro para una distribución sesgada (no simétrica).

• Caso simétrico: distribución normal:

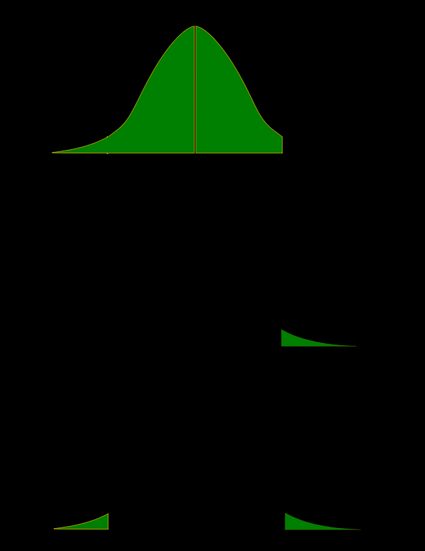
• Caso no simétrico: distribución chi-cuadrado:

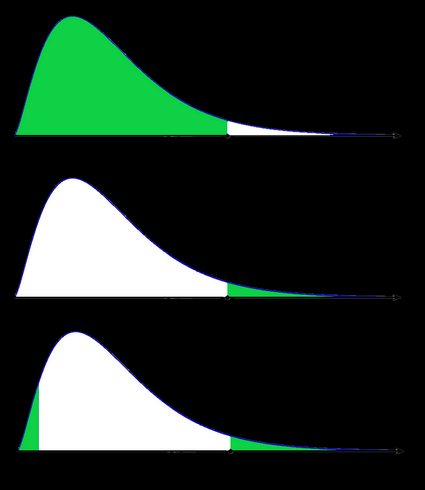
En la última imagen (valor p de dos colas para una distribución sesgada), el área del lado izquierdo es igual al área del lado derecho.

Para determinar el valor p, necesitas conocer la distribución de tu estadístico de prueba bajo el supuesto de que la hipótesis nula sea cierta. Luego, con la ayuda de la función de distribución acumulativa (FDA) de esta distribución, podemos expresar la probabilidad de que el estadístico de prueba sea al menos tan extremo como su valor x para la muestra:

1. Prueba de cola izquierda:

   valor p = FDA(x)

2. Prueba de cola derecha:

   valor p = 1 - FDA(x)

3. Prueba de dos colas:

   valor p = 2 × min{FDA(x) , 1 - FDA(x)}

   Si la distribución del estadístico de prueba bajo H₀ es simétrica respecto a 0, entonces un valor p de dos colas puede simplificarse a valor p = 2 × cdf(-|x|), o, equivalentemente, como valor p = 2 - 2 × cdf(|x|).

Las distribuciones de probabilidad más usuales en la verificación de hipótesis suelen tener fórmulas FDA complicadas, y encontrar el valor p a mano puede no ser posible. Es probable que tengas que recurrir a una computadora o a una tabla estadística, donde la gente ha reunido valores aproximados de la FDA.

Bien, ahora ya sabes cómo calcular el valor p, pero... ¿para qué necesitas calcular este número en primer lugar? Al contrastar una hipótesis, el método del valor p es una alternativa al método del valor crítico. Recordemos que este último requiere que los investigadores fijen previamente el nivel de significación, α, que es la probabilidad de rechazar la hipótesis nula cuando es cierta (es decir, de errores de tipo I). Una vez que tengas tu valor p, solo tienes que compararlo con cualquier α dado para decidir rápidamente si rechazas o no la hipótesis nula a ese nivel de significación, α. Para más detalles, consulta la siguiente sección, donde explicamos cómo interpretar los valores p.

Como hemos dicho antes, el valor p es la respuesta a la siguiente pregunta:

Suponiendo que vivo en un mundo en el que se cumple la hipótesis nula, ¿qué probabilidad hay de que, para otra muestra, la prueba que estoy realizando genere un valor al menos tan extremo como el que he observado para la muestra que ya tengo?

¿Qué significa esto para ti? Pues que tienes dos opciones:

• Un valor p alto significa que tus datos son muy compatibles con la hipótesis nula; y
• Un valor p pequeño aporta pruebas contra la hipótesis nula, ya que significa que tu resultado sería muy improbable si la hipótesis nula fuera cierta.

Sin embargo, ¡puede ocurrir que la hipótesis nula sea cierta, pero tu muestra sea muy inusual! Por ejemplo, imagina que estudiamos el efecto de un nuevo fármaco y obtenemos un valor p de 0.03. Esto significa que en el 3 % de los estudios similares, el azar por sí solo sería capaz de producir el valor del estadístico de prueba que obtuvimos, o un valor aún más extremo, ¡incluso si el fármaco no tuviera ningún efecto!

La pregunta "¿qué es el valor p?", también puede responderse como sigue: el valor p es el nivel de significación más pequeño en el que se rechazaría la hipótesis nula. Así pues, si ahora quieres tomar una decisión sobre la hipótesis nula a un cierto nivel de significación α, basta con comparar tu valor p con α:

• Si el valor p ≤ α, entonces rechazas la hipótesis nula y aceptas la hipótesis alternativa; y
• Si valor p ≥ α, entonces no tienes pruebas suficientes para rechazar la hipótesis nula.

Obviamente, el destino de la hipótesis nula depende de α. Por ejemplo, si el valor p fuera 0.03, rechazaríamos la hipótesis nula a un nivel de significación de 0.05, pero no a un nivel de 0.01. ¡Por eso el nivel de significación debe establecerse de antemano y no adaptarse convenientemente después de haber establecido el valor p! Un nivel de significación de 0.05 es el valor más común, pero no tiene nada de mágico. Aquí puedes ver como tener una fe demasiado fuerte en el umbral de 0.05 puede perjudicar un análisis. Siempre es mejor informar el valor p y dejar que el lector saque sus propias conclusiones.

Además, ten en cuenta que la experiencia en la materia (y el sentido común) son cruciales. De lo contrario, aplicar sin cuidado los principios estadísticos, pueden llevar fácilmente a algo estadísticamente significativo, a pesar de que la conclusión sea 100 % falsa.

Como nuestra calculadora de valor p está a tu servicio, ¡ya no tienes que preguntarte cómo hallar el valor p de todas esos complicados estadísticos de prueba! Aquí tienes los pasos que debes seguir:

1. Elige la hipótesis alternativa: de dos colas, de cola derecha o de cola izquierda.

2. Dinos la distribución de tu estadístico de prueba bajo la hipótesis nula: ¿es N(0,1), t de Student, chi-cuadrado o F de Snedecor? Si no estás seguro, consulta los apartados siguientes, ya que están dedicados a estas distribuciones.

3. De ser necesario, especifica los grados de libertad de la distribución del estadístico de prueba.

4. Introduce el valor del estadístico de prueba para tu muestra de datos.

5. Nuestra calculadora determina el valor p del estadístico de prueba y proporciona la decisión a tomar sobre la hipótesis nula. El nivel de significación estándar es 0.05 por defecto.

Ve al modo avanzado(advanced-mode) si necesitas aumentar la precisión con la que se realizan los cálculos o cambiar el nivel de significación.

En términos de la función de distribución acumulativa (FDA) de la distribución normal estándar, que tradicionalmente se denota por Φ, el valor p viene dado por las fórmulas siguientes:

1. Prueba z de cola izquierda:

   valor p = Φ(Z)

2. Prueba z de cola derecha:

   Valor p = 1 - Φ(Z)

3. Prueba z de dos colas:

   valor p = 2 × Φ(-|Z|)

   o

   valor-p = 2 - 2 × Φ(|Z|)

Utilizamos la puntuación Z si el estadístico de prueba sigue aproximadamente la distribución normal estándar N(0,1). Gracias al teorema del límite central, puedes tomar la aproximación si tienes una muestra grande (digamos al menos 50 puntos de datos) y tratar la distribución como normal.

Una prueba Z suele referirse a comparar la media poblacional, o la diferencia entre dos medias poblacionales, en particular entre dos proporciones. También puedes encontrar pruebas Z en las estimaciones de máxima verosimilitud.

El valor p de la puntuación t viene dado por las fórmulas siguientes, en las que FDA_t,d indica la función de distribución acumulativa de la distribución t de Student con d grados de libertad:

1. Prueba t de cola izquierda:

   valor p = FDA_t,d(t)

2. Prueba t de cola derecha:

   valor p = 1 - FDA_t,d(t)

3. Prueba t de dos colas:

   valor p = 2 × FDA_t,d(-|t|)

   o

   valor-p = 2 - 2 × FDA_t,d(|t|)

Utiliza la opción puntuación t si tu estadístico de prueba sigue la distribución t de Student. Esta distribución tiene una forma similar a N(0,1) (acampanada y simétrica) pero tiene colas más pesadas (la forma exacta depende del parámetro llamado grados de libertad). Si el número de grados de libertad es grande (mayor a 30), lo que ocurre en las muestras grandes, la distribución t de Student es prácticamente indistinguible de la distribución normal N(0,1).

Las pruebas t más habituales son las de medias poblacionales con una desviación estándar poblacional desconocida, o las de diferencia entre medias de dos poblaciones, con desviaciones estándar poblacionales iguales o desiguales pero desconocidas. También hay una prueba t para muestras emparejadas (dependientes).

Utiliza la opción χ² cuando realices una prueba en la que el estadístico de la prueba siga la distribución chi-cuadrado χ².

Esta distribución surge si, por ejemplo, tomas la suma de variables al cuadrado, cada una de las cuales sigue la distribución normal N(0,1). Recuerda comprobar el número de grados de libertad de la distribución χ² de tu estadístico de prueba.

¿Cómo hallar el valor p a partir de la prueba chi-cuadrado? Puedes hacerlo con ayuda de las fórmulas siguientes, en las que FDA_χ²,d denota la función de distribución acumulativa de la distribución χ² con d grados de libertad:

1. Prueba de χ² de cola izquierda:

   valor p = FDA_χ²,d(χ²)

2. Prueba de la χ² de cola derecha:

   valor p = 1 - FDA_χ²,d(χ²)

   Recuerda que las pruebas χ² de bondad de ajuste e independencia son pruebas de cola derecha (lee debajo para más información)

3. Prueba de χ² de dos colas:

   valor p = 2 × min{FDA_χ²,d(χ²), 1 - FDA_χ²,d(χ²)}

   (Por min{a,b}, denotamos el menor de los números a y b)

Los métodos más populares que dan lugar a una prueba χ² son los siguientes:

• Probar si la varianza de datos distribuidos normalmente tiene algún valor predeterminado. En este caso, el estadístico de prueba tiene la distribución χ² con n - 1 grados de libertad, donde n es el tamaño de la muestra. Puede ser una prueba de una cola o de dos colas.

• La prueba de bondad de ajuste comprueba si la distribución empírica (de la muestra) coincide con alguna distribución de probabilidad esperada. En este caso, el estadístico de prueba sigue la distribución χ² con k - 1 grados de libertad, donde k es el número de clases en que se divide la muestra. Se trata de una prueba de cola derecha.

• La prueba de independencia se utiliza para determinar si existe una relación estadísticamente significativa entre dos variables. En este caso, su estadístico de prueba se basa en la tabla de contingencia y sigue la distribución χ² con (r - 1)(c - 1) grados de libertad, donde r es el número de filas y c es el número de columnas de esta tabla de contingencia. También se trata de una prueba de cola derecha.

Por último, la opción prueba F debe utilizarse cuando realices una prueba en la que el estadístico de prueba siga la distribución F, también conocida como distribución Fisher-Snedecor. La forma exacta de una distribución F depende de dos grados de libertad.

Para ver de dónde proceden esos grados de libertad, considera las variables aleatorias independientes X e Y, que siguen ambas las distribuciones χ² con d₁ y d₂ grados de libertad, respectivamente. En ese caso, la relación (X/d₁)/(Y/d₂) sigue la distribución F, con (d₁, d₂) grados de libertad. Por este motivo, a los dos parámetros d₁ y d₂ también se les llaman grados de libertad del numerador y del denominador.

El valor p de prueba F viene dado por las fórmulas siguientes, en las que FDA_F,d1,d2 denota la función de distribución acumulativa de la distribución F, con (d₁, d₂)-grados de libertad:

1. Prueba F de cola izquierda:

   valor p = FDA_F,d1,d2(F)

2. Prueba F de cola derecha:

   valor p = 1 - FDA_F,d1,d2(F)

3. Prueba F de dos colas:

   valor p = 2 × min{FDA_F,d1,d2(F), 1 - FDA_F,d1,d2(F)}

   (Por min{a,b}, denotamos el menor de los números a y b)

A continuación enumeramos los métodos más importantes que producen pruebas F. Todas son pruebas de cola derecha.

• Una prueba para la igualdad de varianzas en dos poblaciones con distribución normal. Su estadístico de prueba sigue la distribución F con (n - 1, m - 1) grados de libertad, donde n y m son los tamaños de muestra respectivos.

• El ANOVA (análisis de la varianza) se utiliza para comparar la igualdad de medias en tres o más grupos que proceden de poblaciones distribuidas normalmente con varianzas iguales. Llegamos a una distribución F con (k - 1, n - k)-grados de libertad, donde k es el número de grupos, y n es el tamaño total de la muestra (en todos los grupos).

• Prueba de significación global de un análisis de regresión. El estadístico de prueba tiene una distribución F con (k - 1, n - k) grados de libertad, donde n es el tamaño de la muestra y k es el número de variables (incluida la intersección).

  Una vez establecida la relación lineal en tu muestra de datos con la prueba anterior, puedes calcular el coeficiente de determinación, R², que indica la fuerza de esta relación. Puedes hacerlo a mano o utilizar nuestra calculadora del coeficiente de determinación 🇺🇸.

• Prueba para comparar modelos anidados. El estadístico de prueba sigue la distribución F con (k₂ - k₁, n - k₂)-grados de libertad, donde k₁ y k₂ son los números de variables en el modelo menor y mayor, respectivamente, y n es el tamaño de la muestra.

  Puedes observar que la prueba F de significación global es una forma particular de la prueba F para comparar dos modelos anidados: comprueba si nuestro modelo obtiene resultados significativamente mejores que el modelo sin variables predictoras (es decir, el modelo de solo intersección).

No, el valor p no puede ser negativo. Esto se debe a que las probabilidades no pueden ser negativas, y el valor p es la probabilidad de que el estadístico de prueba cumpla determinadas condiciones.

Un valor p alto significa que, bajo la hipótesis nula, hay una alta probabilidad de que, para otra muestra, el estadístico de prueba genere un valor al menos tan extremo como el observado en la muestra que ya tienes. Un valor p alto no te permite rechazar la hipótesis nula.

Un valor p bajo significa que, bajo la hipótesis nula, hay poca probabilidad de que, para otra muestra, el estadístico de prueba genere un valor al menos tan extremo como el observado para la muestra que ya tienes. Un valor p bajo es una prueba a favor de la hipótesis alternativa: te permite rechazar la hipótesis nula.