Calculadora del intervalo de confianza
Esta calculadora del intervalo de confianza es una herramienta que te ayudará a encontrar el intervalo de confianza de una muestra, siempre que proporciones la media 🇺🇸, la desviación estándar y el tamaño de la muestra. Puedes utilizarla con cualquier nivel de confianza arbitrario. Si quieres saber qué es exactamente el intervalo de confianza y cómo calcularlo, o buscas la fórmula del intervalo para un 95 % de confianza para la puntuación z, este artículo seguro que te ayuda.
¿Qué es el intervalo de confianza?
La definición dice que “un intervalo de confianza es el rango de valores, derivado de la estadística muestral, que probablemente contenga al valor de un parámetro poblacional desconocido” Pero, ¿qué significa eso en la realidad?
Imagina que a un fabricante de ladrillos le preocupa si la masa de los ladrillos que fabrica se ajusta a las especificaciones. Ha medido que la masa media de una muestra de 100 ladrillos es igual a 3 kg. También ha determinado que el intervalo de confianza del 95 % está entre 2.85 kg y 3.15 kg. Esto significa que puede estar seguro al 95 % de que la masa media de los ladrillos que fabrica estará comprendida entre 2.85 kg y 3.15 kg. Más concretamente: si el fabricante de ladrillos tomara muchas muestras de 100 ladrillos cada una, y utilizara cada muestra para calcular el intervalo de confianza, entonces el 95 % de estos intervalos contendrán la verdadera masa media de un ladrillo.
Por supuesto, no siempre necesitas estar seguro al 95 %. Quizá quieras estar seguro al 99 %, o quizá te baste con que el intervalo de confianza sea correcto en el 90 % de los casos. Este porcentaje se denomina nivel de confianza.
Fórmula del intervalo de confianza de 95 %
Calcular el intervalo de confianza requiere que conozcas tres parámetros de tu muestra: el valor de la media, μ, la desviación estándar, σ, y el tamaño de la muestra, n (número de medidas tomadas). A continuación, puedes calcular el error estándar 🇺🇸 y luego el margen de error según las fórmulas siguientes:
error estándar = σ/√n
margen de error = error estándar × Z(0.95)
donde Z(0.95) es la puntuación z correspondiente al nivel de confianza del 95 %. Si utilizas un nivel de confianza diferente, deberás calcular la puntuación z correspondiente en lugar de este valor. Pero no te preocupes, ¡nuestra calculadora de puntaje z te facilitará esta tarea!
¿Cómo hallar el valor Z(0.95)? Es el valor de la puntuación z cuando el nivel de confianza de dos colas es igual al 95 %. Significa que si dibujas una curva de distribución normal 🇺🇸, el área entre las dos puntuaciones z será igual a 0.95 (de un total de 1).
Si quieres calcular este valor empleando una tabla de puntuaciones z, esto es lo que tienes que hacer:
- Decide tu nivel de confianza. Supongamos que es del 95 %.
- Calcula cuál es la probabilidad de que tu resultado no esté en el intervalo de confianza. Este valor es igual a 100 % – 95 % = 5 %.
- Observa la curva de distribución normal. El 95 % corresponde al área del centro. Eso significa que el área a la izquierda del opuesto de tu puntuación z es igual a 0.025 (2.5 %) y el área a la derecha de tu puntuación z también es igual a 0.025 (2.5 %).
- El área a la derecha de tu puntuación z es exactamente igual al valor p de tu puntuación z. Puedes utilizar tablas de puntuación z para encontrar la puntuación z que corresponde a un valor p de 0.025. En este caso, es 1.959.
Una vez calculado el valor Z(0.95), solo tienes que introducir este valor en la ecuación anterior para obtener el margen de error. Ahora solo queda hallar el límite inferior y superior del intervalo de confianza:
límite inferior = media - margen de error
límite superior = media + margen de error
¿Cómo calculo el intervalo de confianza?
Para calcular un intervalo de confianza (bilateral), tienes que seguir estos pasos:
- Supongamos que el tamaño de la muestra es
100. - Halla la media de tu muestra. Supongamos que es
3. - Determina la desviación estándar de la muestra. Supongamos que es
0.5. - Elige el nivel de confianza. El nivel de confianza más habitual es el
95 %. - Busca en la tabla estadística la puntuación Z(0.95), es decir, el cuantil 97.5 de N(0,1), que en nuestro caso es
1.959. - Calcula el error estándar como
σ/√n = 0.5/√100 = 0.05. - Multiplica este valor por la puntuación z para obtener el margen de error:
0.05 × 1.959 = 0.098. - Suma y resta el margen de error al valor de la media para obtener el intervalo de confianza. En nuestro caso, el intervalo de confianza está entre 2.902 y 3.098.
¡Y listo! Han sido muchos cálculos, ¿verdad? Por suerte, nuestra calculadora del nivel de confianza puede realizar todos estos cálculos por sí sola.
Aplicación del intervalo de confianza en el análisis de series temporales
Una forma peculiar de utilizar el intervalo de confianza es el análisis de series temporales, en el que el conjunto de datos de la muestra representa una secuencia de observaciones en un marco temporal concreto.
Un tema frecuente en estudios de este tipo es si un cambio en una variable afecta a otra variable en cuestión.
Para ser más concretos, consideremos la siguiente pregunta general que suele atraer el interés de los economistas: "¿Cómo afecta una variación de la tasa de interés al nivel de precios?"
Hay varias formas de enfocar esta cuestión, que implica un complejo análisis teórico y empírico, que está mucho más allá del alcance de este texto. Además, existen múltiples técnicas para estimar y aplicar intervalos de confianza, pero aun así, mediante este ejemplo, podemos representar la funcionalidad del intervalo de confianza en un problema más complicado.
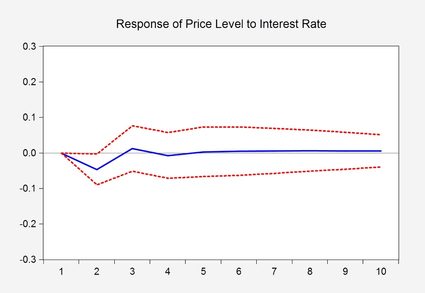
El gráfico anterior es una representación visual de un resultado de estimación de un modelo econométrico, la llamada función de impulso-respuesta, que muestra la reacción de una variable ante un cambio en la otra variable. Las líneas rojas discontinuas por debajo y por encima de la línea azul representan un intervalo de confianza del 95 %, también llamada banda de confianza, que define una región de resultados más probables. Más concretamente, muestra que tras un cambio en la tasa de interés, solo en el segundo mes se produce una respuesta significativa en el nivel de precios.
En resumen, esperamos que con los ejemplos anteriores y esta breve descripción, conozcas mejor la finalidad del intervalo de confianza, y ganes confianza para utilizar nuestra calculadora del intervalo de confianza.
FAQ
¿Cómo se interpretan los intervalos de confianza?
Si extraes muestras repetidamente y utilizas cada una de ellas para hallar un montón de intervalos de confianza del 95 % para una media poblacional, entonces la verdadera media poblacional estará contenida en aproximadamente el 95 % de estos intervalos de confianza. El 5 % restante no contendrá la verdadera media poblacional.
¿Cuál es la puntuación z de un intervalo de confianza del 95 %?
La puntuación z para un intervalo de confianza bilateral del 95 % es 1.959, que es el cuantil 97.5 de la distribución normal N(0,1).
¿Cuál es la puntuación z para un intervalo de confianza del 99 %?
La puntuación z para un intervalo de confianza bilateral del 99 % es 2.807, que es el cuantil 99.5 de la distribución normal N(0,1).
¿Cómo se aumenta la amplitud de un intervalo de confianza?
La amplitud de un intervalo de confianza aumenta cuando aumenta el margen de error, lo que ocurre cuando:
- aumenta el nivel de significación;
- disminuye el tamaño de la muestra; o
- aumenta la varianza de la muestra.
¿Cómo se achica la amplitud de un intervalo de confianza?
La amplitud de un intervalo de confianza disminuye cuando disminuye el margen de error, lo que ocurre cuando:
- disminuye el nivel de significación;
- aumenta el tamaño de la muestra; o
- disminuye la varianza de la muestra.
¡La media muestral no influye en la amplitud de un intervalo de confianza!
