Kritischer Wert Rechner

Willkommen beim Kritischer-Wert-Rechner! Hier kannst du schnell den/die kritischen Wert(e) für einseitige und zweiseitige Tests bestimmen. Du kannst hier den kritischen Wert für die meisten gängigen Verteilungen statistischer Tests berechnen: für die Gauß-/ Normalverteilung N(0,1) (für z-Wert), für die studentsche t-Verteilung, die Chi-Quadrat-Verteilung und die F-Verteilung (Fischer-Verteilung).

Was ist ein kritischer Wert? Und wie lautet die Formel für den kritischen Wert? Scrolle nach unten – wir erklären dir im folgenden Text die Definition des kritischen Werts und wie du kritische Werte berechnest, um den Ablehnungsbereich (auch kritischer Bereich genannt) zu definieren.

Mit dem Rechner für den kritischen Wert kannst du schnell die Grenzwerte von ein- und zweiseitigen statistischen Tests bestimmen. Um den Rechner effektiv zu nutzen, befolge diese Schritte:

1. Gib in das erste Feld die Verteilung deiner Test-Statistik unter der Nullhypothese ein: handelt es sich um eine Standard-Normalverteilung N (0,1), t-Student, Chi-Quadrat oder Snedecor's F? Wenn du dir nicht sicher bist, sieh dir die folgenden Abschnitte zu diesen Verteilungen an und versuche, den Test, den du durchführen musst, zu bestimmen.

2. Wähle im Feld Welche Art von Test? die Alternativhypothese aus: zweiseitig, rechts- oder links-seitig.

3. Gib bei Bedarf die Freiheitsgrade der Verteilung der Test-Statistik an. Wenn du mehr Informationen brauchst, schau in der Beschreibung des Tests nach, den du durchführst. Mehr über die Bedeutung dieser Größe in der Statistik erfährst du mit dem Freiheitsgrade Rechner.

4. Bestimme das Signifikanzniveau, $\alpha$. Standardmäßig ist es auf 0,05, festgelegt, aber du kannst es aber an deine Bedürfnisse anpassen.

5. Der Rechner für den kritischen Wert zeigt dir den/die kritischen Wert(e) und den/die Ablehnungsbereich(e) an.

6. Klicke auf den Erweiterten Modus, wenn du die Genauigkeit der Berechnung der kritischen Werte erhöhen möchtest.

**Nehmen wir zum Beispiel an, dass du einen einseitigen Hypothesentest mit einer studentschen t-Verteilung mit 15 Freiheitsgraden durchführst. Du hast dich für einen rechtsseitigen Test entschieden und ein Signifikanzniveau (α) von 0,05 festgelegt. Die Ergebnisse zeigen, dass der kritische Wert 1,7531 ist, und der kritische Bereich (1,7531, ∞) ist. Das bedeutet, dass du die Nullhypothese auf dem Signifikanzniveau von 0,05 ablehnst, wenn deine Test-Statistik den Wert 1,7531 übersteigt.

👩‍🏫 Möchtest du mehr über kritische Werte erfahren? Lies weiter!

Bei Hypothesentests sind die kritischen Werte einer der beiden Ansätze, mit denen du entscheiden kannst, ob du die Nullhypothese annehmen oder ablehnen solltest. Ein anderer Weg ist die Berechnung des p-Wertes (zum Beispiel mit dem p-Wert Rechner).

Bei der Berechnung des kritischen Werts wird geprüft, ob der Wert der Teststatistik aus deiner Stichprobe im Ablehnungsbereich/ kritischen Bereich liegt, d.h. in dem Bereich, in dem die Teststatistik mit hoher Wahrscheinlichkeit nicht liegt. Ein kritischer Wert ist ein Grenzwert (oder zwei Grenzwerte im Falle eines zweiseitigen Tests), der die Grenze der Ablehnungsbereiche bildet. Mit anderen Worten: Der kritische Wert teilt die Skala deiner Teststatistik in den Ablehnungs- und Annahmebereich auf.

Wenn du den Ablehnungsbereich bestimmt hast, prüfst du, ob der Wert der Teststatistik, der durch deine Stichprobe erzeugt wurde, innerhalb dieses Bereiches liegt:

• Wenn ja, bedeutet das, dass du die Nullhypothese H₀ ablehnen und die Alternativhypothese annehmen kannst.
• Wenn dein Wert stattdessen im Annahmebereich liegt, dann gibt es nicht genug Beweise, um H₀ zu verwerfen.

Aber wie werden kritische Werte berechnet? Zunächst musst du ein Signifikanzniveau $\alpha$ festlegen, das die Wahrscheinlichkeit angibt, dass die Nullhypothese verworfen wird, wenn sie tatsächlich richtig ist. Die Wahl von α ist willkürlich; in der Praxis verwenden wir meistens einen Wert von 0,05 oder 0,01. Die kritischen Werte hängen auch von der Alternativhypothese ab, die du für deinen Test wählst, was im nächsten Abschnitt erläutert wird.

Um kritische Werte zu bestimmen, musst du die Verteilung deiner Teststatistik kennen, unter der Annahme, dass die Nullhypothese gilt. Kritische Werte sind Punkte, die angeben, dass die Wahrscheinlichkeit, dass deine Teststatistik Werte annimmt, die mindestens so extrem sind wie diese kritischen Werte, gleich dem Signifikanzniveau α ist. Wow, was für eine Definition, nicht wahr? Keine Sorge, wir erläutern dir, was das alles bedeutet.

Zunächst möchten wir darauf hinweisen, dass es die Alternativhypothese ist, die bestimmt, was „extrem” bedeutet. Wenn der Test einseitig ist, gibt es nur einen kritischen Wert; wenn er zweiseitig ist, gibt es zwei: einen links und einen rechts vom Medianwert der Verteilung.

Kritische Werte lassen sich als Punkte darstellen, die die Eigenschaft haben, dass die Fläche unter der Dichtekurve der Teststatistik von diesen Punkten bis zu den Rändern gleich $\alpha$ ist:

• Linksseitiger Test (left-tailed): die Fläche unter der Dichtekurve vom kritischen Wert nach links ist gleich $\alpha$,

• Rechtsseitiger Test (right-tailed): die Fläche unter der Dichtekurve ab dem kritischen Wert nach rechts ist gleich $\alpha$, und

• Zweiseitiger Test (two-tailed): die Fläche unter der Dichtekurve vom linken kritischen Wert nach links ist gleich $\alpha/2$, und die Fläche unter der Kurve vom rechten kritischen Wert nach rechts ist ebenfalls gleich $\alpha/2$, die Gesamtfläche aus beiden ist also gleich $\alpha$.

Wie du siehst, läuft die Ermittlung der kritischen Werte für einen zweiseitigen Test mit dem Signifikanzniveau $\alpha$ darauf hinaus, die beiden einseitigen kritischen Werte mit einem Signifikanzniveau von $\alpha/2$ zu ermitteln.

Die Formeln für die kritischen Werte beziehen die Quantilsfunktion mit ein, $Q$, die die Umkehrung der kumulativen Verteilungsfunktion ($\mathrm{F}$) für die Verteilung der Teststatistik ist (berechnet unter der Annahme, dass H₀ gilt!): $Q = \mathrm{F}^{-1}$.

Sobald wir uns auf den Wert von $\alpha$ geeinigt haben, lauten die Formeln für den kritischen Wert wie folgt:

1. Linksseitiger Test:

2. Rechtsseitiger Test:

3. Zweiseitiger Test:

Im Falle einer Verteilung, die symmetrisch um 0 ist, sind die kritischen Werte für den zweiseitigen Test ebenfalls symmetrisch:

Leider haben die Wahrscheinlichkeitsverteilungen, die bei Hypothesentests am weitesten verbreitet sind, etwas komplizierte Formeln für die Verteilungsfunktion. Um die kritischen Werte handschriftlich zu ermitteln, müsstest du eine spezielle Software oder statistische Tabellen verwenden. In diesen Fällen ist die beste Option natürlich unser Kritischer-Wert-Rechner! 😁

Verwende die Option Z (Normalverteilung), wenn deine Teststatistik (zumindest ungefähr) der Standardnormalverteilung N(0,1) folgt.

In den folgenden Formeln bezeichnet $u$ die Quantilsfunktion der Standardnormalverteilung N(0,1):

1. Kritischer Z-Wert für den linksseitigen Test: $u(\alpha)$

2. Kritischer Z-Wert für den rechtsseitigen Test: $u(1-\alpha)$

3. Kritischer Z-Wert für den zweiseitigen Test: $\pm u(1- \alpha/2)$

Schau dir den Z-Test Rechner an, um mehr über den Z-Test für den Mittelwert der Grundgesamtheit zu erfahren. Es gibt auch Z-Tests für die Differenz zwischen zwei Mittelwerten, insbesondere zwischen zwei Proportionen.

Verwende die Option studentsche t-Verteilung, wenn deine Teststatistik der studentschen t-Verteilung folgt. Diese Verteilung ist ähnlich der Normalverteilung N(0,1), nur dass die Grenzen dicker sind – die genaue Form hängt von der Anzahl der Freiheitsgrade ab. Wenn diese Zahl groß ist (> 30), was in der Regel bei großen Stichprobenumfängen der Fall ist, dann ist die studentsche t-Verteilung praktisch nicht von N(0,1) zu unterscheiden. In unserem t-Statistik-Rechner kannst du die entsprechende Teststatistik berechnen.

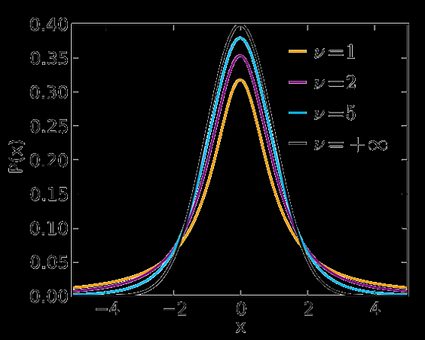
In den folgenden Formeln ist $Q_{\text{t}, f}$ die Quantilsfunktion der studentsche t-Verteilung mit $f$ Freiheitsgraden:

1. Kritischer t-Wert für den linksseitigen Test: $Q_{\text{t}, f}(\alpha)$

2. Kritischer t-Wert für den rechtsseitigen Test: $Q_{\text{t}, f}(1 - \alpha)$

3. Kritischer t-Wert für den zweiseitigen Test: $\pm Q_{\text{t}, f}(1 - \alpha/2)$

Schaue dir den t-Test-Rechner an, um mehr über verschiedene t-Tests, wie den für einen Mittelwert einer Population mit unbekannter Standardabweichung, den für die Differenz zwischen den Mittelwerten zweier Populationen (mit gleicher oder ungleicher Standardabweichung) oder den t-Test für gepaarte Stichproben zu erfahren.

Verwende die Option χ² (Chi-Quadrat), wenn du einen Test durchführst, bei dem die Teststatistik der χ²-Verteilung folgt.

Du musst dafür die Anzahl der Freiheitsgrade der χ²-Verteilung deiner Teststatistik bestimmen – im Folgenden listen wir sie für die am häufigsten verwendeten χ²-Tests auf.

Hier siehst du die Formeln für die kritischen Werte des Chi-Quadrats, wobei $Q_{\chi^2, d}$ die Quantilsfunktion der χ²-Verteilung mit $k$ Freiheitsgraden ist:

1. χ² kritischer Wert für den linksseitigen Test: $Q_{\chi^2, d}(\alpha)$

2. χ² kritischer Wert für den rechtsseitigen Test: $Q_{\chi^2, d}(1 - \alpha)$

3. χ² kritischer Wert für den zweiseitigen Test: $Q_{\chi^2, d}(\alpha/2)$ und $Q_{\chi^2, d}(1 - \alpha/2)$

Mehrere verschiedene Tests führen zu einem χ²-Wert:

• Test der Anpassungsgüte: Stimmt die empirische Verteilung mit der erwarteten Verteilung überein?

  Dieser Test ist rechtsseitig. Seine Teststatistik folgt der χ²-Verteilung mit $k - 1$ Freiheitsgraden, wobei $k$ die Anzahl der Klassen ist, in die die Stichprobe unterteilt wird.

• Unabhängigkeitstest: Gibt es eine statistisch signifikante Beziehung zwischen zwei Variablen?

  Dieser Test ist ebenfalls rechtsseitig und seine Teststatistik wird aus der Kontingenztafel berechnet. Es gibt $(r - 1)(c - 1)$ Freiheitsgrade, wobei $r$ die Anzahl der Zeilen und $c$ die Anzahl der Spalten der Kontingenztafel ist.

• Test auf die Varianz normalverteilter Daten: Hat diese Varianz einen bestimmten Wert?

  Dieser Test kann einseitig oder zweiseitig sein. Seine Teststatistik hat die χ²-Verteilung mit $n - 1$ Freiheitsgraden, wobei $n$ der Stichprobenumfang ist.

Wenn deine Teststatistik der F-Verteilung folgt, wähle diese. Diese Verteilung hat paarweise Freiheitsgrade.

Sehen wir uns an, wie diese Freiheitsgrade entstehen. Nehmen wir an, du hast zwei unabhängige Zufallsvariablen, $X$ und $Y$, die einer χ²-Verteilung mit $d_1$ bzw. $d_2$ Freiheitsgraden folgen. Wenn du nun das Verhältnis $(\frac{X}{d_1})/(\frac{Y}{d_2})$ betrachtest, stellt sich heraus, dass es der F-Verteilung mit $(d_1, d_2)$ Freiheitsgraden folgt. Deshalb nennen wir $d_1$ und $d_2$ die Freiheitsgrade des Zählers bzw. des Nenners.

In den folgenden Formeln steht $Q_{\text{F}, d_1, d_2}$ für die Quantilsfunktion der F-Verteilung mit $(d_1, d_2)$ Freiheitsgraden:

1. Kritischer F-Wert für den linksseitigen Test: $Q_{\text{F}, d_1, d_2}(\alpha)$

2. Kritischer F-Wert für den rechtsseitigen Test: $Q_{\text{F}, d_1, d_2}(1 - \alpha)$

3. Kritischer F-Wert für den zweiseitigen Test: $Q_{\text{F}, d_1, d_2}(\alpha/2)$ und $Q_{\text{F}, d_1, d_2}(1 -\alpha/2)$

Hier listen wir die wichtigsten Tests auf, die F-Scores erzeugen: Jeder von ihnen ist rechtsseitig.

• ANOVA: testet die Gleichheit der Mittelwerte in drei oder mehr Gruppen, die aus normalverteilten Grundgesamtheiten mit gleichen Varianzen stammen. Es gibt $(k - 1, n - k)$ Freiheitsgrade, wobei $k$ die Anzahl der Gruppen und $n$ der Gesamtstichprobenumfang (für jede Gruppe) ist.

• Gesamtsignifikanz der Regressionsanalyse. Die Teststatistik hat $(k - 1, n - k)$ Freiheitsgrade, wobei $n$ die Stichprobengröße und $k$ die Anzahl der Variablen (einschließlich des Achsenabschnitts) ist.

• Vergleich von zwei verschachtelten Regressionsmodellen. Die Teststatistik folgt der F-Verteilung mit $(k_2 - k_1, n - k_2)$ Freiheitsgraden, wobei $k_1$ und $k_2$ die Anzahl der Variablen im kleineren bzw. größeren Modell sind und $n$ der Stichprobenumfang ist.

• Die Gleichheit der Varianzen in zwei normalverteilten Populationen. Es gibt $(n - 1, m - 1)$ Freiheitsgrade, wobei $n$ und $m$ die jeweiligen Stichprobengrößen sind.

Das Mastermind hinter dem Rechner für den kritischen Wert ist Anna Szczepanek, eine promovierte Mathematikerin der Jagiellonen-Universität.

Die Idee zur Entwicklung des Tools entstand aus Annas Erfahrungen in Lehre und Forschung. Sie erkannte den Bedarf an einem Werkzeug, das die Bestimmung des kritischen Werts für verschiedene statistische Verteilungen vereinfacht, und entwickelte einen benutzerfreundlichen Rechner, der sowohl für Studierende als auch für Fachleute zugänglich ist. Nachdem sie das Tool veröffentlicht hatte, nutzte Anna den Rechner bald selbst in ihrer Forschung und als Lehr-Hilfsmittel.

Für Anna ist das Vertrauen in diesen Rechner von größter Bedeutung. Jedes Tool wird einem strengen Prüfungsprozess unterzogen, bei dem die Inhalte von Fachleuten geprüft und von Muttersprachlern sorgfältig Korrektur gelesen werden. Dieses Engagement für Genauigkeit und Zuverlässigkeit stellt sicher, dass die Nutzer/innen sich auf Omni's Inhalte verlassen können. Weitere Informationen zu unseren Standards findest in unseren Redaktionsrichtlinien.

Ein kritischer Z-Wert ist der Wert, der den kritischen Bereich bei Hypothesentests definiert, wenn die Teststatistik der Standardnormalverteilung folgt. Wenn der Wert der Teststatistik in den kritischen Bereich fällt, solltest du die Nullhypothese ablehnen und die Alternativhypothese annehmen.

Um einen kritischen Z-Wert für ein bestimmtes Konfidenzniveau α zu finden:

1. Prüfe, ob du einen ein- oder zweiseitigen Test durchführst.

2. Beim einseitigen Test:

   • Linksseitig: Der kritische Wert ist das **α-**Quantil der Standardnormalverteilung N(0,1).

   • Rechtsseitig: Der kritische Wert ist das (1-α) Quantil.

3. Zweiseitiger-Test: Der kritische Wert entspricht dem ±(1-α/2) Quantil von N(0,1).

4. Du hast keine Quantilstabellen parat? Verwende dafür einfach Standardnormalverteilungstabellen! (Die Quantilsfunktion ist der Kehrwert der Standardnormalverteilung.)

5. Überprüfe deine Antwort mit Omni's Rechner für kritische Werte.

In der Theorie, nein. In der Praxis, sehr oft, ja. Die studentsche t-Verteilung ist der Standard-Normalverteilung ähnlich, sie ist aber nicht dasselbe. Wenn jedoch die Anzahl der Freiheitsgrade (das ist grob gesagt dein Stichprobenumfang) groß genug ist (> 30), dann sind die beiden Verteilungen praktisch gleich und der kritische t-Wert hat den gleichen Wert wie der kritische Z-Wert.

Der kritische Z-Wert für ein 95%-Konfidenzintervall ist:

• 1,96 für einen zweiseitigen Test,
• 1,64 für einen rechtsseitigen Test und
• -1,64 für einen linksseitigen Test.