t-Test-Rechner

Willkommen bei unserem t-Test-Rechner!
Hier kannst du ganz einfach sowohl Einstichproben-t-Tests, als auch Zweistichproben-t-Tests und gepaarte t-Tests durchführen.
Wenn du den maximalen oder minimalen Grenzbereich, bei welchem die Nullhypothese noch abgelehnt werden kann, berechnen möchtest, schaue dir unseren p-Wert Rechner an. Falls du die kritischen Bereiche der t-Test Werte deiner Stichproben ermitteln möchtest, kannst du das auch mit diesem t-Test-Rechner hier tun! 😊

Was sagt ein t-Test eigentlich aus? Lies im folgenden Text, was mit verschiedenen Arten von t-Tests eigentlich getestet werden kann und wann t-Tests verwendet werden sollten (insbesondere, wann der Z-Test oder der t-Test verwendet wird). Wir erklären dir zudem, welche Bedingungen deine Stichproben oder Datensätze erfüllen sollten, um valide Ergebnisse zu produzieren. Wir zeigen dir auch, wie t-Tests handschriftlich durchgeführt werden können. Du findest hier alle notwendigen Formeln zum t-Test und erfährst, wie der Freiheitsgrad bestimmt wird.

Ein t-Test ist einer der gängigsten statistischen Hypothesentests zur Ermittlung der Streuung von Werten um den Mittelwert, d. h. er befasst sich mit dem/den Mittelwert(en) der Population(en).
Es gibt verschiedene Arten von t-Tests, die du durchführen kannst:

• der Einstichproben-t-Test,
• der Zweistichproben-t-Test und
• der gepaarte t-Test.

Im nächsten Abschnitt erklären wir dir, wann du welchen t-Test verwenden solltest.
Denke daran, dass ein t-Test nur für eine oder zwei Populationen verwendet werden kann. Wenn du drei (oder mehr) Mittelwerte vergleichen möchtest, führe eine Varianzanalyse durch (ANOVA, Englisch: Analysis of Variance).

Der t-Test zählt zu den parametrischen Tests, was bedeutet, dass deine Daten einige Annahmen erfüllen müssen:

• die Messwerte sind unabhängig UND
• die Werte folgen, zumindest annähernd, einer Normalverteilung.

Wenn du feststellst, dass deine Stichproben diese Annahmen nicht erfüllt, kannst du nicht-parametrische Hypothesentests wie in unserem Mann-Whitney-U-Test Rechner 🇺🇸 oder Wilcoxon-Rangsummentest Rechner 🇺🇸 verwenden. Eine weitere Möglichkeit ist der Wilcoxon-Vorzeichen-Rang-Test.

Die Wahl des t-Tests hängt davon ab, ob du eine oder zwei Populationen untersuchst:

• Einstichproben-t-Test (einfacher t-Test)

  Wähle diesen Test, um zu berechnen, ob der Mittelwert einer Population mit einer vordefinierten hypothetischen Größe übereinstimmt.

  Beispiele:

  • Das durchschnittliche Volumen eines Getränks, das in 0,33-Liter-Dosen verkauft wird — sind wirklich genau 330 ml in jeder Dose?
  • Das durchschnittliche Körpergewicht der Einwohner einer bestimmten Stadt — weicht es vom nationalen Durchschnitt ab?

• Zweistichproben-t-Test (doppelter t-Test)

  Wähle diesen Test, um zu prüfen, ob die Differenz zwischen den Mittelwerten zweier Populationen gleich einem vorgegebenen Sollwert ist, vorausgesetzt, die beiden Stichproben sind unabhängig voneinander.

  Mit diesem Test kannst du vor allem vergleichen, wie verschieden zwei Populationen voneinander sind.

  Beispiele:

  • Der durchschnittliche Unterschied in der Gewichtszunahme zweier Gruppen von Personen, wenn eine von denen beispielsweise eine kohlenhydratreiche Diät und die andere eine ketogene Diät durchführte.
  • Der durchschnittliche Unterschied in den Ergebnissen eines Mathe-Tests von Studenten an zwei verschiedenen Universitäten.

  Auf diese Tests wird sich auch mit den Synonymen unabhängiger t-Test oder ungepaarter t-Test bezogen.

• Gepaarter t-Test

  Ein gepaarter t-Test wird verwendet, um die Änderung des Mittelwerts einer Population zwischen zwei Zeitpunkten zu messen. Er basiert auf der Grundlage einer gepaarten Stichprobe, d. h. wenn beispielsweise das Gewicht jeder Person zweimal gemessen wurde — vor und nach der Diät.

  Mit diesem Test kannst du vor allem prüfen, ob eine Veränderung des zu untersuchenden Parameters im Durchschnitt eine Auswirkung auf die Population hatte.

  Beispiele:

  • Die Veränderung der Testleistungen von Schülern vor und nach der Teilnahme an einem Vorbereitungskurs.
  • Die Veränderung des Blutdrucks bei Patienten vor und nach der Behandlung mit einem neuen Medikament.

Du hast dich also entschieden, dass der t-Test der optimale Test für dein Problem ist.
In den folgenden Zeilen erfährst du, wie du den p-Wert des t-Tests und seine Grenzwerte berechnest und welche Schlussfolgerungen du dann bezüglich der Nullhypothese ziehen kannst.

Wie anfangs bereits erwähnt, ergibt jeder t-Test einen Mittelwertbereich sowie maximale und minimale Grenzwerte. Der p-Wert gibt an, bis zu welchem Grenzwert du die Nullhypothese, also die Annahme einer Aussage, noch ablehnen kannst. Je kleiner der p-Wert ist, desto signifikanter ist der Wert aus dem t-Test.
Die anfängliche Aussage (Nullhypothese), welche es gilt zu widerlegen, wird als H₀ ausgedrückt und die entsprechende Gegenhypothese als H₁.
Du kannst nun entscheiden, ob du wissen möchtest, wie groß die Spanne des Mittelwertes für beide Populationen ist (zweiseitiger t-Test) oder wie groß die Spanne des Mittelwertes für eine spezielle Population ist (einseitiger t-Test).

1. Entscheide dich für die passende Gegenhypothese:

   • Verwende einen zweiseitigen t-Test, wenn es dir ausschließlich darum geht, ob der Mittelwert der Population (oder, im Falle von zwei Populationen, die Differenz zwischen den Mittelwerten der Populationen) mit der Prüfgröße übereinstimmt bzw. nicht übereinstimmt.

   • Verwende einen einseitigen t-Test, wenn du prüfen möchtest, ob dieser Mittelwert (oder die Differenz der Mittelwerte) größer bzw. kleiner als die Prüfgröße ist.

2. Berechne deinen t-Test-Wert:

   Die Formeln für die Teststatistik bei t-Tests enthalten den Stichprobenumfang, deren Mittelwert und die Standardabweichung. Die genauen Formeln variieren je nach Art des t-Tests etwas — weitere Einzelheiten findest du in den entprechenden Abschnitten zu den Tests.

3. Bestimme die Anzahl der Freiheitsgrade für den t-Test:

   Die Freiheitsgrade sind die Anzahl der Beobachtungen in einer Stichprobe, die bei der Schätzung statistischer Parameter frei variieren können. Im einfachsten Fall ist: Freiheitsgrad = Stichprobenumfang - Anzahl der zu schätzenden Parameter. Auch hier hängt die genaue Formel von dem t-Test ab, den du durchführen möchtest — weitere Einzelheiten findest du in den entsprechenden Abschnitten zu den Tests.

Die Freiheitsgrade sind entscheidend, da sie die Verteilung bestimmen, welcher der t-Test Wert (unter Annahme der Nullhypothese) folgt. Wenn es f Freiheitsgrade gibt, dann ist die Verteilung der Teststatistik die Student-t-Verteilung mit f Freiheitsgraden. Diese Verteilung ähnelt der Normalverteilung N(0,1), glockenförmig und symmetrisch. Die tatsächliche Verteilungskurve ist aber flacher, die Ablehnungsbereiche sind also länger gezogen. Je größer die Anzahl der Freiheitsgrade (f > 30), was im Allgemeinen bei großen Stichprobenumfängen der Fall ist, desto mehr nähert sich die Kurve der Student-t-Test-Verteilung der einer Normalverteilung an.

Der p-Wert ist die (unter der Annahme, dass die Nullhypothese wahr ist berechnete) Wahrscheinlichkeit, dass die Teststatistik Werte ergibt, die mindestens so extrem sind wie der für deine Stichproben erzeugte t-Test-Wert. Da die Wahrscheinlichkeiten den Flächen unter der Dichtefunktion entsprechen, lässt sich der p-Wert des t-Tests mithilfe der folgenden Abbildungen sehr verständlich veranschaulichen:

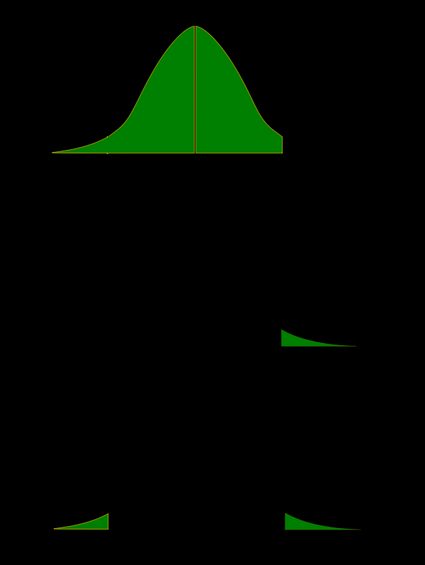
Mit den nun folgenden Formeln wird der p-Wert eines t-Tests berechnet. Mit CDF_t,f bezeichnen wir die kumulative Verteilungsfunktion (Englisch: cumultative distribution function) der Student-t-Test-Verteilung mit f Freiheitsgraden:

1. p-Wert aus linksseitigem t-Test (maximaler Grenzwert):

   p-Wert = CDF_t,f(t-Test_Wert)

2. p-Wert aus rechtsseitigem t-Test (minimaler Grenzwert):

   p-Wert = 1 - CDF_t,f(t-Test_Wert)

3. p-Wert aus zweiseitigem t-Test:

   p-Wert = 2 ∙ CDF_t,f(-|t-Test_Wert|)

   oder, äquivalent dazu: p-Wert = 2 - 2 ∙ CDF_t,f(|t-Test_Wert|)

Der CDF-Wert der t-Test-Verteilung wird durch eine etwas komplizierte Formel angegeben. Um den p-Wert handschriftlich zu ermitteln, musst du auf statistische Tabellen zurückgreifen, in denen ungefähre CDF-Werte aufgelistet sind, oder ein spezielles Statistikprogramm verwenden. Zum Glück nimmt dir unser t-Test-Rechner diesen Aufwand ab und ermittelt den p-Wert des t-Tests für dich im Handumdrehen!

Bevor die kritischen Werte berechnet werden können, aus welchen die Ablehnungsbereiche gebildet werden, muss ein Signifikanzniveau α festgelegt werden. Dieses gibt die Wahrscheinlichkeit an, die Nullhypothese ablehnen zu können, unter der Annahme, dass diese wahr ist.

Die Formeln für die kritischen Werte verwenden die Quantilfunktion der Student-t-Test-Verteilung, d. h. die Inverse der CDF/ Verteilungsfunktion:

1. kritischer Wert für linksseitigen t-Test:
   CDF_t,f^-1(α)

   Ablehnungsbereich:

   (-∞, CDF_t,f^-1(α)]

2. kritischer Wert für rechtsseitigen t-Test:
   CDF_t,f^-1(1-α)

   Ablehnungsbereich:

   [CDF_t,f^-1(1-α), ∞)

3. kritischer Wert für zweiseitigen t-Test:
   ±CDF_t,f^-1(1-α/2)

   Ablehnungsbereich:

   (-∞, -CDF_t,f^-1(1-α/2)] ∪ [CDF_t,f^-1(1-α/2), ∞)

Um zu entscheiden, ob die Nullhypothese bestätigt werden kann, prüfe einfach, ob dein t-Wert innerhalb des Ablehnungsbereiches liegt:

• Wenn der t-Wert im Ablehnungsbereich liegt, lehne die Nullhypothese ab und nimm die Gegenhypothese an.

• Liegt der t-Wert außerhalb des Ablehnungsbereiches, dann hast du nicht genügend Beweise, um die Nullhypothese ablehnen zu können.

1. Wähle den Typ des t-Tests, den du durchführen möchtest:

   • den Einstichproben-t-Test (um den Mittelwert einer einzelnen Population mit einer Prüfgröße zu vergleichen),
   • den Zweistichproben-t-Test (zum Vergleich der Mittelwerte zweier Populationen) oder
   • den gepaarten t-Test (um zu prüfen, wie sich der Mittelwert derselben Population nach einem bestimmten Eingriff verändert).

2. Entscheide dich für die Gegenhypothese:

   • zweiseitig ( μ ≠ μ₀),
   • linksseitig ( μ < μ₀ )oder
   • rechtsseitig ( μ > μ₀).

3. In unserem t-Test-Rechner kannst du entweder den p-Wert oder die Gkritischen We für deinen Hypothesentest verwenden!

4. Gib deinen t-Test Wert und die Anzahl der Freiheitsgrade f in die entsprechenden Felder des Rechners ein. Wenn du einen dieser Werte nicht kennst, gib stattdessen die Stichprobengröße, den Mittelwert und die Standardabweichung deiner Stichprobe(n) ein und unser t-Test-Rechner berechnet den t-Test Wert und die Freiheitsgrade automatisch für dich.

5. Sobald alle Parameter eingegeben sind, wird der p-Wert oder die Grenzwerte zusammen mit einer Interpretation sofort unter dem t-Test-Rechner angezeigt!

1. Die Nullhypothese H₀ besagt, dass der Mittelwert der Population gleich einem Wert $\mu_0$ ist (H₀ = μ₀) .

2. Die Gegenhypothese H₁ besagt, dass der Mittelwert der Population:

   • verschieden von $\mu_0$ ist ( μ ≠ μ₀),
   • kleiner als $\mu_0$ ist ( μ < μ₀) oder
   • größer als $\mu_0$ ( μ > μ₀) ist.

Formel für den Einstichproben t-Test:

wobei:

• $\mu_0$ — der in der Nullhypothese definierte Mittelwert,
• $n$ — der Stichprobenumfang,
• $\bar{x}$ — der Mittelwert der Stichprobe und
• $s$ —die Standardabweichung der Stichprobe.

Die Freiheitsgrade im Einstichproben-t-Test = $n-1$.

1. Die Nullhypothese H₀ ist, dass der tatsächliche Unterschied zwischen den Mittelwerten der Gruppen, $\mu_1$ und $\mu_2$, gleich dem gewählten Wert $\Delta$ ist.

2. Die Gegenhypothese H₁ stellt die zu untersuchende neue Hypothese auf, dass die Differenz $\mu_1 - \mu_2$ entweder:

   • verschieden von $\Delta$ ist,
   • kleiner als $\Delta$ ist oder
   • größer als $\Delta$ ist.

Wenn die Prüfgröße aus der Nullhypothese gleich Null ist ($\Delta = 0$) bedeutet das:

1. Die Nullhypothese behauptet, dass die Mittelwerte der Populationen gleich sind.

2. Die Gegenhypothese behauptet dann also über die Populationsmittelwerte:

   • $\mu_1$ und $\mu_2$ sind voneinander verschieden,
   • $\mu_1$ ist kleiner als $\mu_2$ oder
   • $\mu_1$ ist größer als $\mu_2$.

Um einen t-Test durchzuführen, wird zusätzlich angenommen, dass die Varianzen der beiden Populationen gleich sind – diese Annahme ist als die Homogenität der Varianz bekannt.

Es gibt eine Version des t-Tests, die ohne die Annahme der Homogenität der Varianz angewandt werden kann: den Welch-t-Test. Wir werden hier beide Optionen beschrieben.

Zweistichproben-t-Test für gleiche Varianzen:

Verwende diesen Test, wenn du weißt, dass die Varianzen der beiden Populationen gleich (oder sehr ähnlich) sind.

Formel für den Zweistichproben-t-Test bei gleichen Varianzen:

wobei $s_p$ die gepoolte Standardabweichung ist, welche wir folgendermaßen berechnen:

und

• $\Delta$ — der in der Nullhypothese angenommene Wert für die Differenz der Mittelwerte,
• $n_1$ — der Stichprobenumfang des ersten Datensatzes,
• $\bar{x}_1$ — der Mittelwert des ersten Datensatzes,
• $s_1$ — die Standardabweichung des ersten Datensatzes,
• $n_2$ — der Stichprobenumfang des zweiten Datensatzes,
• $\bar{x}_2$ — der Mittelwert des zweiten Datensatzes und
• $s_2$ — die Standardabweichung des zweiten Datensatzes.

Anzahl der Freiheitsgrade für Zweistichproben-t-Test für gleiche Varianzen = $n_1 + n_2 - 2$.

Zweistichproben-t-Test für ungleiche Varianzen (Welch-Test):

Verwende diesen Test, wenn die Varianzen deiner Populationen unterschiedlich sind.

Welch-Zweistichproben-t-Test mit ungleichen Varianzen:

wobei:

• $\Delta$ — der in der Nullhypothese angenommene Wert für die Differenz der Mittelwerte,
• $n_1$ — der Stichprobenumfang des ersten Datensatzes,
• $\bar{x}_1$ — der Mittelwert des ersten Datensatzes,
• $s_1$ — die Standardabweichung des ersten Datensatzes,
• $n_2$ — der Stichprobenumfang des zweiten Datensatzes,
• $\bar{x}_2$ — der Mittelwert des zweiten Datensatzes und
• $s_2$ — die Standardabweichung des zweiten Datensatzes.

Die Anzahl der Freiheitsgrade bei einem Welch-t-Test (Zweistichproben-t-Test mit ungleichen Varianzen) ist sehr schwer zu ermitteln. Wir können sie mithilfe der folgenden Satterthwaite-Gleichung annähern:

Alternativ kannst du auch den kleineren Wert aus $n_1 - 1$ und $n_2 - 1$ als angenäherten Schätzwert für die Anzahl der Freiheitsgraden nehmen.

Wenn wir Unterschiede in einer Population zwischen zwei verschiedenen Zeitpunkten untersuchen möchten, verwenden wir üblicherweise einen gepaarten t-Test. Die Population zum ersten Zeitpunkt kann als Vorgruppe bezeichnet werden, zum zweiten Zeitpunkt bezeichnen wir sie als Nachgruppe.

1. Mit der Nullhypothese behaupten wir, dass der wahre Unterschied zwischen den Mittelwerten der Vor- und der Nachpopulation gleich einer Prüfgröße, $\Delta$, ist.

2. Mit der Gegenhypothese wird behauptet, dass der tatsächliche Unterschied zwischen diesen Mittelwerten:

   • anders als $\Delta$ ist,
   • kleiner als $\Delta$ ist oder
   • größer als $\Delta$ ist.

Normalerweise ist die Prüfgröße gleich Null. Wir können die Hypothesen dann wie folgt umformulieren:

1. Mit der Nullhypothese wird behauptet, dass die Mittelwerte zu beiden Messzeitpunkten gleich sind, d. h. das Ereignis zwischen den beiden Zeitpunkten hat keinen Einfluss auf die Population.

2. Die Gegenhypothese:

   • die Mittelwerte vor und nach dem Ereignis unterscheiden sich voneinander (das Ereignis wirkt sich auf die untersuchten Parameter aus);
   • der Mittelwert vor dem Ereignis ist kleiner als der Mittelwert der zweiten Messung (Das Ereignis erhöht den untersuchten Wert) oder
   • der Mittelwert vor dem Ereignis ist größer als der Mittelwert der zweiten Messung (Das Ereignis verringert den untersuchten Wert).

Formel für den gepaarten t-Test

Ein gepaarter t-Test ist theoretisch gesehen dasselbe wie ein Einstichproben-t-Test! Schauen wir uns an, wieso: Seien $x_1, ..., x_n$ die Datenwerte zum ersten Messzeitpunkt und $y_1, ..., y_n$ die jeweiligen Datenwerte zum zweiten Messzeitpunkt. Das heißt, $x_i, y_i$ sind die Vorher- und Nachher-Messungen des i-ten Probanden.

Berechne nun für jeden Probanden die Differenz, $d_i := x_i - y_i$ Alles danach ist ein einfacher t-Test für die Stichprobe der Differenzen $d_1, ..., d_n$. Schauen wir uns die Formel für den t-Test-Wert an:

wobei:

• $\Delta$ — die in der Nullhypothese angenommene Differenz zwischen den Mittelwerten,

• $n$ — der Umfang der Differenzstichprobe, d. h. die Anzahl der Wertpaare,

• $\bar{x}$ — der Mittelwert der Stichprobenunterschiede und

• $s$ — die Standardabweichung der Stichprobenunterschiede.

Die Anzahl der Freiheitsgrade im gepaarten t-Test = $n - 1$

Wir verwenden einen Z-Test zur Ermittlung des Populationsmittelwertes eines normalverteilten Datensatzes mit bekannter Populationsvarianz. Je höher die Anzahl an Freiheitsgraden, desto mehr nähert sich die Student-t-Test-Verteilung der Normalverteilung N(0,1) an.

Wenn also viele Datenpunkte vorhanden sind (mindestens 30), kannst du anstatt des t-Tests einen Z-Test durchführen. Die Ergebnisse sind sich nahezu identisch. Denke jedoch daran, bei kleinen Stichproben mit unbekannter Varianz den t-Test zu verwenden, da die Student-t-Test-Verteilung in diesem Fall deutlich von der Normalverteilung N(0,1) abweicht!