Normalverteilung Rechner

Dieser Normalverteilung-Rechner berechnet die Fläche unter einer Glockenkurve und ermittelt die Wahrscheinlichkeit, dass ein Wert höher oder niedriger als ein beliebiger Wert X ist. Du kannst diesen Rechner auch verwenden, um die Wahrscheinlichkeit zu ermitteln, dass deine Variable in einem beliebigen Bereich von X bis X₂ liegt, indem du einfach den Mittelwert der Normalverteilung und die Standardabweichung einsetzt. Dieser Artikel erklärt die Grundbegriffe der Standard-Normalverteilung, gibt dir die Formel für die Verteilungsfunktion der Normalverteilung und liefert Beispiele für die Wahrscheinlichkeit der Normalverteilung.

Die Gaußsche Normalverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Die meisten Daten liegen in der Nähe eines zentralen Wertes, ohne dass sie nach links oder rechts abweichen. Viele Beobachtungen in der Natur, wie die Größe von Menschen oder der Blutdruck, folgen dieser Verteilung.

In einer Normalverteilung ist der Mittelwert auch der Median (die „mittlere“ Zahl einer sortierten Liste von Daten) und der Modus (der Wert mit der größten Häufigkeit). Da diese Verteilung symmetrisch um den Mittelpunkt ist, sind 50% der Werte niedriger als der Mittelwert und 50% der Werte höher als der Mittelwert.

Ein weiterer Parameter, der die Normalverteilung charakterisiert, ist die Standardabweichung 🇺🇸. Sie beschreibt, wie groß die Streuung der Zahlen ist. Im Allgemeinen sollten 68% der Werte innerhalb von einer Standardabweichung vom Mittelwert liegen, 95% innerhalb von 2 Standardabweichungen und 99,7% innerhalb von 3 Standardabweichungen. Die Anzahl der Standardabweichungen vom Mittelwert wird als z-Wert bezeichnet. Es kann sein, dass du zwar die Varianz, aber nicht die Standardabweichung deiner Verteilung kennst. Letztere lässt sich jedoch leicht ermitteln, indem du einfach die Quadratwurzel aus der Varianz ziehst.

Ein Anstieg des Mittelwerts verschiebt die gesamte Normalverteilung nach rechts. Eine Veränderung der Standardabweichung führt zu einer Verengung oder Streuung der Verteilung um den Mittelwert. Bei stark gestreuten Verteilungen ist es wahrscheinlicher, dass ein zufälliger Datenpunkt weit vom Mittelwert entfernt ist. Die Form der Kurve der Normalverteilung wird nur durch diese beiden Parameter bestimmt.

Du kannst jede Normalverteilung standardisieren, und zwar durch einen Prozess, der als Standardwert bekannt ist. Dabei subtrahierst du den Mittelwert der Grundgesamtheit vom Datenwert und teilst diese Differenz durch die Standardabweichung der Grundgesamtheit. Eine Standard-Normalverteilung hat die folgenden Eigenschaften:

• Der Mittelwert beträgt 0;
• Die Standardabweichung ist 1;
• Die Gesamtfläche unter der Kurve beträgt 1; und
• Jeder Wert der Variablen x wird in den entsprechenden z-Wert umgewandelt.

Du kannst dieses Tool auch mit dem Rechner für die Standard-Normalverteilung überprüfen. Wenn du den Mittelwert μ als 0 und die Standardabweichung σ als 1 eingibst, ist der z-Wert gleich X.

Die Gesamtfläche unter der Kurve der Standard-Normalverteilung beträgt 1. Das bedeutet, dass sie der Wahrscheinlichkeit entspricht. Die Wahrscheinlichkeit, dass dein Wert kleiner ist als ein beliebiger Wert X (bezeichnet als P(x < X)), kannst du als Fläche unter dem Graphen links neben dem z-Wert von X berechnen.

Schauen wir uns noch einmal das obige Diagramm an und betrachten die Verteilungswerte innerhalb einer Standardabweichung. Du kannst sehen, dass die verbleibende Wahrscheinlichkeit (0,32) aus zwei Regionen besteht. Die rechtsseitige und linksseitige Intervallgrenze der Normalverteilung sind symmetrisch und haben jeweils eine Fläche von 0,16. Das ist das Schöne der Mathematik und der Grund, warum Datenwissenschaftler die Gaußsche-Normalerteilung lieben!

Die Berechnung der Fläche unter dem Diagramm ist keine leichte Aufgabe. Du kannst entweder die Normalverteilungstabelle verwenden oder versuchen, die normale kumulative Verteilungsfunktion zu integrieren:

Nehmen wir zum Beispiel an, du möchtest die Wahrscheinlichkeit finden, dass eine Variable kleiner als $x$ ist. In diesem Fall solltest du diese Funktion von minus unendlich bis $x$ integrieren. Wenn du die Wahrscheinlichkeit finden möchtest, dass die Variable größer als $x$ ist, solltest du diese Funktion von $x$ bis unendlich integrieren. Weitere Informationen zu diesem Thema findest du im p-Wert Rechner.

Du kannst diesen Rechner auch als kumulativen Verteilungsfunktion-Rechner verwenden!

Beachte jedoch, dass die Verteilungsfunktion der Normalverteilung nicht mit ihrer Dichtefunktion (der Glockenkurve) verwechselt werden darf, die einfach allen Argumenten den Wahrscheinlichkeitswert zuweist:

Per Definition ist die Dichtefunktion die erste Ableitung, d. h. die Änderungsrate der Verteilungsfunktion.

1. Entscheide dich für den Mittelwert deiner Normalverteilung. Wir können zum Beispiel versuchen, die Verteilung der Körpergröße in Deutschland zu analysieren. Die durchschnittliche Größe eines erwachsenen Mannes beträgt 175,7 cm.

2. Wähle die Standardabweichung für deinen Datensatz. Nehmen wir an, sie ist 10 cm.

3. Angenommen, du möchtest diesen Normalverteilung-Rechner verwenden, um die Wahrscheinlichkeit zu bestimmen, dass ein Erwachsener größer als 185 cm ist. Dann wird dein $X$ 185 cm betragen.

4. Unser Normalverteilung-Rechner zeigt zwei Werte an: die Wahrscheinlichkeit, dass eine Person größer als 185 cm ($P(x > X)$) und kleiner als 185 cm ($P(x < X)$) ist. In diesem Fall beträgt der erste Wert 17,62% und der zweite 82,38%.

5. Du kannst auch die Option Erweiterter Modus des Rechners öffnen, um die Wahrscheinlichkeit zu berechnen, dass eine Variable $x$ in einem bestimmten Bereich liegt (von X bis X₂). Die Wahrscheinlichkeit, dass die Körpergröße eines erwachsenen deutschen Mannes zwischen 185 und 190 cm liegt, beträgt zum Beispiel 9,98%.

Die Normalverteilung beschreibt viele natürliche Phänomene: Prozesse, die kontinuierlich und in großem Maßstab ablaufen. Nach dem Gesetz der großen Zahlen liegt der Durchschnittswert eines ausreichend großen Stichprobenumfangs 🇺🇸, wenn er aus einer Verteilung gezogen wird, nahe am Mittelwert der zugrunde liegenden Verteilung. Je mehr Messungen du vornimmst, desto näher kommst du dem tatsächlichen Mittelwert der Grundgesamtheit.

Beachte jedoch, dass eine der robustesten statistischen Tendenzen die Rückläufigkeit zum Mittelwert ist. Dieser Begriff wurde vom berühmten britischen Wissenschaftler Francis Galton geprägt und erinnert uns daran, dass sich die Dinge im Laufe der Zeit angleichen. Größere Eltern neigen dazu, im Durchschnitt Kinder zu bekommen, deren Größe näher am Durchschnitt liegt. Nach einer Periode hohen Wachstums des Bruttoinlandsprodukts (BIP) neigt ein Land dazu, ein paar Jahre lang eine geringere Gesamtproduktion zu verzeichnen.

Es kommt häufig vor, dass die natürliche Variation in wiederholten Daten wie eine echte Veränderung aussieht. Es ist jedoch nur eine statistische Tatsache, dass auf relativ hohe (oder niedrige) Beobachtungen oft solche folgen, deren Werte näher am Durchschnitt liegen. Die Regression auf den Mittelwert ist oft die Quelle für anekdotische Hinweise, die wir statistisch nicht bestätigen können.

Die Normalverteilung ist für ihre mathematischen Wahrscheinlichkeiten bekannt. Verschiedene Wahrscheinlichkeiten, sowohl diskrete als auch kontinuierliche, tendieren dazu, gegen die Normalverteilung zu konvergieren. Das nennt man den Zentralen Grenzwertsatz, und er ist eindeutig einer der wichtigsten Sätze in der Statistik. Dank dieses Lehrsatzes kannst du mit dem Rechner für Mittelwert und Standardabweichung der Normalverteilung die Verteilung selbst der umfangreichsten Datensätze simulieren.

Je größer der Stichprobenumfang wird, desto mehr nähert sich der Mittelwert der Normalverteilung an, unabhängig von der ursprünglichen Form der Grundgesamtheit. Bei einer ausreichend großen Anzahl von Beobachtungen kann die Normalverteilung zum Beispiel zur Annäherung an die Poisson-Verteilung oder die Binomial-Wahrscheinlichkeitsverteilung verwendet werden. Daher betrachten wir die Normalverteilung oft als Grenzverteilung einer Folge von zufälligen Variablen.

Deshalb besagt die Best Practice, dass viele statistische Tests und Verfahren eine Stichprobe von mehr als 30 Datenpunkten benötigen, um sicherzustellen, dass eine Normalverteilung erreicht wird. In der Sprache der Statistik werden solche Eigenschaften oft als asymptotisch bezeichnet.

Wenn du dir nicht sicher bist, wie die zugrundeliegende Verteilung deiner Daten aussieht, du aber eine große Anzahl von Beobachtungen erhalten kannst, kannst du ziemlich sicher sein, dass sie der Normalverteilung folgen. Das gilt sogar für Random-Walk-Phänomene, also für Prozesse, die sich ohne erkennbares Muster oder einen Trend entwickeln.

Eine Tabelle der Standard-Normalverteilung, wie die untenstehende, ist gut, um die Referenzwerte bei der Erstellung von Konfidenzintervallen zu überprüfen. Du kannst unseren Normalverteilung-Rechner verwenden, um zu überprüfen, ob der Wert, den du für die Erstellung der Konfidenzintervalle verwendet hast, korrekt ist. Wenn zum Beispiel X = 1,96 ist, dann ist X der 97,5-Perzentilpunkt der Standard-Normalverteilung (setze den Mittelwert = 0, die Standardabweichung = 1 und X = 1,96. Du siehst, dass 97,5% der Werte unterhalb von X liegen).

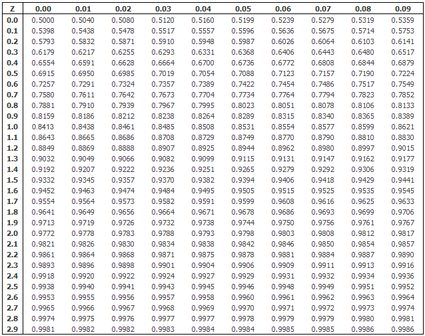
Wenn die von dir verwendete Beobachtung zufällig und unabhängig ist, sind auch der Mittelwert und die Varianz der Grundgesamtheit, die du aus der Stichprobe schätzt, unabhängig. Die univariate Gauß-Verteilung (berechnet für eine einzelne Variable) kann auch für eine Reihe von Variablen verallgemeinert werden. Eine spezielle „Summe“ namens Mehrdimensionale Normalverteilung zeigt die gemeinsame Verteilung einer bestimmten Anzahl von Variablen. Du kannst sie verwenden, um höherdimensionale Daten zu modellieren, z. B. eine umfassende Beurteilung von Patienten.

Statistiker gehen bei vielen Arten von statistischen Tests von der Annahme aus, dass die im Testverfahren verwendeten Beobachtungen der Gauß-Verteilung folgen. Sie gilt für fast alle Inferenzstatistiken, wenn du die Informationen der Stichprobe nutzt, um Verallgemeinerungen über die gesamte Population zu treffen.

Du kannst zum Beispiel formell prüfen, ob der geschätzte Wert eines Parameters statistisch von null verschieden ist oder ob ein Mittelwert in einer Grundgesamtheit gleich der anderen ist. Die meisten einfachen Tests, mit denen du solche Fragen beantworten kannst (die sogenannten parametrischen Tests), beruhen auf der Normalitätsannahme. Du kannst sie nicht anwenden, wenn eine empirische Verteilung andere Eigenschaften als eine Normalverteilung hat.

Du solltest diese Annahme überprüfen, bevor du diese Tests anwendest. Es gibt einige beliebte Normalitätstests, mit denen du feststellen kannst, ob deine Daten normal verteilt sind. Der Shapiro-Wilk-Test basiert auf der Varianz der Stichprobe. Im Gegensatz dazu basiert der Jarque-Bera-Test auf der Schiefe und der übermäßigen Kurtosis der empirischen Verteilung. Beide Tests ermöglichen dir eine genaue Interpretation und erhalten die Erklärungskraft statistischer Modelle.

Der Test auf Normalität hilft dir auch zu prüfen, ob du Überschussrenditen bei Finanzanlagen, wie z. B. Aktien, erwarten kannst oder wie gut dein Portfolio im Vergleich zum Markt abschneidet. Wir können den Mittelwert der empirischen Verteilung verwenden, um die Effektivität deiner Investition zu schätzen. Andererseits kannst du die Varianz verwenden, um das Risiko eines Portfolios zu bewerten.

Eine der am häufigsten verwendeten Normalitätsannahmen betrifft lineare (oder auch nichtlineare) Regressionsmodelle. In der Regel gehen wir davon aus, dass die Residuen des Schätzers der kleinsten Quadrate einer Normalverteilung mit einem Mittelwert von null und einer festen (zeitlich unveränderlichen) Standardabweichung folgen (du kannst dir diese Residuen als Abstand einer Regressionsgeraden zu den tatsächlichen Datenpunkten vorstellen). Du kannst die Anpassungsgüte des kleinsten quadratischen Modells mithilfe des Chi-Quadrat-Tests beurteilen. Wenn die Fehlerverteilung jedoch nicht normal ist, kann das bedeuten, dass deine Schätzungen verzerrt oder unwirksam sind.

Ein weiteres wichtiges Beispiel in diesem Bereich ist die ANOVA (Varianzanalyse), mit der überprüft werden kann, ob die Mittelwerte zweier Stichproben gleich sind. Die ANOVA kann auch in der kanonischen Form erfolgreich durchgeführt werden, wenn die Verteilung der Modellresiduen normal ist.

Es gibt mehrere Möglichkeiten, wie die Verteilung deiner Daten von der Normalverteilung abweichen kann, die beiden wichtigsten sind:

• Fat Tails (dicke Enden) — Extremwerte können mit höherer Wahrscheinlichkeit auftreten (d. h. es besteht eine relativ hohe Wahrscheinlichkeit, anormale Ergebnisse zu erhalten);
• Schiefe/Skewness — die Verteilung ist asymmetrisch. Der Mittelwert und der Median der Verteilung sind unterschiedlich (z. B. Streuung der Löhne auf dem Arbeitsmarkt).

Verteilungen, die nicht normalverteilt sind, sind in der Finanzwelt weit verbreitet, aber auch in der Psychologie oder in den Sozialwissenschaften kannst du mit solchen Problemen rechnen. Eines von vielen Beispielen für solche Verteilungen ist die geometrische Verteilung, die sich für die Modellierung einer Reihe unabhängiger Ereignisse eignet, z. B. das Ergebnis eines Würfelwurfs.

Die Gaußsche Normalverteilung ist eine glockenförmige Wahrscheinlichkeitsverteilung für unabhängige zufällige Variablen. Sie ist für die Statistik von entscheidender Bedeutung, weil sie die Verteilung der Werte für viele natürliche Phänomene genau beschreibt. Die Verteilungskurve ist symmetrisch um ihren Mittelwert, wobei sich die meisten Beobachtungen um eine zentrale Spitze gruppieren und die Wahrscheinlichkeiten für Werte, die weiter vom Mittelwert entfernt sind, in beiden Richtungen abnehmen.

Ja, eine Normalverteilung kann eine große Standardabweichung im Vergleich zum Mittelwert haben. Eine Normalverteilung kann zum Beispiel einen Mittelwert von 6 haben, aber eine Standardabweichung von 20. Im Allgemeinen gilt: Je breiter die Normalverteilung im Vergleich zum Mittelwert, desto größer ihre Standardabweichung.

Um festzustellen, ob ein Datensatz der Normalverteilung folgt:

1. Zeichne ein Diagramm der Datenverteilung.
2. Überprüfe, ob die Kurve die Form einer symmetrischen Glocke hat, die um den Mittelwert zentriert ist.
3. Prüfe die empirische Regel: 68% der Werte müssen innerhalb von einer Standardabweichung vom Mittelwert liegen, 95% innerhalb von 2 Standardabweichungen und 99,7% innerhalb von 3 Standardabweichungen.

Die beiden wichtigsten Parameter der Normalverteilung sind: der Mittelwert (μ) und die Standardabweichung (σ). μ bestimmt die Lage des Scheitelpunkts der Normalverteilung auf der numerischen Achse. σ ist ein Skalenparameter, der bewirkt, dass sich die Normalverteilung bei größeren Werten von σ stärker ausbreitet.

2,5%, wenn man davon ausgeht, dass bei einem Baum die Normalverteilung des Umfangs μ = 150 cm und σ = 30 cm beträgt.

1. Zeichne die Normalverteilung mit der Spitze bei μ = 150 cm und σ = 30 cm.
2. Beachte, dass der Umfang von 210 cm 2σ = 60 cm über dem Mittelwert liegt.
3. Nutze die empirische Regel, dass 95% der Daten innerhalb von ±2σ liegen.
4. Dividiere durch 2, um die Bäume mit einem Umfang über +2σ zu nehmen.