Z-Test Rechner

Mit diesem Z-Test-Rechner kannst du einen Einstichproben-Z-Test für den Mittelwert der Grundgesamtheit durchführen. Es gibt zwei Formen dieses Tests – einen zweiseitigen Z-Test und einen einseitigen Z-Test –, die du je nach deinen Bedürfnissen verwenden kannst. Du kannst auch wählen, ob der Rechner den p-Wert aus dem Z-Test ermitteln soll oder ob du lieber den Ansatz des kritischen Werts verwenden möchtest!

Lies weiter, um mehr über den Z-Test in der Statistik zu erfahren, insbesondere darüber, wann man Z-Tests verwendet, wie die Z-Test-Formel lautet und wann man den Z-Test oder den t-Test verwenden sollte. Wir zeigen dir zudem Schritt für Schritt, wie du Z-Tests durchführst!

Du kannst auch unseren t-Statistik Rechner benutzen, um das Konzept dieser wichtigen Statistik kennenzulernen. Wenn du dich für F-Tests interessierst, schau dir unseren F-Test Rechner 🇺🇸 an.

Der Z-Test mit einer Stichprobe ist einer der beliebtesten Zentralwert-Tests. Die Nullhypothese lautet, dass der Mittelwert der Grundgesamtheit gleich einer bestimmten Zahl ist, $\mu_0$:

Wir führen einen zweiseitigen Z-Test durch, wenn wir testen möchten, ob der Mittelwert der Grundgesamtheit nicht $\mu_0$ ist:

und ein einseitiger Z-Test, wenn wir prüfen möchten, ob der Mittelwert der Grundgesamtheit kleiner/größer als $\mu_0$ ist:

Lass uns nun die Annahmen eines Z-Tests mit einer Stichprobe besprechen.

Du kannst einen Z-Test verwenden, wenn deine Stichprobe aus unabhängigen Datenpunkten besteht und:

• die Daten normalverteilt sind und du die Varianz der Grundgesamtheit kennst;

  oder

• der Stichprobenumfang groß ist und die Daten einer Verteilung folgen, die einen endlichen Mittelwert und eine endliche Varianz hat. Du brauchst die Varianz der Grundgesamtheit nicht zu kennen.

Diese Voraussetzungen sind notwendig, um eine Test-Statistik zu erhalten, die der Normalverteilung $\mathrm N(0, 1)$ folgt. Im ersten Fall handelt es sich um eine exakte Normalverteilung, während sie im zweiten Fall wegen des zentralen Grenzwertsatzes nur angenähert ist.

Es stellt sich nur noch die Frage: „Wann gilt meine Stichprobe als groß?” Nun, es gibt keinen fixen Wert. Im Allgemeinen gilt: Je mehr Datenpunkte du hast, desto besser funktioniert die Annäherung. In Statistik-Lehrbüchern wird empfohlen, nicht weniger als 50 Datenpunkte zu haben, während 30 als das absolute Minimum gelten.

Sei $x_1, ..., x_n$ eine unabhängige Stichprobe, die der Normalverteilung $\mathrm N(\mu, \sigma^2)$ folgt, d. h. mit einem Mittelwert gleich $\mu$ und einer Varianz gleich $\sigma ^2$.

Wir stellen die Nullhypothese auf, $\mathrm H_0 \!\!:\!\! \mu = \mu_0$.

Wir definieren die Test-Statistik, Z, wie folgt:

wobei:

• $\bar x$ – der Stichprobenmittelwert ist, d. h. $\bar x = (x_1 + ... + x_n) / n$;

• $\mu_0$ – der in $\mathrm H_0$ postulierte Mittelwert ist;

• $n$ – der Stichprobenumfang ist; und

• $\sigma$ – die Standardabweichung der Grundgesamtheit ist.

Im Folgenden steht der Großbuchstabe $Z$ für die Test-Statistik (die als Zufallsvariable behandelt wird), während der Kleinbuchstabe $z$ einen tatsächlichen Wert von $Z$ bezeichnet, der für eine gegebene Stichprobe aus N(μ,σ²) berechnet wird.

Wenn $\mathrm H_0$ gilt, dann folgt die Summe $S_n = x_1 + ... + x_n$ der Normalverteilung mit dem Mittelwert $n \mu_0$ und der Varianz $n^2 \sigma$. Da $Z$ die Normierung (Z-Wert) von $S_n/n$ ist, können wir schlussfolgern, dass die Test-Statistik $Z$ der Standardnormalverteilung $\mathrm N(0, 1)$ folgt, vorausgesetzt, $\mathrm H_0$ ist wahr. Wir haben übrigens auch den Standardisierungsrechner | Z-Wert, wenn du dich nur auf diesen Wert konzentrieren möchtest.

Wenn unsere Daten nicht normalverteilt sind oder wenn die Standardabweichung der Grundgesamtheit nicht bekannt ist (und wir daher in der Formel für $Z$ die Standardabweichung der Grundgesamtheit $\sigma$ durch die Standardabweichung der Stichprobe ersetzen), dann ist die Test-Statistik $Z$ nicht unbedingt normal. Wenn die Stichprobe jedoch genügend groß ist, garantiert das zentrale Grenzwerttheorem, dass $Z$ ungefähr $\mathrm N(0, 1)$ ist.

In den folgenden Abschnitten erklären wir dir, wie du den Wert der Test-Statistik, $z$, verwenden kannst, um eine Entscheidung darüber zu treffen, ob du die Nullhypothese verwerfen solltest oder nicht. Für diese Entscheidung gibt es zwei Ansätze: den p-Wert-Ansatz und den Ansatz des kritischen Werts – wir schauen uns beide an! Welchen Ansatz solltest du verwenden? In der Vergangenheit war der Ansatz des kritischen Werts beliebter, weil es schwierig war, den p-Wert aus dem Z-Test zu berechnen. Mithilfe moderner Computer ist das heute jedoch relativ einfach und mit guter Genauigkeit möglich. Generell wird dir eher empfohlen, den p-Wert deiner Tests anzugeben!

Formal ist der p-Wert das kleinste Signifikanzniveau, bei dem die Nullhypothese verworfen werden kann. Intuitiver ausgedrückt, beantwortet der p-Wert die Frage:
Unter der Voraussetzung, dass ich in einer Welt lebe, in der die Nullhypothese gilt, wie wahrscheinlich ist es, dass der Wert der Test-Statistik mindestens so extrem ist wie der $z$-Wert, den ich für meine Stichprobe erhalten habe? Ein kleiner p-Wert bedeutet also, dass dein Ergebnis unter Annahme der Nullhypothese sehr unwahrscheinlich ist und es somit einen starken Beweis gegen die Nullhypothese gibt – je kleiner der p-Wert, desto stärker der Beweis.

Um den p-Wert zu ermitteln, musst du die Wahrscheinlichkeit berechnen, dass die Test-Statistik $Z$ mindestens so extrem ist wie der tatsächlich beobachtete Wert $z$, vorausgesetzt, die Nullhypothese ist wahr. Die Wahrscheinlichkeit ($W$) eines Ereignisses, die unter der Annahme berechnet wird, dass $\mathrm H_0$ wahr ist, wird als $\small \mathrm{W}(\text{Ereignis} | \mathrm{H_0})$ bezeichnet. Die Alternativhypothese legt fest, was extremer bedeutet:

1. Zweiseitiger Z-Test: Extremwerte sind diejenigen, deren absoluter Wert $|z|$ übersteigt, also kleiner als $-|z|$ oder größer als $|z|$ sind:

Die Symmetrie der Normalverteilung ergibt:

2. Linksseitiger Z-Test: Die Extremwerte sind kleiner als $z$, also

3. Rechtsseitiger Z-Test: Die Extremwerte sind größer als $z$, sind

Um diese Wahrscheinlichkeiten zu berechnen, können wir die Funktion der Standardnormalverteilung, Φ(x), von $\mathrm N(0, 1)$ verwenden, die für eine reelle Zahl, $x$, wie folgt definiert ist

Die p-Werte lassen sich auch gut als Fläche unter der Wahrscheinlichkeitsdichtefunktion von $\mathrm N(0, 1)$ darstellen, denn:

Mit all dem Wissen aus dem vorherigen Abschnitt bist du nun gut gerüstet, um dein Verständnis für Z-Tests weiter zu vertiefen.

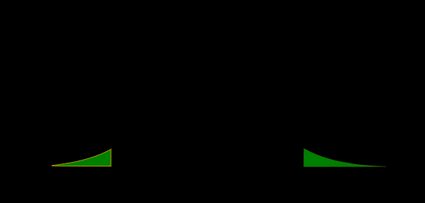
1. Zweiseitiger Z-Test:

Aus der Tatsache, dass $\Phi(-z) = 1 - \Phi(z)$, leiten wir ab, dass

Der p-Wert ist die Fläche unter der Wahrscheinlichkeitsverteilung, sowohl links von $-|z|$ als auch rechts von $|z|$:

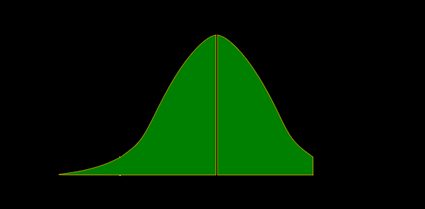
2. Linksseitiger Z-Test:

Der p-Wert ist die Fläche unter der Wahrscheinlichkeitsverteilung links von $z$:

3. Rechtsseitiger Z-Test:

Der p-Wert ist die Fläche unter der Wahrscheinlichkeitsverteilung rechts von $z$:

Die Entscheidung, ob du die Nullhypothese verwerfen solltest oder nicht, kannst du nun auf einem beliebigen Signifikanzniveau, $\alpha$, treffen!

• Wenn der p-Wert kleiner oder gleich $\alpha$ ist, wird die Nullhypothese auf diesem Signifikanzniveau verworfen.

• Wenn der p-Wert größer ist als $\alpha$, dann gibt es nicht genug Beweise, um die Nullhypothese auf diesem Signifikanzniveau zu verwerfen.

Bei der Methode der kritischen Werte wird der Wert der Test-Statistik, den wir für unsere Stichprobe $z$ erhalten haben, mit den sogenannten kritischen Werten verglichen. Diese Werte bilden die Grenzen der Regionen, in denen die Test-Statistik höchstwahrscheinlich liegt. Diese Regionen werden als kritischer Bereich oder Ablehnungsbereich bezeichnet. Die Entscheidung, ob du die Nullhypothese ablehnen solltest oder nicht, hängt also davon ab, ob unsere $z$ im Ablehnungsbereich liegt oder nicht.

Die kritischen Bereiche hängen von einem Signifikanzniveau, $\alpha$, des Tests und von der Alternativhypothese ab. Die Wahl von $\alpha$ ist willkürlich; in der Praxis werden meist die Werte 0,1, 0,05 oder 0,01 als $\alpha$ verwendet.

Sobald wir uns auf den Wert von $\alpha$ geeinigt haben, können wir die kritischen Bereiche des Z-Tests leicht bestimmen:

1. Zweiseitiger Z-Test:

2. Linksseitiger Z-Test:

3. Rechtsseitiger Z-Test:

Um über $\mathrm H_0$ zu entscheiden, prüfst du, ob dein $z$ in den kritischen Bereich fällt oder nicht:

• Wenn ja, dann lehne $\mathrm H_0$ ab und akzeptiere $\mathrm H_1$.

• Wenn nicht, dann gibt es nicht genug Beweise, um $\mathrm H_0$ abzulehnen.

Wie du siehst, beinhalten die Formeln für die kritischen Werte von Z-Tests den Kehrwert, $\Phi^{-1}$, der Standardnormalverteilung.

Unser Rechner vereinfacht alle komplizierten Schritte:

1. Wähle die Alternativhypothese: zweiseitig oder links-/rechtsseitig.

2. In unserem Z-Test-Rechner kannst du entscheiden, ob du den p-Wert oder den Ansatz des kritischen Bereichs verwenden möchtest. In letzterem Fall legst du das Signifikanzniveau, $\alpha$, fest.

3. Gib den Wert der Test-Statistik ein, $z$. Wenn du ihn nicht kennst, kannst du einige Daten eingeben, mit denen wir dein $z$ für dich berechnen können:

   • Stichprobenmittelwert $\bar x$ (wenn du Rohdaten hast, gehe zum Arithmetisches Mittel Rechner, um den Mittelwert zu ermitteln);
   • angenommener Mittelwert der Nullhypothese $\mu_0$;
   • Stichprobenumfang $n$; und
   • Standardabweichung der Grundgesamtheit $\sigma$ (oder Standardabweichung der Stichprobe, wenn deine Stichprobe groß ist).

4. Die Ergebnisse werden direkt unterhalb des Rechners angezeigt.

Wenn du $z$ anhand des p-Wertes finden möchtest, bedenke bitte, dass es bei zweiseitigen Tests zwei mögliche Werte von $z$ gibt: einen positiven und einen negativen, und zwar die entgegengesetzten Zahlen. Dieser Z-Test-Rechner liefert in einem solchen Fall den positiven Wert. Um den anderen möglichen Wert von $z$ für einen bestimmten p-Wert zu ermitteln, nimm einfach die negative Zahl von diesem Wert.

Gehen wir einige Beispiele durch, um sicherzugehen, dass du das Wesentliche des Z-Tests verstanden hast:

1. Eine Flaschenabfüllmaschine folgt einer Normalverteilung. Ihre Standardabweichung beträgt nach Angaben des Herstellers 30 ml. Ein Saftverkäufer behauptet, dass das Volumen, das in jede Flasche gefüllt wird, im Durchschnitt einen Liter, also 1000 ml, beträgt, aber wir vermuten, dass das durchschnittliche Volumen in Wirklichkeit kleiner ist...

Die Hypothesen, die wir aufstellen, sind die folgenden:

• $\mathrm H_0 \! : \mu = 1000 \text{ ml}$

• $\mathrm H_1 \! : \mu \lt 1000 \text{ ml}$

Wir sind in ein Geschäft gegangen und haben 9 Flaschen (= Stichprobenumfang) gekauft. Nachdem wir die Saftmenge in jeder Flasche sorgfältig abgemessen hatten, erhielten wir die folgenden Werte (in Millilitern):

$\small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980$.

• Stichprobenumfang: $n = 9$;

• Mittelwert der Stichprobe: $\bar x = 980 \ \mathrm{ ml}$;

• Standardabweichung der Stichprobe: $\sigma = 30 \ \mathrm{ ml}$;

• also:

• Und deshalb: $\text{p-Wert} = \Phi(-2) \approx 0,\!0228$.

  Da $0,\!0228 \lt 0,\!05$ kommen wir zu dem Schluss, dass unser Verdacht nicht unbegründet ist; beim häufigsten Signifikanzniveau von 0,05 würden wir die Behauptung des Herstellers, $\mathrm H_0$, ablehnen, und die Alternativhypothese, $\mathrm H_1$, akzeptieren.

2. Wir haben 50 Mal eine Münze geworfen. Wir haben 20 Mal Zahl und 30 Mal Kopf erhalten. Gibt es genügend Beweise, um zu behaupten, dass die Münze manipuliert ist?

   Unsere Daten folgen eindeutig der Bernoulli-Verteilung, mit einer gewissen Erfolgswahrscheinlichkeit $p$ und einer Varianz $\sigma^2 = p (1-p)$. Die Stichprobe ist jedoch groß, sodass wir einen Z-Test durchführen können. Wir nehmen an, dass es ein Erfolg ist, wenn die Münze auf Zahl fällt.

   Stellen wir die Nullhypothese und die Alternativhypothese auf:

   • $\mathrm H_0 \! : p = 0,\!5$ (die Münze ist fair – die Wahrscheinlichkeit, dass Zahl fällt, ist $0,\!5$); und

   • $\mathrm H_1 \! : p \ne 0,\!5$ (die Münze ist verzerrt – die Wahrscheinlichkeit, Zahl zu werfen ist anders als $0,\!5$).

In unserer Stichprobe haben wir 20 Erfolge (gekennzeichnet durch Einsen) und 30 Misserfolge (gekennzeichnet durch Nullen), also:

• Stichprobenumfang $n = 50$;

• Mittelwert der Stichprobe $\bar x = 20/50 = 0,\!4$;

• Die Standardabweichung der Grundgesamtheit ist durch $\sigma = \sqrt{0,\!5 \times 0,\!5}$ gegeben (weil $0,\!5$ der Anteil $p$ ist, der in $\mathrm H_0$ angenommen wurde). Daraus folgt: $\sigma = 0,\!5$;

• also

• und, deshalb:

Da $0,\!1573 \gt 0,\!1$ haben wir nicht genug Beweise, um die Behauptung zu verwerfen, dass die Münze fair ist, selbst bei einem so hohen Signifikanzniveau wie $0,\!1$. In diesem Fall kannst du sie getrost deinem Hexer zuwerfen oder den Münzwurf Wahrscheinlichkeit Rechner benutzen, um die Wahrscheinlichkeit zu ermitteln, dass du z. B. 10 Mal hintereinander Kopf wirfst (die extrem gering ist!).