Oberflächen Rechner

Dieser Oberflächen-Rechner hilft dir, den Flächeninhalt der gängigsten dreidimensionalen Körper zu bestimmen. Wenn du dich schon immer gefragt hast, wie der Flächeninhalt bestimmt wird oder wie groß die Oberfläche eines Körpers ist, hilft dir dieser Rechner weiter. Der Flächeninhalt hat eine riesige Liste von Anwendungen in allen Bereichen, z. B. in der Aerodynamik, Molekularbiologie und Chemie.

In diesem Artikel findest du die Formeln für den Flächeninhalt von Kugeln, Würfeln, Quadern, Zylindern, Pyramiden, Kegeln und Dreiecksprismen. Wir erklären dir zudem beispielhaft die Berechnung des Flächeninhalts einer Kugel.

Der Flächeninhalt ist die gesamte Fläche, die die Oberfläche des Objekts einnimmt.

Manchmal wird der Flächeninhalt auch in eine Summe aus Grundfläche(n) und Seitenfläche aufgeteilt. Die Seitenfläche ist der Flächeninhalt aller Seiten des Objekts, mit Ausnahme der Grund- und Deckfläche. Diese Unterteilung wird für Formen verwendet, bei denen es eine offensichtliche Unterscheidung zwischen der Grundfläche und dem anderen Teil gibt – z. B. bei Zylindern, Kegeln, Pyramiden oder Dreiecksprismen. Sie wird selten auf Körper angewendet, bei denen wir nicht sicher sind, welche Flächen als Grundflächen zu behandeln sind (wie bei Würfeln), und wir verwenden sie nicht für Körper mit durchgehend glatten Oberflächen wie Kugeln.

Mit unserem Oberflächen-Rechner kannst du den Flächeninhalt von sieben verschiedenen Festkörpern berechnen. Die Formel hängt von der Art des Festkörpers ab.

• Flächeninhalt einer Kugel: A = 4πr², wobei r für den Radius der Kugel steht.

• Flächeninhalt eines Würfels: A = 6a², wobei a die Seitenlänge ist.

• Flächeninhalt eines Zylinders: A = 2πr² + 2πrh, wobei r der Radius und h die Höhe des Zylinders ist.

• Flächeninhalt eines Kegels: A = πr² + πr√(r² + h²), wobei r der Radius und h die Höhe des Kegels ist.

• Flächeninhalt eines rechteckigen Prismas (Quaders): A = 2(ab + bc + ac), wobei a, b und c die Längen der drei Seiten des Quaders sind.

• Flächeninhalt eines Dreiecksprismas: A = 0,5 ∙ √((a + b + c) ∙ (-a + b + c) ∙ (a - b + c) ∙ (a + b - c)) + h ∙ (a + b + c), wobei a, b und c die Längen der drei Seiten der Grundfläche sind und h die Höhe (Länge) des Prismas ist.

• Flächeninhalt einer Pyramide: A = l ∙ √(l² + 4 ∙ h²) + l², wobei l eine Seitenlänge der quadratischen Grundfläche und h eine Höhe der Pyramide ist.

Aber woher kommen diese Formeln? Wie kann man den Flächeninhalt dieser dreidimensionalen Grundformen bestimmen? Lies weiter, und du wirst es herausfinden!

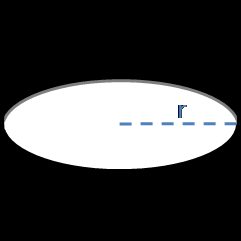
Um den Flächeninhalt einer Kugel zu berechnen, musst du nur ihren Radius oder Durchmesser kennen.

• A = 4 ∙ π ∙ r², wobei r der Radius ist.

Da wir wissen, dass der Durchmesser einer Kugel das Doppelte des Radius ist (d = 2r), können wir die Gleichung auch folgendermaßen schreiben:

• A = 4 ∙ π ∙ (d / 2)² = π ∙ d², wobei d der Kugeldurchmesser ist.

Für die Herleitung dieser Formel für den Flächeninhalt musst du das Integral bilden. Wenn du neugierig bist, schau dir diesen Beweis auf Englisch oder diesen Beweis auf Deutsch an.

Um den Flächeninhalt eines Zylinders zu ermitteln, brauchst du zwei Werte: den Radius (oder Durchmesser) einer Grundfläche und die Höhe des Zylinders. Die allgemeine Gleichung lautet Radius mal Höhe. Im Fall des Zylinders ist ein Kreis die Grundfläche.

• A = 2πr² + 2πrh

Woher kommt diese Formel? Du kannst die Gleichung für den Flächeninhalt eines Zylinders wie folgt herleiten:

• A = A(Seitenfläche) + 2 ∙ A(Grundfläche)

Es ist einfach, den Flächeninhalt zu bestimmen — wir erinnern uns an die bekannte Formel für den Flächeninhalt eines Kreises: A(Basis) = π ∙ r². Aber wie sieht es mit den Seitenflächen aus? Stell dir vor, wir sie „falten sie auf“. Erkennst du die Form? Es ist ein Rechteck! Die eine Seitenlänge ist die Höhe des Zylinders und die zweite ist der entfaltete Kreisumfang.

• A(Basis) = π ∙ r²
• A(Seitenfläche) = h ∙ (2 ∙ π ∙ r)

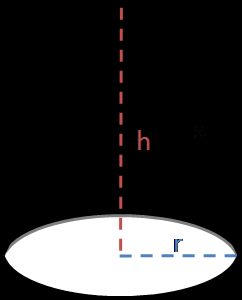
Wir können den Flächeninhalt eines Kegels in zwei Teile aufteilen:

• A = A(Seitenfläche) + A(Grundfläche), da wir im Gegensatz zum Zylinder nur eine Basis haben.

Die Grundfläche ist wiederum der Flächeninhalt eines Kreises A(Grundfläche) = π ∙ r², aber der Ursprung der Seitenfläche ist vielleicht nicht so offensichtlich:

• A(Seitenfläche) = π ∙ r ∙ √(r² + h²).

Schauen wir uns schrittweise die Herleitung an:

1. Rolle die Seitenfläche flach aus. Sie ergibt einen Kreissektor, also der Teil eines Kreises mit dem Radius s (s ist die Schräghöhe des Kegels).

2. Für den Kreis mit dem Radius s gilt: der Umfang ist gleich 2 ∙ π ∙ s. Die Bogenlänge des Sektors ist gleich 2 ∙ π ∙ r.

3. Der Flächeninhalt eines Sektors — also die Seitenfläche eines Kegels — ergibt sich aus der Formel:

• A(Seitenfläche) = (s ∙ (Bogenlänge)) / 2 = (s ∙ 2 ∙ π ∙ r) / 2 = π ∙ r ∙ s.

  Die Formel lässt sich aus den Proportionen ableiten, denn das Verhältnis der Flächeninhalte der Formen ist dasselbe wie das Verhältnis der Bogenlänge zum Umfang:

  (Sektorfläche) / (Kreisfläche) = (Bogenlänge) / (Kreisumfang) also:

  (Sektorfläche) / (π ∙ s²) = (2 ∙ π ∙ r) / (2 ∙ π ∙ s)

  (Flächeninhalt des Sektors) = (π ∙ s²) ∙ (2 ∙ π ∙ r) / (2 ∙ π ∙ s)

• A(Seitenfläche) = π ∙ r ∙ s

  Um den fehlenden Term dieses Verhältnisses zu finden, kannst du auch unseren Quotientenrechner 🇺🇸 ausprobieren!

4. Normalerweise haben wir nicht den Wert s, sondern h, die Höhe des Kegels gegeben, aber das ist überhaupt kein Problem! Wir können die Formel ganz einfach mit dem Satz des Pythagoras umformen:

• r² + h²= s². Wenn wir die Quadratwurzel ziehen, erhalten wir s = √(r² + h²)

  Die Formel für den Flächeninhalt der Seitenfläche sieht also wie folgt aus:

• A(Seitenfläche) = π ∙ r ∙ √(r² + h²)

5. Addiere schließlich die Flächeninhalte der Grundfläche und der Seitenfläche zusammen, um die endgültige Formel für den Flächeninhalt eines Kegels zu erhalten:

• A = A(Seitenfläche) + A(Grundfläche) = π ∙ r ∙ s + π ∙ r² mit r und s oder
• A = π ∙ r ∙ √(r² + h²) + π ∙ r² mit r und h.

Der Flächeninhalt eines Würfels 🇺🇸 ist die einfachste Berechnung, die du dir vorstellen kannst: Jede der Seiten ist ein Quadrat! Da jeder Würfel sechs gleiche quadratische Seiten hat, ist der Flächeninhalt gleich:

• A = 6 ∙ (Flächeninhalt der Seiten)

Da der Flächeninhalt eines Quadrats das Produkt der Länge seiner Seiten ist, lautet die endgültige Formel für den Flächeninhalt eines Würfels:

• A = 6 ∙ l², wobei l eine Quadratseite ist.

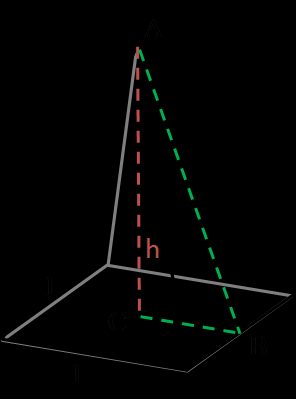
Eine Pyramide ist ein dreidimensionaler Körper mit einer polygonalen Basis und dreieckigen Seitenflächen. Wenn man das Wort Pyramide hört, wird normalerweise angenommen, dass es sich um eine regelmäßige quadratische Pyramide handelt (siehe Abbildung). Aber je nach Form der Grundfläche kann es sich auch um eine sechseckige oder rechteckige Pyramide handeln. Regelmäßig bedeutet, dass sie eine regelmäßige Polygonbasis hat und senkrecht ist (der Scheitelpunkt ist direkt über dem Schwerpunkt der Basis), und rechteckig bedeutet, dass sie diese Form als Basis hat. Das ist die Option, die wir als Pyramide in diesem Oberflächen-Rechner verwenden.

Die Formel für den Flächeninhalt einer Pyramide lautet:

• A = l ∙ √(l² + 4 ∙ h²) + l², wobei l die Grundseite und h die Höhe der Pyramide ist.

Auch hier können wir die Gleichung aufteilen in:

A = A(Grundfläche) + A(Seitenfläche) = A(Basis) + 4 ∙ A(Seitenfläche)

Die Grundfläche hat die Form eines Quadrats, also ist A(Grundfläche) = l². Um den Flächeninhalt der Seitenfläche zu berechnen, gehen wir von dem Flächeninhalt einer Dreiecksfläche aus:

1. Um die Höhe des Dreiecks zu ermitteln, verwenden wir wieder die Formel für die Hypotenuse:

   c = √(a² + b²)

2. Berechne die Hypotenuse des Dreiecks ABC (die gleichzeitig auch die Höhe der Dreiecksfläche ist):

   c = √(h² + (l/2)²) = √(h² + l²/4).

3. Der Flächeninhalt eines Dreiecks (in unserem Fall ist es ein gleichschenkliges Dreieck) kann wie folgt berechnet werden:

   A = Höhe ∙ Grundfläche / 2, also
   A(Seitenfläche) = √(h² + l²/4) ∙ l / 2.

4. Die endgültige Formel für den Flächeninhalt einer Pyramide lautet also:

   A = l² + 4 ∙ √(h² + l²/4) ∙ l / 2 = l² + 2 ∙ l ∙ √(h² + l²/4)

   A = l² + l ∙ √(4 ∙ h² + l²)

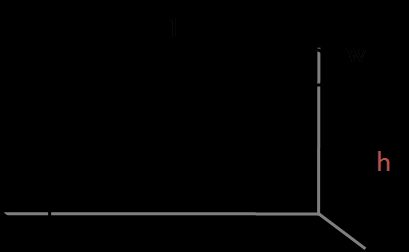
Um den Flächeninhalt eines rechteckigen Prismas bzw. Quaders zu berechnen, musst du nur die Flächeninhalte der rechteckigen Seiten berechnen:

• A = 2 ∙ (A1 + A2 + A3),

wobei:

• A1 = l ∙ b,
• A2 = b ∙ h und
• A3 = l ∙ h.

Die endgültige Formel lautet also:

• A = 2 ∙ (l ∙ b + b ∙ h + l ∙ h).

Um zu verstehen, woher die Formel für den Flächeninhalt eines Dreiecksprismas kommt, schauen wir uns die Herleitung an:

1. Der Flächeninhalt der Seitenflächen ist in diesem Fall leicht zu berechnen. Wie du auf dem Bild sehen kannst, besteht es aus drei Rechtecken mit einer gemeinsamen Seitenlänge:

   A(Seitenfläche) = a ∙ h + b ∙ h + c ∙ h = h ∙ (a + b + c)

   was wir auch in Kurzform schreiben können als:

   A(Seitenfläche) = h ∙ U, wobei U der Umfang eines Grunddreiecks ist.

2. Bestimme dann den Flächeninhalt einer dreieckigen Grundfläche. Das kannst du auf viele Arten tun, je nachdem, was du zur Verfügung hast. In unserem Rechner haben wir die Berechnung nach dem Satz des Heron 🇺🇸 implementiert — sie wird verwendet, wenn du drei Dreiecksseiten gegeben hast (SSS).

   A(Grundfläche) = 0,25 ∙ √((a + b + c) ∙ (-a + b + c) ∙ (a - b + c) ∙ (a + b - c)))

3. Die endgültige Formel für den Flächeninhalt eines dreieckigen Prismas lautet also:

   A = A(Seitenfläche) + 2 ∙ A(Grundfläche) bzw.

   A = h ∙ (a + b + c) + 0,5 ∙ √((a + b + c) ∙ (-a + b + c) ∙ (a - b + c) ∙ (a + b - c))

Du kannst die Oberfläche jedes unregelmäßigen Körpers berechnen, zum Beispiel auch die deines Körpers. Wenn du wissen möchtest, wie groß der Flächeninhalt eines menschlichen Körpers ist, schau dir unseren BSA Rechner − Körperoberfläche an.

Um den Flächeninhalt einer Kugel zu berechnen, befolge diese Schritte:

1. Bestimme den Radius der Kugel. Nehmen wir einen Radius von 10 cm.

2. Setze diesen Wert in die Formel ein:

   A = 4πr²

3. Berechne das Ergebnis:

   A = 4π ∙ 10² = 1256 cm²

4. Wenn du den Flächeninhalt der Kugel kennst, kannst du auch einen Onlinerechner verwenden, um den Radius der Kugel zu ermitteln.

Die Einheiten des Flächeninhalts sind immer quadratische Längeneinheiten. Du kannst sie zum Beispiel in cm², in², ft², m² oder Hektar angeben.

Wenn du das Volumen einer dieser Flächeneinheiten ermitteln möchtest, verwende unseren Volumen Rechner.

Um die Seitenlänge eines Würfels aus dem Flächeninhalt zu berechnen, gehst du folgendermaßen vor:

1. Schreibe den Flächeninhalt deines Würfels auf.
2. Dividiere ihn durch sechs. Das Ergebnis ist der Flächeninhalt einer Seite.
3. Ziehe die Quadratwurzel aus dem Ergebnis aus Schritt 2.
4. Das ist die Länge jeder Seite deines Würfels. Gut gemacht!

Um den Radius einer Kugel aus ihrem Flächeninhalt herzuleiten:

1. Schreibe den Flächeninhalt der Kugel auf.
2. Dividiere ihn durch 4π ≈ 12,566.
3. Ziehe die Quadratwurzel: √(Flächeninhalt / 4π).
4. Das war's; das ist der Radius! Du kannst dein Ergebnis mit einem Online-Rechner für den Flächeninhalt überprüfen.

Die Antwort lautet 50,2655 cm². Um dieses Ergebnis abzuleiten, werfe einen Blick auf die Formel für den Flächeninhalt eines Zylinders:

Flächeninhalt = 2πr(r + h).

Setzt man nun r = h = 2 ein, erhält man den Flächeninhalt 16π ≈ 50,2655. Denke an die Einheiten! Da sowohl r als auch h in cm angegeben sind, wird der Flächeninhalt in in cm² angegeben.